ОСНОВЫ ПРОГРАММИРОВАНИЯ_2014. Учебное пособие для 1го курса оглавление Оглавление 2 основы программирования 2 Введение 2
 Скачать 4.81 Mb. Скачать 4.81 Mb.
|
1. ОСНОВЫ АЛГОРИТМИЗАЦИИ1.1. Алгоритмы и величиныЭтапы решения задачи на ЭВМ. Работа по решению любой задачи с использованием компьютера делится на следующие этапы:
Часто эту последовательность называют технологической цепочкой решения задачи на ЭВМ. Непосредственно к программированию в этом списке относятся пункты 3, 4, 5. На этапе постановки задачи должно быть четко сформулировано, что дано и что требуется найти. Здесь очень важно определить полный набор исходных данных, необходимых для получения решения. Второй этап — формализация задачи. Здесь чаще всего задача переводится на язык математических формул, уравнений, отношений. Если решение требует математического описания какого-то реального объекта, явления или процесса, то формализация равносильна получению соответствующей математической модели. Третий этап — построение алгоритма. Опытные программисты часто сразу пишут программы на языках, не прибегая к каким-либо специальным способам описания алгоритмов (блок-схемам, псевдокодам). Однако в учебных целях полезно использовать эти средства, а затем переводить полученный алгоритм на язык программирования. Первые три этапа предусматривают работу без компьютера. Дальше следует собственно программирование на определенном языке, в определенной системе программирования. Последний (шестой) этап — это использование уже разработанной программы в практических целях. Таким образом, программист должен обладать следующими знаниями и навыками:
Основой программистской грамотности является развитое алгоритмическое мышление. Понятие алгоритма. Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithm! — латинского написания имени Мухаммеда аль-Хорезми (787—850), выдающегося математика средневекового Востока. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами. Сложение, вычитание, умножение столбиком, деление уголком многозначных чисел — вот первые алгоритмы в математике. Правила алгебраических преобразований, способы вычислений корней уравнений также можно отнести к математическим алгоритмам. В наше время понятие алгоритма трактуется шире. Алгоритм — это последовательность команд управления каким-либо исполнителем. В школьном курсе информатики с понятием алгоритма, с методами построения алгоритмов ученики знакомятся на примерах учебных исполнителей: Робота, Черепахи, Чертежника и т.д. Эти исполнители ничего не вычисляют. Они создают рисунки на экране, перемещаются в лабиринтах, перетаскивают предметы с места на место. Таких исполнителей принято называть исполнителями, работающими в обстановке. В разделе информатики под названием «Программирование» изучаются методы программного управления работой ЭВМ. Следовательно, в качестве исполнителя выступает компьютер. Компьютер работает с величинами — различными информационными объектами: числами, символами, кодами и т. п. Поэтому алгоритмы, предназначенные для управления компьютером, принято называть алгоритмами работы с величинами. Данные и величины. Совокупность величин, с которыми работает компьютер, принято называть данными. По отношению к программе данные делятся на исходные, результаты (окончательные данные) и промежуточные (рис. 1), которые получаются в процессе вычислений.  Например, при решении квадратного уравнения ax2 + bx + с = 0 исходными данными являются коэффициенты а, b, с, результатами — корни уравнения х1, х2, промежуточным данным — дискриминант уравнения D = b2 — 4aс. Для успешного освоения программирования необходимо усвоить следующее правило: всякая величина занимает свое определенное место в памяти ЭВМ (иногда говорят — ячейку памяти). Хотя термин «ячейка» с точки зрения архитектуры современных ЭВМ несколько устарел, однако в учебных целях его удобно использовать. У всякой величины имеются три основных свойства: имя, значение и тип. На уровне команд процессора величина идентифицируется при помощи адреса ячейки памяти, в которой она хранится. В алгоритмах и языках программирования величины делятся на константы и переменные Константа — неизменная величина, и в алгоритме она представляется собственным значением, например: 15, 34.7, k, true и т.д. Переменные величины могут изменять свои значения в ходе выполнения программы и представляются символическими именами — идентификаторами, например: X, S2, codl5. Любая константа, как и переменная, занимает ячейку памяти, а значение этих величин определяется двоичным кодом в этой ячейке. Теперь о типах величин — типах данных. С понятием типа данных вы уже, возможно, встречались, изучая в курсе информатики базы данных и электронные таблицы. Это понятие является фундаментальным для программирования. В каждом языке программирования существует своя концепция типов данных, своя система типов. Тем не менее в любой язык входит минимально необходимый набор основных типов данных, к которому относятся: целый, вещественный, логический и символьный типы. С типом величины связаны три ее характеристики: множество допустимых значений, множество допустимых операций, форма внутреннего представления. В табл. 1.1 представлены эти характеристики основных типов данных. Таблица 1.1  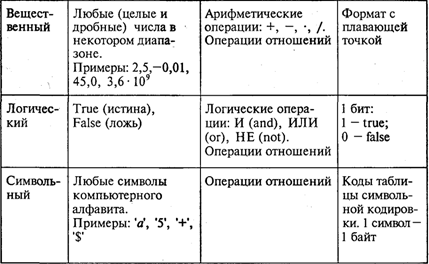 Типы констант определяются по контексту (т. е. по форме записи в тексте), а типы переменных устанавливаются в описаниях переменных. Есть еще один вариант классификации данных — классификация по структуре. Данные делятся на простые и структурированные. Для простых величин (их еще называют скалярными) справедливо утверждение: одна величина — одно значение, для структурированных: одна величина — множество значений. К структурированным величинам относятся массивы, строки, множества и т.д. ЭВМ — исполнитель алгоритмов. Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя в рамках его системы команд. О каком же исполнителе идет речь при обсуждении вопроса о программировании для ЭВМ? Ответ очевиден: исполнителем является компьютер. Точнее говоря, исполнителем является комплекс ЭВМ + Система программирования (СП). Программист составляет программу на том языке, на который ориентирована СП. Иногда в литературе такой комплекс называют виртуальной ЭВМ. Например, компьютер с работающей системой программирования на Бэйсике называют Бэйсик-машиной; компьютер с работающей системой программирования на Паскале называют Паскаль-машиной и т.п. Схематически это изображено на рис. 2. 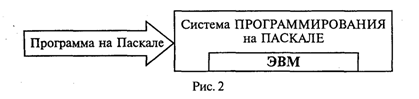 Входным языком такого исполнителя является язык программирования Паскаль. Независимо от того, на каком языке программирования будет написана программа, алгоритм решения любой задачи на ЭВМ может быть составлен из команд:
1.2. Линейные вычислительные алгоритмыОсновным элементарным действием в вычислительных алгоритмах является присваивание значения переменной величине. Если значение константы определено видом ее записи, то переменная величина получает конкретное значение только в результате присваивания. Присваивание может осуществляться двумя способами: с помощью команды присваивания и с помощью команды ввода. Формат команды присваивания следующий: переменная:=выражение Знак «:=» нужно читать как «присвоить». Команда присваивания обозначает следующие действия, выполняемые компьютером:
В описаниях алгоритмов необязательно соблюдать строгие правила в записи выражений. Их можно писать в обычной математической форме. Это еще не язык программирования со строгим синтаксисом. Обычно с помощью команды ввода присваиваются значения исходных данных, а команда присваивания используется для получения промежуточных и конечных величин. Полученные компьютером результаты решения задачи должны быть сообщены пользователю. Для этих целей предназначена команда вывода. С помощью этой команды результаты выводятся на экран или на устройство печати на бумагу. Поскольку присваивание является важнейшей операцией в вычислительных алгоритмах, обсудим ее более подробно. Определим три основных свойства команды присваивания:
1.3. Ветвления и циклы в вычислительных алгоритмахСоставим алгоритм решения квадратного уравнения Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты а, b, с. Решением в общем случае будут два корня x1 и х2, которые вычисляются по формуле: Все используемые в этой программе величины вещественного типа.  Слабость такого алгоритма видна невооруженным глазом. Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам, — универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и завершать работу. Результатом может быть число, но может быть и сообщение о том, что при определенных данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Упомянутое свойство в литературе по программированию называют результативностью алгоритма (в любом случае должен быть получен какой-то результат). Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи. Решение уравнения зависит от значений коэффициентов a, b, с. Вот анализ рассмотренной выше задачи (ограничиваемся только поиском вещественных корней): если a = 0, b = 0, с = 0, то любое х — решение уравнения; если а = 0,b = 0, с ≠ 0,то уравнение действительных решений не имеет; если а = 0, b ≠ 0, то это линейное уравнение, которое имеет одно решение х = -с/b; если a ≠ 0 и d = b2- 4ас ≥ 0, то уравнение имеет два вещественных корня (формулы приведены выше); если а ≠ 0 и d < 0, то уравнение не имеет вещественных корней. Блок-схема алгоритма приведена на рис. 3. 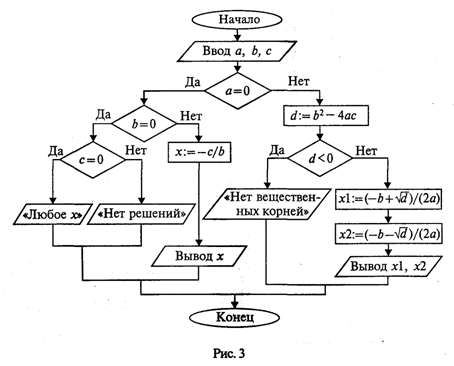 Этот же алгоритм на алгоритмическом языке:  В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий: 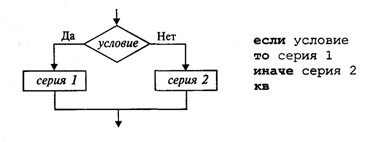 Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется серия 1 — последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется серия 2 (отрицательная ветвь). В АЯ условие записывается после служебного слова если, положительная ветвь — после слова то, отрицательная — после слова иначе. Буквы кв обозначают конец ветвления. Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «Корни квадратного уравнения». Рассмотрим следующую задачу: дано целое положительное число п. Требуется вычислить n! (n-факториал). Вспомним определение факториала: 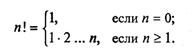 На рис. 4 приведена блок-схема алгоритма. В нем используются три переменные целого типа: n — аргумент; i — промежуточная переменная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n = 3. 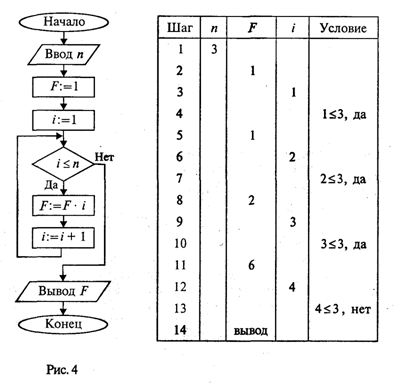 Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке. Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.  Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда цикл-пока, или цикл с предусловием. Общий вид команды цикл-пока в блок-схемах и в алгоритмическом языке следующий: 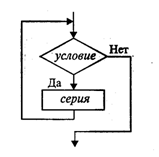 пока условие, повторять нц серия кц Выполнение серии команд (тела цикла) повторяется, пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слова нц и кц обозначают начало цикла и конец цикла соответственно. Цикл с предусловием — это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если а = 0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных, и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля — еще один признак хорошего качества программы. 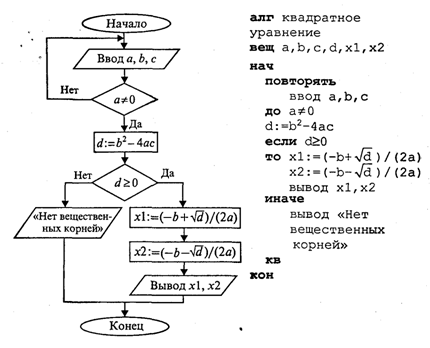 В общем виде структурная команда цикл с постусловием или цикл—до представляется так: 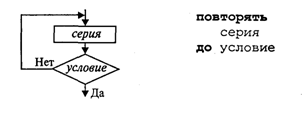 Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу. Составим алгоритм решения следующей задачи: даны два натуральных числа М и N. Требуется вычислить их наибольший общий делитель — НОД(М, N). Эта задача решается с помощью метода, известного под названием алгоритма Евклида Его идея основана на том свойстве, что если M > N, то НОД(М, N) = НОД(М — N,N). Попробуйте самостоятельно доказать это свойство. Другой факт, лежащий в основе алгоритма, тривиален — НОД(М, M) = М. Для «ручного» выполнения этот алгоритм можно описать в форме следующей инструкции:
Блок-схема и алгоритм на АЯ будут следующими: 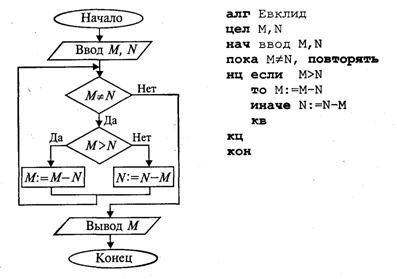 1.4. Вспомогательные алгоритмы и процедурыВ теории алгоритмов известно понятие вспомогательного алгоритма. Вспомогательным называется алгоритм решения некоторой подзадачи из основной решаемой задачи. В таком случае алгоритм решения исходной задачи называется основным алгоритмом. В качестве примера рассмотрим следующую задачу: требуется составить алгоритм вычисления степенной функции с целым показателем у = хk, где k — целое число, х ≠ 0. В алгебре такая функция определена следующим образом: 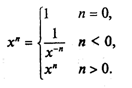 Для данной задачи в качестве подзадачи можно рассматривать возведение числа в целую положительную степень. Учитывая, что 1/х-n = (1/х) -n, запишем основной алгоритм решения этой задачи.  Здесь дважды присутствует команда обращения к вспомогательному алгоритму с именем СТЕПЕНЬ. Это алгоритм возведения вещественного основания в целую положительную степень путем его многократного перемножения. Величины, стоящие в скобках в команде обращения к вспомогательному алгоритму, называются фактическими параметрами. В учебном алгоритмическом языке вспомогательные алгоритмы оформляются в виде процедур. Запишем на алгоритмическом языке процедуру СТЕПЕНЬ.  Заголовок вспомогательного алгоритма начинается со слова «процедура», после которого следует имя процедуры и в скобках — список формальных параметров. В этом списке перечисляются переменные-аргументы и переменные-результаты с указанием их типов. Здесь а и k — формальные параметры-аргументы, z — параметр-результат. Следовательно, процедура степень производит вычисления по формуле z = аk. В основном алгоритме «Степенная функция» обращение к процедуре производится путем указания ее имени с последующим в скобках списком фактических параметров. Между формальными и фактическими параметрами процедуры должны выполняться следующие правила соответствия:
Фактические параметры-аргументы могут быть выражениями соответствующего типа. Обращение к процедуре инициирует следующие действия:
В процедуре степень нет команд ввода исходных данных и вывода результатов. Здесь присваивание начальных значений аргументам (а, п) производится через передачу параметров-аргументов. А присваивание результата переменной (у) происходит через передачу параметра-результата (z). Таким образом, передача значений параметров процедур — это третий способ присваивания (наряду с командой присваивания и командой ввода). Использование процедур позволяет строить сложные алгоритмы методом последовательной детализации. |
