Логика. Учебное пособие для студентов гуманитарных факультетов СанктПетербург 2001 оглавление
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
|
§ 3. ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ Между известными видами простых категорических суждений устанавливаются следующие отношения: противоречия (контрадикторности), противоположности (контрарности, противности), подпротивоположности (субконтрарности, подпротивности, или частичного совпадения) и подчинения. Отношение противоречия (контрадикторности) устанавливается между суждениями, разными как по качеству, так и по количеству, т.е. между общеутвердительным (А) и частноотрицательным (О) и между общеотрицательным (Е) и частноутвердительным (I). Отношение противоположности (контрарности, противности) устанавливается между общими суждениями, но разными по качеству: между общеутвердителным (А) и общеотрицательным (Е). Отношение подпротивоположности (подпротивности, субконтрарности, или частичного совпадения) устанавливается между разными по качеству частными суждениями, (между I и О). Наконец, в отношении подчинения находятся суждения одинакового качества, но разного количества, т.е. суждения общеутвердительное (А) и частноутвердительное (I), а также общеотрицательное (Е) и частноотрицательное (О). В этом отношении общее есть подчиняющее суждение, частное - подчиненное. Для наглядности и лучшего запоминания отношений между простыми категорическими суждениями в качестве мнемонической фигуры используют предложенный еще в средневековье так называемый логический квадрат. Углы этого квадрата соответствуют видам суждений, а стороны и диагонали - отношениям между ними: 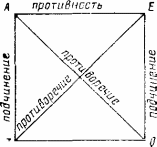 подпротивность Рассмотрим теперь самое главное - истинностные зависимости суждений, находящихся в этих отношениях. Отношение противоречия (контрадикторности) - самое четкое и определенное, можно сказать, жесткое отношение между суждениями. Противоречащие суждения не могут быть одновременно ни истинными, ни ложными. Это отношение соответствует принципу логики, выраженному законом исключенного третьего, согласно которому, если суждение А (общеутвердительное) истинно, то противоречащее ему суждение О (частноотрицательное) будет обязательно ложным, и наоборот. Таково же отношение и между частноутвердительным (I) суждением и общеотрицательным (Е). Отношение противоположности (противности, контрарности) неоднозначно. При истинности суждения А (или Е} ему противное суждение Е (или А) будет обязательно ложным. Но при исходной ложности суждения А (или Е), ему противное суждение Е (или А) может быть как истинным, так и ложным, что зависит только от конкретного содержания этих суждений. И снова, в конкретной ситуации лишь специалист в этой предметной области может окончательно решить, каким именно по истинностному своему значению будет противоположное исходному суждение. Например, исходное общеутвердительное (А) суждение «Все люди есть студенты» — ложно. По логике, противное ему суждение может быть как истинным, так и ложным. Зная предметную область, мы эту неопределенность снимаем и заключаем, что противное исходному общеотрицательное суждение (Е) «Ни один человек не является студентом» тоже ложно. Но вот другое по конкретному содержанию исходное суждение «Все люди имеют крылья». Оно тоже ложно, однако противное ему суждение «Ни один человек не имеет крыльев» — истинно. Особенность противоположных суждений кратко формулируется следующим образом: противоположные суждения не могут быть одновременно истинными, по крайней мере одно из них ложно, по большей мере - оба могут быть ложными. Отношение подпротивоположности (субконтрарности, частичного совпадения), можно сказать, обратно отношению противоположности, обратно по истинностным зависимостям. Это отношение устанавливается между разнокачественными частными суждениями, истинностные зависимости которых определяются нормой: подпротивоположные суждения не могут быть одновременно ложными, по крайней мере одно из них истинно, а по большей мере оба могут быть истинными. Так, при ложности исходного частноутвердительного суждения (I) ему подпротивное частноотрицательное суждение (О) будет обязательно истинным. То же самое и при ложности исходного частноотрицательного суждения — подпротивное ему суждение будет обязательно истинным. Например, суждение «Некоторые студенты имеют крылья» — ложно. Значит, подпротивное ему суждение должно быть обязательно истинным. И это так — «Некоторые студенты не имеют крыльев». Зато при истинности исходного частного суждения (I или О) ему подпротивное (О или I) может быть и истинным: "Некоторые студенты - спортсмены" и подпротивное ему "Некоторые студенты не есть спортсмены" оба истинны. Отношение подчинения характерно тем, что истинность общего (подчиняющего) суждения А (или Е) всегда влечет за собой истинность подчиненного ему частного суждения I (или О). Ложность же общих суждений не гарантирует ни истинности, ни ложности соответствующих им частных суждений, т.е. те могут быть в зависимости от конкретного содержания как истинными, так и ложными. Например, при истинности общего суждения «Все студенты - учащиеся», подчиняющееся ему частное суждение «Некоторые студенты - учащиеся» будет обязательно истинным. Ложность конкретного по содержанию общего суждения «Все студенты - отличники» позволяет конкретизировать истинностное значение подчиняющегося ему частного суждения «Некоторые студенты - отличники» — оно в данном случае истинно. В другом случае, при ложности общего суждения «Все студенты - птицы», подчиненное ему частное суждение тоже будет ложным: «Некоторые студенты - птицы». Ложность подчиняющихся частных суждений (I или О) всегда определяет ложность и соответствующих им общих суждений (А или Е). Истинность же частных — неопределенность общих: те могут быть в конкретных по содержанию случаях как истинными, так и ложными: «Некоторые студенты есть спортсмены» — истинное частное суждение. Общее же суждение «Все студенты есть спортсмены» будет ложным. Другой случай: истинное частное суждение «Некоторые студенты не есть птицы» и истинное же общее суждение «Все студенты не есть птицы». Зато ложность любого частного суждения («Некоторые студенты не есть учащиеся» или «Некоторые студенты есть птицы») всегда влечет ложность и соответствующего им общего суждения («Все студенты не есть учащиеся» или «Все студенты есть птицы»). Зная отношения между простыми категорическими суждениями (ориентируясь по логическому квадрату), легко составить сводную таблицу зависимости истинности того или иного суждения от истинности или ложности исходного. При истинности общеутвердительного суждения (А) общеотрицательное суждение (Е) будет ложно, частноотрицательное суждение (О) тоже будет ложно, частноутвердительное (I) — истинно. При ложности общеутвердительного суждения (А) общеотрицательное суждение (Е) будет неопределенным, частноотрицательное (О) будет истинным, частноутвердитсльное (I) — неопределенным. При истинности общеотрицательного суждения (Е) общеутвердительное (А) будет ложно, частноутвердительное (I) — тоже ложно, частноотрицательное (О) — истинно. При ложности общеотрицательного суждения (Е) общеутвердительное (А) — неопределенно, частноутвердительное (I) — истинно, частноотрицательное (О) — неопределенно. При истинности частноутвердительного суждения (I) общеутвердительное (А) — неопределенно, общеотрицательное (Е) — ложно, частноотрицательное (О) — неопределенно. При ложности частноутвердительного суждения (I) общеутвердительное суждение (А) ложно, общеотрицательное (Е) — истинно, частноотрицательное (О) — истинно. При истинности частноотрицательного суждения (О) общеутвердительное (А) — ложно, общеотрицательное (Е) — неопределенно, частноутвердительное (I) — тоже неопределенно. При ложности частноотрицательного суждения (О) общеутвердительное суждение {А) — истинно, общеотрицательное (Е} — ложно, а частноутвердительное (I) — истинно. Обозначив истинность буквой «и», а ложность — буквой «л», и используя символику для простых категорических суждений, суммируем эти зависимости в следующей таблице: А Е I О А Е I О § 4. ОПЕРАЦИИ С ПРОСТЫМИ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ Накопленное богатство знаний об этой форме мысли послужит нам базой для определенных действий, операций с суждением. Действия эти совершаются с суждением как целостным единством составных его элементов и не меняют исходную истинностную характеристику этого суждения; действия также не должны нарушать другие требования и законы логики. Операции - это, условно говоря, "практические" интеллектуальные действия с данной формой мысли, реализующие накопленные о ней знания. К логическим операциям с простыми категорическими суждениями относятся отрицание, обращение, превращение и противопоставление. Помимо этих операций к действию с суждениями следует отнести и преобразования по логическому квадрату, которые позволяют, исходя из одного суждения, получить три остальных с определенными истинностными характеристиками. Некоторые авторы рассматривают эти действия как "непосредственные" умозаключения, т.е. как выводы из одного исходного суждения (посылки); однако, данная операция не дает нового суждения, которое бы несло и новое содержание, что свойственно умозаключению, а выступает лишь действием по видоизменению элементов исходного суждения. Отрицание суждения связано, естественно, с отрицательной частицей "не" и прежде всего понимается как отрицание главного элемента этой мыслительной структуры - связки, как замена утвердительной на отрицательную и наоборот, т.е. отрицать можно не только утвердительное суждение, но и отрицательное. Такое понимание отрицания суждения можно считать главным. Этим действием истинное исходное суждение превращается в ложное, а ложное - в истинное. Однако, отрицать исходное суждение можно по-разному. Можно отрицать суждение через отрицание квантора, через отрицание субъекта, через отрицание предиката, через отрицание нескольких элементов суждения сразу. Не всегда подобные действия (в силу сложности структуры суждения) могут гарантировать сохранение истинности исходного суждения. В традиционном курсе логики отрицание суждения специально и обстоятельно не рассматривается. Здесь много сложностей, в частности: так как суждение "Не все S есть Р" тождественно частноутвердительному суждению "Некоторые S есть Р", то получается, что даже подчиненное суждение порой может выступать отрицанием общего: общеутвердительное суждение "Все S есть Р" можно отрицать частноутвердительным же суждением "Только некоторые S есть Р", или "Не верно, что все S есть Р". Боле разработанной в логике является операция отрицания суждения под названием превращение. Превращение представляет собой операцию, связанную с изменением качества исходного суждения (т.е. связки), при этом предикат выводного суждения должен противоречить предикату исходного. Таким образом, утвердительное суждение превращается в отрицательное, а отрицательное в утвердительное. Превращение есть операция с использованием в сущности двойного отрицания: первое отрицание — замена связки на противоположную, второе — замена предиката исходного суждения противоречащим ему понятием. По формуле это будет выглядеть: S есть Р или S не есть Р S не есть не-P S есть не-Р Общеутвердительное суждение превращается в общеотрицательное. В смысловом отношении оба эти суждения одинаковы, но логический вид их различен: Все студенты есть учащиеся (А) Все S есть Р Все студенты не есть не-учащиеся [Е). Все S не есть не-P Общеотрицательное суждение превращается и общеутвердительное: Все рыбы не есть млекопитающиеся (Е) Все S не есть Р Все рыбы есть не-млекопитающиеся (А) Все S есть не-P Частноутвердительное суждение превращается в частноотрицательное: Часть студентов есть спортсмены (I) Некоторые S есть Р Часть студентов не есть не-спортсмены (О). Некоторые S не есть не-Р Частноотрицательное суждение превращается в частноутвердительное: Некоторые книги не есть интересные (О) Некоторые S не есть Р Некоторые книги есть не-интересные (I). Некоторые S есть не-Р. Итоговая таблица: А превращается в Е Е превращается в А I превращается в О О превращается в I Обращение — логическая операция с простым категорическим суждением, заключающаяся в перестановке местами субъекта и предиката исходного суждения. Таким образом, субъект исходного суждения становится предикатом выводного суждения, а предикат исходного — субъектом выводного. При этом качество суждения и объем входящих в него понятий не меняются. Обращение — операция довольно простая, в символах выполняется почти механически. Если исходное суждение имеет вид «S есть Р», то выводное, получаемое в результате обращения, будет «Р есть S»: Такая обобщенная форма записи обращения не учитывает особенностей видов простого категорического суждения, а тем самым и объемных характеристик, входящих в суждение понятий. С учетом же их, общеутвердительное суждение (А) обращается, как правило, в частноутвердительное (I), ибо предикат в утвердительном суждении, как известно, нераспределен. А согласно требованию логики, соответственно закону тождества, понятие (иначе говоря — термин: этим словом в логике называют любое понятие, входящее в суждение), не распределенное в исходном суждении, не может быть распределено в выводном. В тех исключительных случаях, когда объемы предиката и субъекта общеутвердительного суждения тождественны между собой, обращение может быть прямым, без ограничения, т.е. общеутвердительное суждение обратимо в общеутвердительное: «Все квадраты есть ромбы с прямыми углами» обращается в общеутвердительное суждение «Все ромбы с прямыми углами есть квадраты». В большинстве же случаев общеутвердительное суждение обращается в частноутвердительное: «Все студенты — учащиеся» «Некоторые учащиеся — студенты». Общеотрицательное суждение (Е) в силу того, что в нем и субъект и предикат всегда распределены, будет обращаться прямо, без ограничения в общеотрицательное: Ни один круг не есть треугольник (Е) Ни один треугольник не есть круг (Е) Частноутвердительное суждение обращается в частноутвердительное же, что вполне понятно, ибо в этом суждении и субъект и предикат нераспределены. Такое обращение называется тоже прямым: Некоторые спортсмены — студенты (I) Некоторые студенты — спортсмены (I) Тот исключительный для частноутвердительного суждения случай, когда объем предиката его полностью входит в объем субъекта этого же суждения, т.е. когда предикат есть вид по отношению к субъекту (роду), и поэтому распределен, в этом случае частноутвердительное суждение обращается в общеутвердительное. Этом случай называется обращением с обобщением. Выполнить эту операцию можно, лишь зная истинность конкретного по содержанию суждения: Некоторые учащиеся - студенты (I) Все студенты - учащиеся (А) Что касается частноотрицательного суждения, то оно, как общепринято в логике, считается не поддающимся обращению. И это достаточно очевидно, ибо формула частноотрицательного суждения «Некоторые S не есть Р» не позволяет однозначно уточнить соотношение его субъекта и предиката. Между тем, оно допускает три случая, в круговых схемах выразимых так: Некоторые S не есть Р 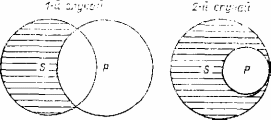 Какой именно вариант соотношения субъекта и предиката имеется в виду, из формулы частноотрицательного суждения не ясно. Снять эту неопределенность возможно лишь зная конкретное содержание исходного суждения, но логика конкретным содержанием не занимается, поэтому она отказывается от обращения такого суждения и это записано в большинстве учебников по логике. Однако, как нам представляется, частноотрицательное суждение можно обращать и во всех отмеченных случаях. Даже более того, для обращения частноотрицательного суждения не обязательно и знать конкретное содержание его: во всех случаях результатом обращения будет общеотрицательное суждение, т.е. возможно обращение с обобщением, хотя для первого случая более естественным является обращение прямое. Например: Некоторые студенты не есть спортсмены (О) Некоторые спортсмены не есть студенты (О). Но это же суждение может обращаться и в общеотрицательное. Обоснование таково: так как во всех отрицательных суждениях предикат всегда распределен, то он при перестановке его на место субъекта выводного суждения может браться во всем своем объеме: Некоторые студенты не есть спортсмены (О) Все спортсмены не есть эти "некоторые студенты"(Е} И во 2-м случае частноотрицательное суждение, опять же, обращается в общеотрицательное: Некоторые учащиеся не есть студенты (О) Все студенты не сеть эти «некоторые учащиеся» [Е) Так же и в 3-м случае обращение частноотрицательного суждения возможно с обобщением, например: Некоторые студенты не есть птицы (О) Все птицы не есть эти ''некоторые студенты" (Е) Хотя в этом последнем случае, как мы знаем из действительности, не только "некоторые студенты", но все они не есть птицы, однако, по принципиальным для логики соображениям, мы не меняем объем исходного понятия, так как термин, не распределенный в исходном суждении, не может быть распределенным в выводном. Итоговая таблица для операции обращения следующая: А обращается в I (А) Е обращается в Е I обращается в I (А) О не обращается Такова общепринятая таблица, но так как мы отстаиваем иную точку зрения, а именно, что частноотрицательное суждение тоже обращается, то добавляем: О обращается в Е. Последняя логическая операция — противопоставление — есть действие, в результате которого меняется качество исходного суждения (связка меняется на противную), меняются местами субъект и предикат его, и при этом субъект (или предикат) выводного суждения должен противоречить предикату (или субъекту) исходного. Эта операция может рассматриваться и как самостоятельная, и как комбинированная из двух предшествующих. Противопоставленное исходному суждение мы можем получить двумя способами. Первый способ: вначале исходное суждение (Все S есть Р) превращается (Все S не есть не-Р), а потом превращенное обращается (Все не-Р не есть S). В данном случае, конечное суждение будет противопоставленным предикату исходного суждения. Второй способ: вначале исходное суждение (Все S есть Р) обращается (Некоторые P есть S), а потом обращенное превращается (Некоторые Р не есть не-S). Здесь конечное суждение будет противопоставленным субъекту исходного суждения. Такой результат получить применяя операцию противопоставления сразу, руководствуясь ее определением, значительно сложнее, особенно в связи с получением из общего суждения частного. Например: Все S есть Р Некоторые Р не есть не-S. Поэтому, более простой и надежный вариант - поэтапное противопоставление, последовательное выполнение превращения и обращения в одном случае, и наоборот - в другом. Общеутвердительное суждение противопоставляется в общеотрицательное (противопоставление предикату), и в частноотрицательное (противопоставление субъекту). Например: Все студенты — учащиеся Все студенты — учащиеся Все не-учащиеся не есть студенты. Некоторые учащиеся не есть не-студенты. Общеотрицательное суждение противопоставляется в частноутвердительное (противопоставление предикату), и в общеутвердительное (противопоставление субъекту). Например: Все студенты не есть птицы Все студенты не есть птицы Некоторые не-птицы есть студенты. Все птицы есть не-студенты Частноутвердительное суждение не противопоставляется предикату, потому что уже первая процедура - превращение частноутвердительного исходного суждения - даст нам частноотрицательное, а оно, как известно, не обращается; противопоставление, тем самым, не завершается. Субъекту же частноутвердительное суждение противопоставляется. Выполним эту операцию поэтапно: Некоторые студенты - спортсмены Некоторые спортсмены - студенты Некоторые спортсмены не есть не-студенты Частноотрицательное суждение, наоборот, противопоставляется предикату частноутвердительным суждением, и не противопоставляется субъекту, поскольку чрстноотрицательное суждение не обращается. Например: Некоторые студенты не есть спортсмены Некоторые студенты есть не-спортсмены Некоторые не-спортсмены есть студенты Продолжая же реализовывать нашу особую точку зрения на обращение частноотрицательного суждения, следует отметить, что с этой точки зрения возможны как противопоставление частноутвердительного суждения предикату, так и противопоставление частноотрицательного суждения субъекту. При противопоставлении частноутвердительного суждения предикату получаем общеотрицательное суждение, а при противопоставлении частноотрицательного субъекту - общеутвердительное суждение. Например: Некоторые студенты - спортсмены Некоторые студенты не есть не-спортсмены Все не-спортсмены не есть эти "некоторые студенты" Некоторые студенты не есть спортсмены Все спортсмены не есть эти "некоторые студенты" Все спортсмены есть не эти "некоторые студенты" Сводная таблица операций с простыми категорическими суждениями |
