учебное пособие ТА. Учебное пособие по дисциплине Теория алгоритмов предназначено для студентов Политехнического колледжа НовГУ, обучающихся по специальности 230115 Программирование в компьютерных системах
 Скачать 0.51 Mb.
|
1.4 ЦИКЛЫ В ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМАХОпределение 4. Циклические алгоритмы – алгоритмы, содержащие фрагменты повторения вычислений. В зависимости от того, известно ли наперед число повторений некоторого участка алгоритма или нет, выделяют циклы арифметические и итерационные. В арифметических циклах число повторений вычислений известно и определяется счетчиком цикла. При каждом очередном вычислении значение счетчика изменяется на заданную величину и сравнивается с установленным количеством повторений. Если эти величины совпадают, то происходит выход из цикла по счетчику. В противном случае повторения вычислений продолжаются. Если перед началом цикла значение счетчика превышает заданное число повторений, то цикл не выполняется вообще. Возможен принудительный выход из цикла по некоторому наперед заданному значению. В итерационных циклах число повторений неизвестно, выход из цикла осуществляется при выполнении некоторого условия. В случае, когда условие проверяется до начала повторений, циклы называются с предусловием, когда же проверка происходит после очередной итерации, циклы называются с постусловием. Все арифметические циклы – это циклы с предусловием. [2] Общий вид блок-схем циклических алгоритмов представлен в таблице 2. Рассмотрим примеры решения задач с помощью циклических алгоритмов. В Приложении 1 представлены программы на языке Pascal, соответствующие данным задачам. Задача 4.
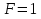  Начало 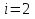 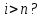 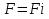 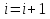   Нет Да Рис. 5 Алгоритм вычисления функции n! Задача 5.
Задача 6.
Задача 7.
Начало 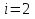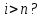Нет Да 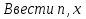 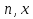 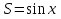 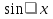 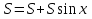 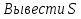 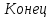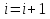Рис. 6 Алгоритм вычисления выражения 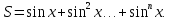 Вывести a, b, НОД, НОК Начало Ввести a, b 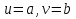 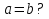 Да 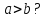 Нет Нет 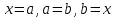 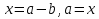 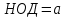 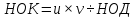 Конец Рис.7 Алгоритм Евклида нахождения НОД и НОК двух целых чисел Начало Конец m,n,k k K=0 K=k+1 m=m div 10 m<>0 Рис.8 Алгоритм подсчета количества цифр в натуральном числе. 4. Программа для решения задачи 7 (подсчет количества цифр в числе) представлена в Приложении 1, Program7.pas. |
.
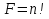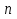натуральных чисел 1*2*3…n, 
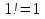. Вычисление значения факториала можно рассматривать как последовательное повторение операции умножения предшествующего значения факториала F на очередное натуральное число. 
схема алгоритма вычисления факториала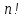 
на рис.5.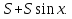
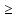b. Если b = 0, то НОД(a, b) =a, а если b 
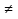0, то для чисел a,bиr, где r – остаток от деления aна b, выполняется равенство НОД (a, b) = НОД(b, r). Действительно, r:=a Mod b, r:= a –(a Divb) * b. Если какое-то число делит нацело и a, и b, то из приведенного равенства следует, что оно делит нацело и число r.