учебное пособие ТА. Учебное пособие по дисциплине Теория алгоритмов предназначено для студентов Политехнического колледжа НовГУ, обучающихся по специальности 230115 Программирование в компьютерных системах
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
1.2 ЛИНЕЙНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫОпределение 2. Линейный алгоритм – это алгоритм, содержащий алгоритмическую структуру «следование. Общий вид блок-схемы линейного алгоритма представлен в таблице 2. Рассмотрим 1-3 этапы решения задачи на ЭВМ с помощью линейного алгоритма.[2] Задача 2.
Блок-схема алгоритма представлена на рис.3. Начало Конец Ввести 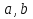 Вывести 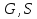 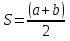 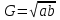 Рис. 3 Алгоритм вычисления среднего арифметического и среднего геометрического двух чисел. 1.3 ВЕТВЛЕНИЕ В ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМАХОпределение 3. Конструкция ветвления - это часть алгоритма, в которой в зависимости от выполнения или невыполнения некоторого условия выполняется либо одна, либо другая последовательность действий. Алгоритм, в котором используется конструкция ветвления, называется алгоритмом с ветвлением. Общий вид блок-схем алгоритма ветвления представлен в таблице 2. Для реализации алгоритмов с разветвленной структурой в языках программирования используются условные операторы. Рассмотрим пример решения задачи с помощью алгоритма ветвления. Задача 3.
Начало конец 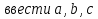 Вывести корни равные x Вывести корни дейст. x1,x2 Вывести корни комплекс. x1,x2 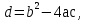  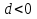 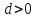 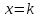 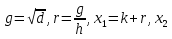 =k-r =k-r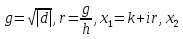 =k-ir =k-irнет нет да да Рис. 4 Алгоритм вычисления корней квадратного уравнения. |

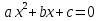 с действительными коэффициентами
с действительными коэффициентами 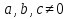 , когда
, когда 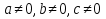 .
.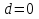 , и комплексные сопряженные корни, если
, и комплексные сопряженные корни, если 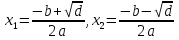 . Равные корни определяются так:
. Равные корни определяются так: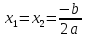 . Комплексные сопряженные корни вычисляются так же, как и действительные, только представляются двойкой чисел
. Комплексные сопряженные корни вычисляются так же, как и действительные, только представляются двойкой чисел 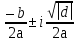 , где знак
, где знак 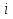 указывает на то, что
указывает на то, что 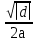 – мнимая часть значения корня. В алгоритме вычисления корней на первом этапе должно быть предусмотрено вычисление значения дискриминанта
– мнимая часть значения корня. В алгоритме вычисления корней на первом этапе должно быть предусмотрено вычисление значения дискриминанта 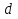 и дальнейшая проверка его знака.
и дальнейшая проверка его знака.