учебное пособие ТА. Учебное пособие по дисциплине Теория алгоритмов предназначено для студентов Политехнического колледжа НовГУ, обучающихся по специальности 230115 Программирование в компьютерных системах
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
1.5 МАШИНА ПОСТАВ 1936 году американский математик и логик Эмиль Леон Пост (1897–1954) предложил абстрактную вычислительную конструкцию, позволяющую формально определить алгоритм и названную впоследствии машиной Поста. При разработке вычислительной конструкции Пост руководствовался принципом создания максимально простой абстракции: минимумом операций при обработке информации, входная информация должна быть закодирована с использованием минимального набора символов. В теории алгоритмов существует так называемый “тезис Поста”: “Всякий алгоритм представим в форме машины Поста”. Этот тезис одновременно является формальным определением алгоритма. Алгоритм(по Посту) — программа для машины Поста, приводящая к решению поставленной задачи. Тезис Поста является гипотезой. Его невозможно строго доказать (так же, как и тезис Тьюринга), потому что в нем фигурируют, с одной стороны, интуитивное понятие “всякий алгоритм”, а с другой стороны — точное понятие “машина Поста”. Для того чтобы опровергнуть гипотезу Поста, необходимо придумать алгоритм, который невозможно записать в виде программы для машины Поста. На сегодняшний день такого алгоритма не существует. [12] Состав машины Поста. Машина Поста состоит из ленты и каретки. Лента бесконечна и разделена на секции одинакового размера — ячейки. 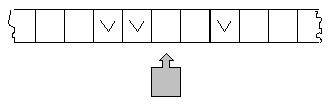 Рис. 9. Состав машины Поста В каждой ячейке ленты может стоять метка V либо ничего не записано.. Состояние ленты — это распределение меток по ячейкам. Состояние ленты меняется в процессе работы машины. Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной ячейки ленты, т.е. каретка обозревает одну ячейку. За единицу времени каретка может совершить одно из трех действий: стереть метку, поставить метку, совершить движение на соседнюю ячейку. Состояние машины Поста складывается из состояния ленты и положения каретки. Команды машины Поста: 1. записать 1 (метку), перейти к i-й строке программы; 2. записать 0 (стереть метку), перейти к i-й строке программы; 3. сдвиг влево, перейти к i-й строке программы; 4. сдвиг вправо, перейти к i-й строке программы; 5. останов; 6. если 0, то перейти к i, иначе перейти к j. Недопустимые действия, ведущих к аварийной остановке машины:
Команды машины обозначают следующим образом (рис.10):  Рис. 10 Команды машины Поста Рассмотрим несколько арифметических задач для машины Поста и их решение.[12] С помощью простейших операций, которыми располагает машина Поста, можно выполнять арифметические операции — основу любого современного процессора.
Решение: 1. ? 2; 3 (команды 1 и 2 — передвигаем каретку к массиву) 2. → 1 3. → 4 (команды 3 и 4 — передвигаем каретку к концу массива) 4. ? 5; 3 5. V 6 (команды 5–7 — ставим 2 метки в конце массива) 6. → 7 7. V 8 8. !
Решение. 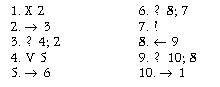 3. На ленте задана последовательность массивов, включающая в себя один и более массивов. При этом два соседних массива отделены друг от друга одной пустой ячейкой. Необходимо на ленте оставить один массив длиной равной сумме длин массивов, присутствовавших изначально. Каретка находится над крайней левой меткой первого (левого) массива. Решение. 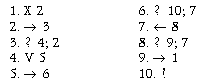 4. На ленте заданы два массива — m и n, m > n. Вычислить разность этих массивов. Каретка располагается над левой ячейкой правого массива. Решение: 1. → 2 (команды 1–3: ищем левую метку массива m) 2. ? 3; 1 3. ← 4 4. X 5 (стираем левую метку массива m) 5. ? 6; 7 6. → 5 7. X 8 (стираем левую метку массива n) 8. → 9 9. ? 12; 10 (стерли последнюю метку в массиве n?) 10. ←11 (ищем левый край массива m) 11. ? 10; 4 12. ! 5. На ленте задан массив. Удвоить массив в два раза. Каретка располагается над первой ячейкой массива. Решение. В результате работы программы справа от исходного массива будет сформирован новый массив удвоенной длины, исходный массив будет стерт.  |
