Учебное пособие по курсу Ядерная безопасность для студентов, обучающихся по направлению Ядерная энергетика и теплофизика
 Скачать 5.76 Mb. Скачать 5.76 Mb.
|
6.4 Закон ослабления узкого пучка. Слой половинного ослабленияРассмотрим ослабление в веществе нерассеянного излучения. Пусть на плоский слой вещества параллельно оси х падает пучок мононаправленных моноэнергетических частиц, с плотностью потока частиц при х=0 ф0. Выделим на глубине х слой dx. Изменение плотности потока нерассеянных частиц: 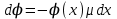 где- линейный коэффициент ослабления. После интегрирования получаем: 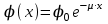 Данная формула представляет собой закон ослабления узкого пучка. Для коэффициента ослабления часто используют его представление в 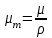 . .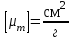 , в этом случае расстояние х измеряют в , в этом случае расстояние х измеряют в 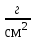 , , 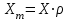 , , 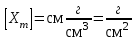 Слой половинного ослабления – это расстояние, на котором внутри данного материала плотность потока снижается вдвое. 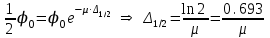 6.5 Поле излучения источников различной формыПользуясь выражением для закона ослабления узкого пучка, получим выражения для полей излучения источников различной формы. 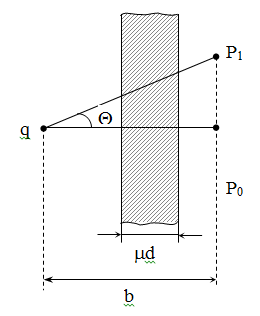 Точечный изотропный источник. Без защиты С защитой 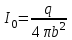 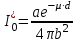 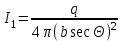 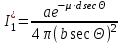 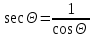 Рисунок 6.1 Линейный источник (трубопроводы, струя радиоактивных газов). Пусть ql – мощность на единицу длины. Вклад от участка dl в интенсивность излучения в точке P0  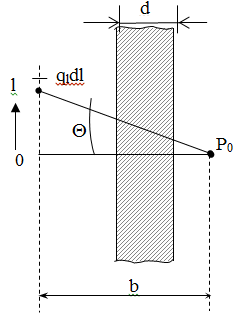 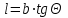 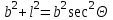 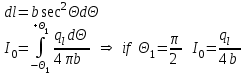 1 – предельное значение угла . В случае с защитой 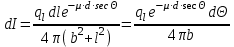 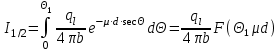 Рисунок 6.2 Рисунок 6.2Где 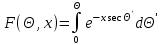 - интегральный секанс (функция Зиверта). - интегральный секанс (функция Зиверта).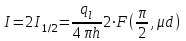 Плоский бесконечный источник (например, поверхность, на которую выпали радионуклиды). qs – мощность на единицу площади  d 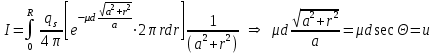   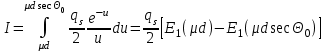 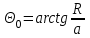 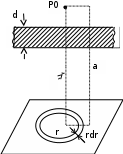 Если защиты нет (d = 0), тогда Если защиты нет (d = 0), тогда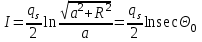 Для бесконечного плоского источника 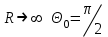 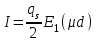 Рисунок 6.3. 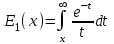 - специальная функция - специальная функция (интегральная показательная функция 1-го порядка). Источник в виде полубесконечного пространства (например, радиоактивное облако). qv – объемная плотность источника. 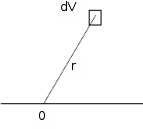 s – коэффициент ослабления в материале источника (т.е. в этом случае нужно учитывать самопоглощение в источнике). s – коэффициент ослабления в материале источника (т.е. в этом случае нужно учитывать самопоглощение в источнике).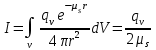 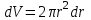  Рисунок 6.4. Для бесконечного пространства. 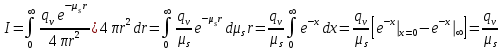 |
