Учебное пособие по курсу Ядерная безопасность для студентов, обучающихся по направлению Ядерная энергетика и теплофизика
 Скачать 5.76 Mb. Скачать 5.76 Mb.
|
Глава 8 Содержание Уравнение переноса излучения. Многогрупповое представление. Методы решения одногрупповых уравнений. Метод Монте-Карло. Вначале мы рассмотрели методы расчета доз от потоков гамма-квантов и нейтронов. Эти методы, развитые в первые десятилетия работы с ионизирующими излучениями, сегодня могут рассматриваться как инженерные и во многих задачах могут и сегодня успешно применяться. Альтернативой этим методам, особенно в нестандартных задачах, является прямое решение уравнения переноса частиц. Возможность использовать эту альтернативу существенно увеличилась благодаря развитию вычислительной техники и численных методов решения уравнения переноса. Ниже мы обсудим данное уравнение и некоторые методы его решения. 8.1 Уравнение переноса излученияДанное уравнение является интегро-дифференциальным уравнением и представляет собой линейный вариант более общего случая кинетического уравнения Больцмана переноса частиц, которое является нелинейным, так как учитывает взаимодействие частиц друг с другом. В нашем случае, учитывая, что плотность ионизирующих частиц (нейтронов, гамма-квантов или электронов) существенно меньше плотности атомов среды, в которой распространяется поток частиц, можно учитывать только взаимодействие частиц с атомами среды и не учитывать их взаимодействие между собой, что и делает уравнение переноса линейным. Напишем стационарный вариант уравнения переноса (в задачах защиты в основном достаточно стационарного варианта), а затем обсудим то, как оно получается. 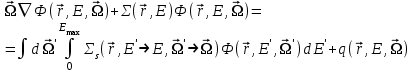 Уравнение описывает как перенос гамма-квантов, так и перенос нейтронов и электронов.  плотность потока частиц в точке плотность потока частиц в точке  с энергией Е, движущихся в направлении, задаваемым вектором с энергией Е, движущихся в направлении, задаваемым вектором  . Это иллюстрируется рисунком 8.1. . Это иллюстрируется рисунком 8.1.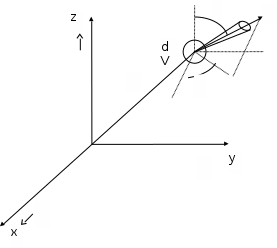 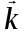 Рисунок 8.1 - Объяснение к уравнению переноса В объеме dV (шар) имеются частицы, движущиеся во всех направлениях. Мы выбираем некое направление 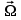 . В точке . В точке 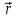 это направление задается полярным и азимутальным углами и . это направление задается полярным и азимутальным углами и .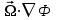 - утечка частиц из объема dV - утечка частиц из объема dV - оператор Набла (градиент) 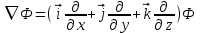 Ф – убыль частиц из элемента фазового пространства за счет рассеяния и поглощения. - сечение увода. 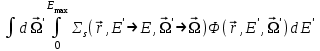 - поступление в рассматриваемый элемент объема за счет рассеяния при других энергиях и направлениях движения. - поступление в рассматриваемый элемент объема за счет рассеяния при других энергиях и направлениях движения.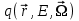 - источник частиц в данном элементе. - источник частиц в данном элементе.Уравнение переноса дополняется граничными условиями. Например: 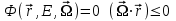 при при 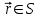 , где S – граничная поверхность рассматриваемой системы. , где S – граничная поверхность рассматриваемой системы.8.2 Многогрупповое представление уравнения переносаОсновной метод нахождения решения уравнения переноса – преобразование его в систему многогрупповых уравнений. Благодаря этому преобразованию удается исключить энергетическую переменную. Шкала энергий делится на интервалы – группы.  Уравнение переноса интегрируется по энергиям внутри каждой группы. Например, для группы с номером i от Еi-1 до Еi получаем: 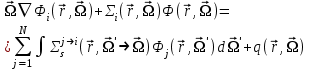 гдеi– номер энергетической группы, i = 1, 2, …. N; N – полное число групп; 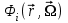 - групповая плотность потока частиц: - групповая плотность потока частиц: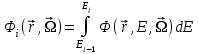 ; ;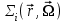 - групповое сечение увода частиц; - групповое сечение увода частиц; . .Так как 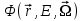 зависит от зависит от 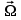 , то эта зависимость появляется и у , то эта зависимость появляется и у 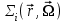 , хотя у , хотя у 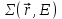 ее нет. ее нет.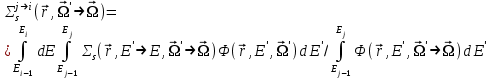 - сечение перевода частицы из группы j в группу i. - сечение перевода частицы из группы j в группу i.Наконец, 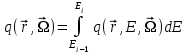 . .Получение групповых сечений представляет собой особую проблему. Видно, что в идеале для получения сечения 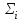 необходимо знать: необходимо знать:а). энергетическую зависимость 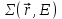 ; ;б). необходимо иметь вид функции 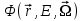 , т.е. уже иметь точное решение. , т.е. уже иметь точное решение.На практике используют некоторые предположения относительно энергетической зависимости Ф(Е) в пределах группы. Например, для замедляющихся нейтронов используют спектр Ферми 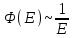 , для тепловых нейтронов – спектр Максвелла. , для тепловых нейтронов – спектр Максвелла.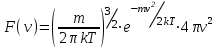 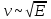 - скорость нейтрона. - скорость нейтрона.В пределах очень узких групп роль внутригруппового спектра снижается. Грубо говоря, для узкой группы подойдет и константа. Процедура решения системы многогрупповых уравнений сводится к решению одногрупповых (или иногда говорят односкоростных) уравнений. 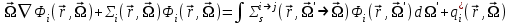 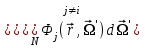 Т.е. в каждой группе вводится эффективный источник 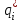 . В результате в каждой группе получаем одногрупповое уравнение, которое все еще является интегро-дифференциальным. . В результате в каждой группе получаем одногрупповое уравнение, которое все еще является интегро-дифференциальным. |
