Учебное пособие по курсу Ядерная безопасность для студентов, обучающихся по направлению Ядерная энергетика и теплофизика
 Скачать 5.76 Mb. Скачать 5.76 Mb.
|
8.3 Решение одногрупповых уравненийЧтобы продемонстрировать, как преобразуются полученные одногрупповые уравнения, далее рассмотрим это на примере одномерного приближения в плоской геометрии. Одномерный поток частиц движется вдоль оси z, испытывая рассеяние и поглощение на атомах среды. Для упрощения задачи будем считать, что рассеяние изотропно. Это значит, что можно записать: 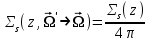  Т.е. после рассеяния частица может с равной вероятностью двигаться в любом направлении в пределах телесного угла 4. Т.е. после рассеяния частица может с равной вероятностью двигаться в любом направлении в пределах телесного угла 4.Член утечки  преобразуется следующим образом: преобразуется следующим образом: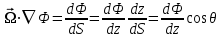 , , обозначим cos = , 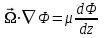 Получим уравнение:  Чтобы избавиться в этом уравнении от интеграла применяют следующий прием, называемый: 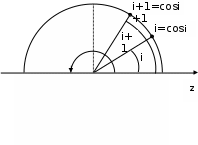 Метод дискретных направлений Метод дискретных направленийВыбирают дискретные направления, характеризующиеся углом θI или cosθi=μi. Интегро-дифференциальное уравнение (А) заменяют системой уравнений для плотности потоков (В)  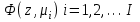 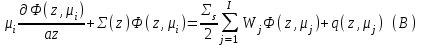 При этом 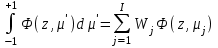 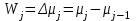 Получаем уже систему дифференциальных уравнений 1-го порядка. Далее для перехода от этой системы дифференциальных уравнений к системе алгебраических уравнений выполняется операция дискретизации по пространственной переменной. 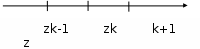 На оси z вводится система дискретных точек zk k = 1, 2, … K. Производная 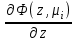 заменяется конечно-разностным выражением: заменяется конечно-разностным выражением: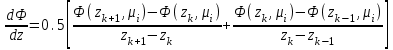 В результате каждое i-е дифференциальное уравнение системы (В) заменяется системой алгебраических уравнений вида: 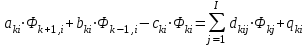 Система имеет размерность K x I, где K – число пространственных точек, I – число дискретных направлений. Если ввести вектор 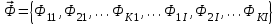 , ,эту систему можно записать в матрично-векторной форме: 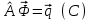 , ,где 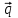 - вектор источников, - вектор источников, 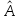 - матрица коэффициентов. - матрица коэффициентов.Для получения решения достаточно обратить матрицу 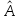 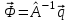 Реально это сделать сложно из-за большой размерности матрицы. Поэтому применяют следующий прием: 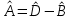 , где , где 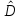 - диагональная матрица. - диагональная матрица.Уравнение (С) переписывают в виде 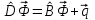 или 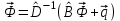 Эту систему решают итерационно: 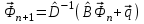 n = 0, 1, 2, …, где n – номер итерации. При n = 0 выбирают 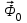 - начальное приближение вектора. Итерации считаются сошедшимися, и решение полученным, когда выполняется условие: - начальное приближение вектора. Итерации считаются сошедшимися, и решение полученным, когда выполняется условие: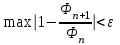 |
