Учебное пособие по курсу Ядерная безопасность для студентов, обучающихся по направлению Ядерная энергетика и теплофизика

• Название: Учебное пособие по курсу Ядерная безопасность для студентов, обучающихся по направлению Ядерная энергетика и теплофизика
• Дата: 22.04.2022
• Размер: 5.76 Mb.
• Имя файла: Total-3-6-new-bolshoy.docx
• Тип: Учебное пособие; #490571
• страница: 40 из 45

Вопросы по темам: Методы измерения доз. Особенности защиты на объектах ядерной техники. Аварии на объектах ядерной техники.

1.Ионизационные дозиметры (ионизационные камеры, конденсаторные камеры, счетчик Гейгера).

2. Полупроводниковые дозиметры.

3.Сцинтилляционные дозиметры.

4. Люминесцентные дозиметры.

5.Фотографический и химический методы дозиметрии.

6.Общие сведения о ядерном топливном цикле. Открытый и замкнутый циклы.

7.Радиационная опасность на урановых рудниках. Радиационная опасность на других предприятиях начальной стадии ЯТЦ. Регенерированный уран. Проблема урана –232.

8. Защита активной зоны ядерного реактора. Радиационное энерговыделение в защите.

9. Защита системы теплоносителя (составляющие активности теплоносителя, кислородная активность, роль кобальта, выход в теплоноситель продуктов деления).

10. Наиболее известные аварии на объектах атомной техники. Энергия Вигнера. Остаточное энерговыделение. Пароциркониевая реакция.

11. Международная шкала ядерных событий (INES).

12. Требования НРБ-99 по ограничению облучения населения в условиях радиационной аварии.

13. Проектные и запроектные аварии.

14 Барьеры на пути выхода активности.

15. Оценка радиационных последствий при аварии на АЭС (Накопление продуктов деления, выход под оболочку твэла, перенос активности по помещениям АЭС, распространение радиоактивного облака)

ЗАДАЧИ

Задачи к главам 1-2.

1. 
   Датирование археологических материалов.
   

Радиоуглерод ¹⁴С образуется из азота под действием космических нейтронов.

¹⁴N + n  ¹⁴C + p

¹⁴C распадается с периодом Т_1/2 = 5730 лет.

¹⁴С  ¹⁴N + β^- +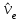

Так как живой организм постоянно обменивается с атмосферой СО₂, то устанавливается стабильное отношение ¹⁴С/¹²С = 1.3510^-12.

После гибели организма обмен прекращается, и отношение ¹⁴С/¹²С постоянно уменьшается из-за распада ¹⁴С. Измеренные активности углерода позволяют рассчитать момент гибели организма.
Пример: Предполагалось, что фрагмент кости, найденной в Мексике, принадлежал одному из солдат армии Кортеса, покорившей ацтеков в начале 16 века. Фрагмент содержит 200 г углерода и имеет активность 400 распад/мин = 6.7 Бк.

Скорость распада ¹⁴С в живом организме 15.6 распад/мин на 1 г углерода.

Тогда активность фрагмента кости в момент гибели:

200  15.6 = 3120 распад/мин.

Отношение активностей сегодня и в момент гибели: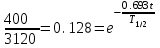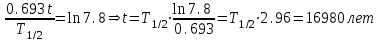





Отсюда следует, что первоначальное предположение неверно.

2. 
   Нейтронный активационный анализ.
   

После покупки золотой цепочки с 10% содержания золота недоверчивая покупательница облучила нейтронами звено цепочки весом 25 мг в потоке нейтронов 10¹⁰ н/см²с. После этого устройством с эффективностью 12% она измерила активность звена, которая оказалась равной 7.510⁴ Бк.
Сколько процентов золота по весу содержалось в цепочке?

1). При захвате нейтрона стабильным изотопом золота ¹⁹⁷Au образуется радиоактивный изотоп ¹⁹⁸Аu, который далее распадается.

¹⁹⁷Au + n  ¹⁹⁸Au  ¹⁹⁸Hg + β^- +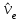
2). При облучении в потоке нейтронов концентрация ¹⁹⁸Au нарастает и через некоторое время устанавливается стационарное значение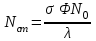



где σ = 98.8 барн – микроскопическое сечение захвата нейтронов ¹⁹⁷Au;

Ф – поток нейтронов;

N₀ – ядерная концентрация ¹⁹⁷Au в образце.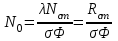



где - стационарная активность облученного образца.



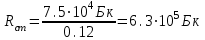(с учетом эффективности счетного устройства).

Масса золота в образце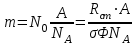



где А – масса г-моля золота 197г/моль;

N_А – число Авогадро 6.0210²³ ядер/моль;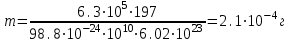



Процент золота в образце:

, т.е. примерно в 10 раз меньше заявленного.

3. 
   Рассчитать массу ²³⁸U с активностью 1 Кu. Т_1/2 = 4.510⁹ лет.
   

(Ответ 3 т).

Рассчитать массы ²³⁵U, ²³⁹Pu, ¹³⁷Cs, ¹³¹I, соответствующие активности

в 1 Ku.

4. 
   Первоначальная активность ⁶⁰Со равна 38 мКu. Т_1/2 = 5.27 года. Определить его активность через 3 года.
   

(Ответ 25.5 мКu).

5. 
   Сколько -частиц с кинетической энергией 4.9 МэВ, поглощенных в биологической ткани массой 1 г соответствует эквивалентной дозе 0.5 Зв?
   

(Ответ 0.3210⁸).

6. 
   Оценить поглощенную дозу -излучения в графите реактора РБМК за 30 лет эксплуатации. (Ответ 10¹¹ Гр).
   

7. 
   Месторождение урана в Западной Африке имеет содержание урана-235 0.64%, тогда как нормальное содержание урана-235 в уране – 0.72%.
   

Предполагают, что такое пониженное содержание в данном месторождении объясняется тем, что много лет назад в нем имела место самоподдерживающая реакция деления и часть урана-235 в ней “сгорела”.

Известно, что для возникновения самоподдерживающейся реакции в уран-водных системах обогащение должно быть на уровне 3%.

Какое количество лет назад такая ситуация могла иметь место?

Периоды полураспада урана-238 4.510⁹ лет, урана-235 0.710⁹ лет.

(Ответ 210⁹ лет).

8. 
   Чему равны интенсивность излучения и плотность потока -квантов для двух моноэнергетических пучков -излучения с энергиями фотонов 0.05 и 2 МэВ, если мощность экспозиционной дозы в каждом пучке равна 3 мР/с.
   

____________

Мощность экспозиционной дозы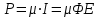



где  - коэффициент поглощения энергии в воздухе ( = 0.001293 г/см³)

 = 0.048610^-3 см^-1 (Е = 0.05 МэВ)

 = 0.036310^-3 см^-1 (Е = 2 МэВ)

Экспозиционная доза в 1 Р (2.0810⁹ пар ионов) соответствует энергии, поглощенной в воздухе в количестве:

0.114 эрг/см³ или 88 эрг/г

7.110⁴ МэВ/см³

Р = 310^-37.110⁴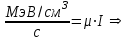

а) для Е = 0.05 МэВ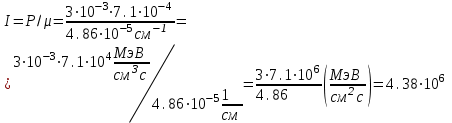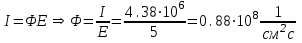


б) для Е = 2 МэВ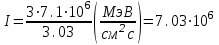

9. 
   Показать, что эквивалентами рентгена являются 2.0810⁹ пар ионов на 1 см³ воздуха, 7.110⁴ МэВ на 1 см³ воздуха, 0.114 эрг на 1 см³ воздуха, 1.6110¹² пар ионов на 1 г воздуха, 5.4610⁷ МэВ на 1 г воздуха и 88 эрг на 1 г воздуха.
   

10. 
    В 10 см³ воздуха при нормальных условиях под действием -излучения образовалось 8.310¹⁰ пар ионов. Чему равна керма в расчете на 1 г воздуха, если происходит равномерное облучение по бесконечно большому пространству?
    

(Ответ: 2.210⁸ МэВ/г)

11. 
    Чему равна поглощенная доза смешанного -нейтронного излучения в тканеэквивалентном по атомному составу материале, если экспозиционная доза -излучения равна 0.15 Р, а флюенс нейтронов = 310⁵ н/см²? Энергия -квантов равна 300 кэВ, а нейтронов 8 МэВ.
    

(Ответ: 130 мрад)

12. 
    Плотность потока -квантов меняется с течением времени по закону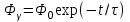
    

Найти величину кермы в воздухе за время облучения 2.4 час, начиная с t = 0, если  = 1.5 час, Ф₀ = 410⁹ 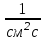и энергия -квантов 1 МэВ.

13. 
    Чему равна плотность тока частиц направленного моноэнергетического излучения с энергией 2.5 МэВ через площадку, нормаль к которой расположена под углом 30⁰ ч направлению распространения излучения, если плотность потока энергии излучения равна 1.2 Вт/м²?
    

(Ответ: 2.610⁸ ).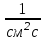

14. 
    Вблизи экватора за счет космического излучения на уровне моря образуется около 2.4 пар ионов на 1 см³ воздуха за 1 с, на высоте 6100 м – около 23 пар ионов на 1 см³ в 1 с. Чему равна экспозиционная доза за год, вызывающая такую ионизацию, если плотность воздуха на уровне моря 1.310^-3 г/см³, а на высоте 6100 м 1.110^-3 г/см³?
    

(Ответ: 36.5 мР; 414 мР).

15. 
    Экспериментатор находится в центральном реакторном зале в поле смешанного излучения. Мощность поглощенной дозы в биологической ткани, создаваемая быстрыми, тепловыми нейтронами и -излучением, равна 0.9, 1.3 и 2.1 мрад/сут соответственно. Определить мощность дозы в миллибэрах в неделю для шестидневной рабочей недели.
    

(Ответ: 90 мбэр/неделю).

16. 
    Число атомов в радиоактивном нуклиде с активностью 1.8 Ku равно 8.910¹³. Чему равен период полураспада нуклида?
    

(Ответ: 2.6 час).
Задачи к главам 6 -7

1. 
   1.Определить активность кобальта-60 (точечный источник), которая эквивалентна по создаваемой мощности экспозиционной дозы 1мКи радия. Гамма постоянная кобальта-60=12.9 Рсм**2./(час*мКи).
   

(Ответ: 0.65 мКи)

2. 
   Определить гамма-эквивалент, соответствующий активности натрия-24 равной 6мКи. Гамма постоянная натрия –24 равна 18.2 Р*см**2/(час*мКи).
   

(Ответ: 13мг Ra)

3. 
   Определить экспозиционную дозу, создаваемую точечным источником в 20 г экв. Ra за 30мин на расстоянии 1 м.
   

(Ответ: 8.4Р)

4. 
   Определить мощность экспозиционной дозы, создаваемую точечным источником на основе кобальта-60 активностью 900мКи на расстоянии 0.5м.
   

(Ответ: 4.64 Р/час)

5. 
   Гамма-эквивалент радиоактивного препарата кобальта-60 равен 0.5 г-экв Ra. Определить число распадов в препарате за 1 час.
   

6. 
   Определить -эквиваленты радиоактивных препаратов ²⁴Na, ⁶⁰Co, ¹³⁷Cs, ¹⁹²Ir активностью 10, 50, 100 и 250 мKu соответственно.
   

7. 
   В лаборатории имеется пять точечных -излучающих препаратов: ⁶⁰Co, ⁶⁵Zn, ^110mAg, ¹⁵⁵Eu активностью 10.6, 67.5, 9.8 и 103 мKu соответственно и 10.5 мKu радия в равновесии с дочерними продуктами распада. Какой источник следует использовать для эксперимента, чтобы получить максимальную мощность дозы при постоянной геометрии опыта?
   

(Ответ:⁶⁵Zn)

8. 
   На какое расстояние от точки детектирования следует удалить точечный изотропный источник ²⁴Na, активность которого к началу облучения составляла 300 мKu, чтобы за сутки облучения экспозиционная доза составила 50 Р? Ослаблением излучения в воздухе пренебречь.
   

(Ответ:r = 40.1 см)

9. 
   При определении -эквивалента точечного изотропного источника ²²⁶Ra в равновесии с основными дочерними продуктами распада измеренная мощность экспозиционной дозы -излучения точечным изотропным детектором, помещенным на расстоянии 1 м от источника оказалась равной 55 мкР/с. Определить -эквивалент источника. Ослаблением излучения в воздухе пренебречь.
   

(Ответ: 236 мг-экв Ra)

10. 
    В эксперименте используется точечный изотропный источник ¹³⁷Cs активностью 400 мKu, находящийся на расстоянии 1 м от точечного изотропного детектора. Определить мощность экспозиционной дозы в точке помещения детектора без защиты. Ослаблением излучения в воздухе пренебречь.
    

(Ответ: 34.4 мкР/с)

11. 
    Показать, что мощность экспозиционной дозы на оси линейного изотропного источника в произвольной точке вне его больше, а в любой точке на нормали к источнику, проходящей через его центр, меньше, чем мощность экспозиционной дозы от точечного изотропного источника с активностью, равной суммарной активности всего источника, и помещенного в центре линейного источника. Ослаблением излучения в воздухе и источнике пренебречь.
    

Решение.
Линейный источник будет выглядеть следующим образом.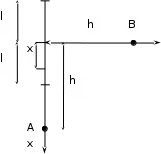

l – половина длины источника
h – расстояние от центральной точки источника до точки детектирования (А или В)

Точка А лежит на оси источника. Выражение для мощности дозы на оси источника (в точке А) получим по принципу суперпозиции.

Рассмотрим участок источника длиной dx в точке х.

Мощность дозы в точке А от источника dx дается выражением: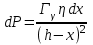



где Г_ - гамма-постоянная источника;

 - линейная удельная плотность активности.

Полная мощность дозы от всего линейного источника определяется интегрированием по длине источника от –l до +l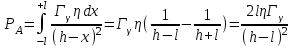


Величина Q = 2l равна полной активности источника.

Если теперь взять точечный источник с активностью Q, то для него выражение для мощности дозы: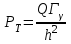

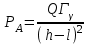, что всегда меньше, чем , что и требовалось показать.
Выражение для мощности дозы в перпендикулярном к источнику направлении (точка В) дается выражением: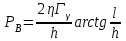

.

Это выражение также получается интегрированием по принципу суперпозиции.

Или .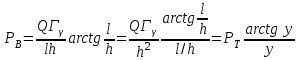

Т.е. мощность дозы в точке В равна мощности дозы Р_Т от точечного источника активностью Q, умноженному на arctgy/y, где y = l/h.
1). При h  0 y , arctg y /2.

Отсюда следует, что при малых hP_B< P_T.
2).При hy 0 в выражении 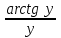получаем неопределенность типа 0/0.

По правилу Лопиталя предел этого выражения при h (y 0) равен .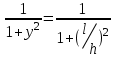

Отсюда следует, что при больших h также будет выполняться соотношение P_B< P_T, что и требовалось показать.

12. 
    Показать, что мощность экспозиционной дозы -излучения на расстоянии h от бесконечного линейного источника с равномерно распределенной активностью такая же, как в центре источника в виде полуокружности радиусом h с такой же линейной удельной активностью. Ослабление излучения в воздухе не учитывать.
    

13. 
    Линейный источник моделируется точечным изотропным источником, совершающим равномерное возвратно-поступательное движение от точки А до точки В. Определить необходимую активность точечного изотропного источника ¹³⁷Cs для получения в точке на расстоянии 0.5 м от середины линейного источника по перпендикуляру к нему экспозиционной дозы 1.5 мР за одно перемещение источника от А до В. Длина моделируемого источника 2 м. Источник перемещается со скоростью 20 см/с. Ослабление излучения в воздухе не учитывать.
    

(Ответ: 785 мKu)
Решение
За один проход от точки А до В набирается доза 1.5 мР. Отсюда следует, что средняя мощность дозы при движении источника от А до В равна 1.5 мР/t = 0.15 мР/с = 0.54 Р/час, так как время прохода t двухметрового участка при скорости движения 20 см/с равно 10 с.

Аналитическое выражение для мощности дозы Р конечного линейного источника имеется в справочниках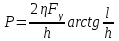

(1)

 – линейная удельная активность источника мКu/см – искомая величина;

F_– гамма-постоянная источника, которую берем из таблицы 1 Приложения для ¹³⁷Cs – 3.1 ;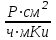

h – расстояние от источника до точки детектирования (в нашем случае 0.5 м);

l – половина длины линейного источника (в нашем случае 1 м).

Из выражения (1) находим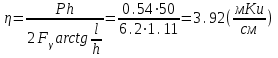



Учитывая, что длина источника 200 см = 2l получаем: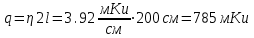

14. 
    Излучающее кольцо моделируется точечным изотропным источником ⁶⁵Zn активностью 100 мKu, движущимся равномерно со скоростью 10 см/с по окружности радиусом 50 см. Определить экспозиционную дозу после пяти оборотов в точке на расстоянии 1 м от центра окружности, считая по перпендикуляру к плоскости круга. Ослабление излучения в воздухе не учитывать.
    

(Ответ: 1.06 мР)
Решение
Мощность дозы кольцевого источника дается выражением, имеющимся в справочниках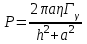



где  – линейная удельная активность (мКu/см);

Г_ – гамма-постоянная источника, которую берем из таблицы 1 Приложения для ⁶⁵Zn – 3.02 ;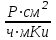

а – радиус кольца (в нашем случае 50 см);

h – расстояние от центра кольца до точки детектирования (в нашем случае 1 м).

Линейная удельная активность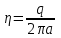



где q – заданная активность точечного источника 100 мКu.

Тогда .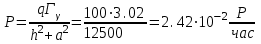

В соответствии с заданной скоростью движения источника 10 см/с один оборот займет t = 31.4 с.

Тогда доза, набегающая за 5 оборотов, определяется выражением: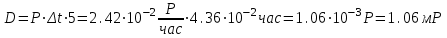

15. 
    После 7 час работы фильтра радиусом 0.5 м в потоке воздуха, загрязненного радиоактивными веществами, мощность экспозиционной дозы на расстоянии 1 м от центра фильтра, считая по перпендикуляру к его плоскости оказалась равной 2500 мкР/с. Определить загрязнение 1 см² фильтра в течение 1 часа, за время работы, если считать загрязнение равномерным по времени и поверхности фильтра. Распадом радиоактивного вещества, осевшего на фильтре и ослаблением излучения в фильтре и воздухе пренебречь.
    

(Ответ: 0.217 мг-экв Ra/(см²ч)
Решение
В данном случае источник излучения имеет форму диска. Выражение для мощности дозы от такого источника имеется в справочниках: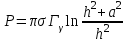

(3)

где  - поверхностная удельная активность (мКu/см²);

Г_ - гамма-постоянная источника ;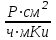

а – радиус диска (в нашем случае 0.5 м).
В этой задаче радиационный состав загрязнений фильтра неизвестен, следовательно неизвестны и Г_ - гамма-постоянные, определяющие мощность источника. Поэтому величину загрязнений фильтра будем выражать в терминах радиевого гамма-эквивалента.

Для этого используем соотношение 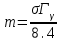следующее из определения радиевого гамма эквивалента, где m в нашем случае будет иметь размерность .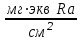

Величину m найдем, используя формулу (3)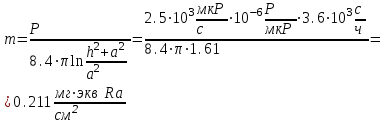



При условии равномерного по времени загрязнения его скорость будет равна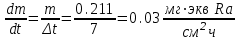

16. 
    В бассейне выдержки отработавшего топлива тепловыделяющие сборки хранятся под слоем воды глубиной 10 м. Используя универсальные таблицы для расчета защиты от -излучения оцените насколько возрастет мощность дозы излучения над поверхностью бассейна при уходе воды?
    

(Ответ: более 10⁷ раз)

17. 
    Во сколько раз снижает мощность дозы -излучения защита из бетона толщиной 1.5 м?
    

(Ответ: 10⁷ раз)

18. 
    Какую толщину защиты из железа требуется взять для снижения мощности дозы -излучения с энергией -квантов 1 МэВ на три порядка?
    

(Ответ: 20.5 см)

19. 
    Какая толщина защиты в предыдущей задаче получится в приближении узкого пучка?
    

(Ответ: 14.7 см)