Медков В.М. Демография, учебное пособие. Учебное пособие. Серия Учебники и учебные пособия
 Скачать 2.69 Mb. Скачать 2.69 Mb.
|
5.4. ПРОБЛЕМА УЧЕТА В АНАЛИЗЕ РОЖДАЕМОСТИ, ВКЛАДА ЕЕ ПОВЕДЕНЧЕСКИХ И СТРУКТУРНЫХ КОМПОНЕНТОВПонятие репродуктивного поведенияУровень рождаемости, складывающийся на той или иной территории (стране, регионе, континенте, земном шаре) в тот или иной период времени и измеряемый хорошо известными в демографии показателями (общий и суммарный коэффициенты рождаемости, специальный коэффициент рождаемости и др.), является функцией двух переменных. Одна из них - это демографическая структура, т. е. распределение населения по полу, возрасту, брачному и семейному состоянию. Другая переменная - это репродуктивное поведение, выражением которого в демографии являются среднее число детей в семье и среднее число детей, рожденное женщиной за всю ее жизнь. Под репродуктивным поведением понимается система действий и отношений, опосредующих рождение определенного числа детей в семье (а также вне брака)20. Два подходаВ демографии принято различать два основных подхода к измерению влияния репродуктивного поведения на уровень рождаемости, или, как еще принято говорить, степени намеренного ее ограничения. Эти подходы могут быть названы нормативным и эмпирическим. Последний также известен под названием «анализ промежуточных (непосредственных) переменных (детерминант) рождаемости». Нормативный подход ведет свое происхождение от методов стандартизации демографических коэффициентов, имеющих целью очистить их значения от влияния изменений возрастной структуры или повозрастной интенсивности демографических процессов. Суть методов стандартизации заключается в перевзвешивании повозрастных показателей, например, рождаемости (но также и смертности, брачности и так далее) по некоторой возрастной структуре, принимаемой за стандарт (прямая стандартизация), или, наоборот, возрастной структуры по значениям повозрастных демографических коэффициентов (косвенная стандартизация). Нормативный подход связан с представлениями о существовании некоего стандарта повозрастной брачной рождаемости, не ограничиваемой никаким вмешательством в репродуктивный цикл. Эта ничем не ограничиваемая «спонтанная» рождаемость получила название естественной рождаемости21. Как уже говорилось, понятие естественной рождаемости введено французским демографом Л. Анри22. Репродуктивное поведение в современных населениях не является естественным в указанном смысле. Оно включает в себя огромный объем прямого, специального, намеренного вмешательства в репродуктивный цикл («намеренного ограничения»). Это обстоятельство играет решающую роль в детерминации современного уровня рождаемости, который резко отличается от своего социально-биологического потенциала, выражающегося в понятии естественной рождаемости. Этот разрыв реальной и естественной рождаемости и характеризует, с точки зрения нормативного подхода, роль «намеренного ограничения», или, говоря социологически, роль репродуктивного поведения. Сопоставив фактическую рождаемость со стандартом естественной рождаемости, можно оценить соотносительную роль репродуктивного поведения и демографической структуры. В этом сопоставлении и заключается существо нормативного подхода. Эмпирический подход, в противоположность этому, не предполагает априорно существования какого-либо заранее данного стандарта естественной рождаемости (хотя это понятие употребляется и в рамках эмпирического подхода). Он как бы идет с другой стороны: исходя из реальной, фиксируемой статистикой или специальными социологическими исследованиями рождаемости, он как бы реконструирует, восстанавливает естественную рождаемость, или, говоря точнее, плодовитость. 5.4.1. Нормативный подходРазработка нормативного подхода связана с именами французского демографа Л. Анри, американских демографов Э. Коула и Дж. Трассела, российского демографа В.А. Борисова. Их объединяет общее для нормативного подхода представление о существовании стандарта естественной рождаемости, с которым сопоставляется рождаемость фактическая. Однако между позициями, с одной стороны, Л. Анри, Э. Коула и Дж. Трассела и, с другой, В.А. Борисова существует принципиальное различие. Если первые исходят из представлений о максимуме естественной рождаемости, определяемом к тому же в абсолютном смысле, т. е. вне зависимости от наличных социально-экономических условий, то В.А. Борисов выдвинул идею не максимума, а минимума естественной рождаемости, который имеет исторически-конкретный характер, обусловлен наличными социально-экономическими и санитарно-гигиеническими условиями, которые до и помимо всякого «намеренного вмешательства» ограничивают естественную рождаемость. Стремление определить максимум рождаемости ведет свою родословную от основоположника демографии Дж. Граунта. Еще в 1682 г. он пытался определить максимально возможный, говоря современным языком, общий коэффициент рождаемости. Граунт полагал, что на каждую 1000 жителей приходится 300 женщин в возрасте 15-49 лет, способных родить ребенка один раз в два года. Это дает величину общего коэффициента рождаемости, равную 150%о. В XIX в. И. Ваппеус высказал мнение, что теоретически возможный максимум общего коэффициента рождаемости равен 100%о, однако, по его мнению, этот максимум недостижим. Л. Анри считал, что в качестве максимума рождаемости следует брать реальную рождаемость, существовавшую на рубеже 1950-1960 гг. в населениях, отличавшихся особо высоким ее уровнем, - это прежде всего рождаемость в некоторых африканских странах. И использовать показатели повозрастной рождаемости этих населений в качестве стандарта естественной рождаемости. Э. Коул полагал, что брать в качестве стандарта естественной рождаемости показатели африканских стран было бы ошибкой, поскольку в этих странах низок уровень социально-экономического развития и санитарно-гигиенической культуры населения. В силу этого в африканских странах высоки показатели внутриутробной и младенческой смертности, которые искажают реальные показатели повозрастной рождаемости. По мнению Э. Коула, за стандарт следует принимать реальную рождаемость населений, в которых бы сочетались высокий уровень социально-экономического развития, высокая санитарно-гигиеническая культура, поголовная брачность, полное отсутствие какого-либо намеренного вмешательства в репродуктивный цикл, относительно короткий период грудного вскармливания, а также низкие уровни внутриутробной и младенческой смертности. Именно поэтому Э. Коул и предложил использовать в качестве стандарта естественной рождаемости показатели повозрастной рождаемости религиозной секты гуттеритов (браки, заключенные в 1920-х гг.). У гуттеритов уникально сочетаются хорошие санитарные условия, высокий уровень жизни, низкая смертность и неограничиваемая рождаемость. В течение длительного времени уровень рождаемости гуттеритов был самым высоким в мире и служил моделью максимальной рождаемости. Индексы рождаемости Э. КоулаЗадача определения стандарта естественной рождаемости встала перед Э. Коулом в связи с реализацией в конце 1960-х гг. проекта исследования снижения рождаемости в Европе в XVIII-XX вв., известного под названием «Принстонское исследование европейской рождаемости»23. Э. Коул в то время был директором Центра демографических исследований Принстонского университета. В распоряжении исследователей были только данные переписей европейских стран о распределении населения по полу и возрасту и о ежегодных числах родившихся. Информация о рождениях извлекалась, главным образом, из приходских записей о регистрации крещений. Такого рода данные позволяли рассчитывать только специальные коэффициенты рождаемости, но не ее суммарные коэффициенты, поскольку данные о распределении родившихся по возрасту матери отсутствовали. Но специальные коэффициенты рождаемости, как мы помним, не полностью свободны от влияния возрастной структуры. Пытаясь разрешить эту проблему. Э. Коул разработал три индекса рождаемости, известные ныне как индексы Коула24:
Эти индексы измеряли реальную рождаемость в ее соотношении со стандартом естественной рождаемости. По своей природе эти индексы являются примером косвенной стандартизации показателей рождаемости. Они выражают тот уровень рождаемости (ее общего коэффициента), который бы наблюдался в реальном населении, если бы повозрастные ее показатели были бы такими, как в стандарте естественной рождаемости, в качестве какового, согласно Э. Коулу, следует брать рождаемость гуттеритов, репродуктивное поведение которых соответствует перечисленным выше критериям. Наивысшие показатели брачной рождаемости гуттеритов были зафиксированы в 1920- 1930 гг. (табл. 5.5). Кроме того, им был предложен четвертый индекс - индекс брачной структуры (1т), который измеряет влияние на уровень рождаемости изменений брачной структуры населения. Индекс общей рождаемости (If) равен отношению наблюдаемого числа рождений к ожидаемому при условии, что реальное население имеет те же повозрастные показатели, что и стандарт естественной рождаемости: Таблица 5.5 Стандартные коэффициенты рождаемости, %о
Здесь В - годовое число рождений; ASFRX- наблюдаемые повозрастные коэффициенты рождаемости; Fx- среднегодовая численность женщин возраста x;ASFRs- повозрастные коэффициенты рождаемости стандарта (гуттеритов). Индекс брачной рождаемости (Ig) равен отношению наблюдаемого числа рождений в браке к ожидаемому при условии, что реальное население имеет те же повозрастные показатели брачной рождаемости, что и стандарт естественной рождаемости: 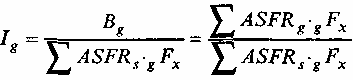 где Bg- годовое наблюдаемое число брачных рождений (Bg = ASFRggFx); ASFRg- наблюдаемые повозрастные коэффициенты брачной рождаемости; gFx- численность женщин возраста х, состоящих в браке; ASFRS- повозрастные коэффициенты рождаемости стандарта (гуттеритов). Индекс внебрачной рождаемости (Ih) равен отношению наблюдаемого числа рождений вне брака к ожидаемому при условии, что реальное население имеет повозрастные показатели внебрачной рождаемости, равные стандарту естественной рождаемости: 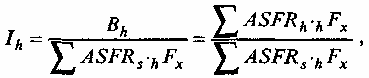 где Bh- годовое наблюдаемое число внебрачных рождений (Bh= ASFRh-hFx); ASFRh- наблюдаемые повозрастные коэффициенты внебрачной рождаемости; hFx- численность женщин возраста х, не состоящих в браке; ASFRs- повозрастные коэффициенты рождаемости стандарта (гуттеритов1 Индекс брачной структуры равен отношению ожидаемого числа брачных рождений к ожидаемому числу всех рождений: 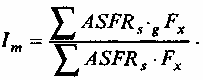 Это выражение можно представить иначе где gx - доля женщин возрастах, состоящих в браке, равная gFx/Fx Иначе говоря, индекс брачной структуры равен средневзвешенной доле женщин репродуктивного возраста, состоящих в браке, причем весами выступают повозрастные коэффициенты стандарта естественной рождаемости. Это позволяет легко рассчитывать индексIm, зная лишь повозрастные доли замужних женщин. Если же внебрачная рождаемость отсутствует, т. е. Ih = 0, то это соотношение равно: Поскольку Б = Bg + Bh и Fx = gFx + hFx, индексы рождаемости связаны между собой следующим соотношением: В табл. 5.6 приведен пример расчета индексов Коула для населения России (1994 г.). Как видно из таблицы, население России использует максимальный потенциал рождаемости менее, чем на 10%. Гипотетический минимум естественной рождаемости Российский демограф В.А. Борисов, разрабатывая свой вариант нормативного подхода, исходил из того, что использовать рождаемость гуттеритов в качестве стандарта естественной рождаемости методологически неправильно из-за уникальности этого субнаселения. По его мнению, таким стандартом может быть только стандарт, разработанный на основе математической модели репродуктивного процесса, так как только в этом случае можно «использовать массовые фактические данные». По мнению В.А. Борисова, более правильно определять не максимум, а минимум естественной рождаемости, чтобы быть уверенным, что уровень естественной брачной рождаемости не опустится ниже этого минимума в нормальных санитарных условиях. Поэтому в упомянутой математической модели надо брать такие значения ее параметров, которые находились бы в пределах санитарной нормы и были бы в ее пределах наименее благоприятными. Таблица 5.6 Иллюстративный пример расчета индексов Коула для населения России, 1994 г.
Исходя из этих предпосылок, В.А. Борисов производит расчет показателя брачной рождаемости для возраста 20- 24 года. В результате он получил значение повозрастного коэффициента рождаемости для этого возраста, равное 400%о. Для более старших возрастов он отступил от моделирования репродуктивного процесса, применив, подобно Л. Анри, усреднение показателей повозрастной рождаемости для 8 реальных населений, у которых величина ASFR2024 достоверно превышает 400%о, нормализацию ASFRдля более старших возрастов относительно возраста 20-24 года, а также преобразование модельного значения ASFR2024 в повозрастные показатели рождаемости с помощью этих коэффициентов нормализации25. В результате этой многоступенчатой процедуры В.А. Борисов получил свой стандарт естественной рождаемости, названный им «гипотетическим минимумом естественной рождаемости», или ГМЕР (табл. 5.7). По мнению В.А. Борисова, повозрастная рождаемость не может быть ниже этих значений, если отсутствуют какие-либо экстремальные обстоятельства. Относительно внебрачной рождаемости и в возрастах моложе 20 лет и старше 49 лет, В.А. Борисов полагал, что «наиболее верным представляется оставить фактическое число неизменным (т. е. считать, что число родившихся вне брака и у матерей моложе 20 лет и старше 49 лет в условиях естественной рождаемости было бы таким же, каким оно и есть фактически)»26. Затем, используя показатели повозрастной рождаемости стандарта и фактические данные о возрастной структуре женщин репродуктивного возраста, рассчитываются ожидаемые значения абсолютного числа рождений и общего коэффициента рождаемости, которые сопоставляются с фактическими. Разница между ожидаемыми и фактическими значениями характеризует степень реализации ГМЕР, масштабы распространенности среди населения намеренного ограничения рождаемости, роль поведенческой компоненты рождаемости и вклад репродуктивного поведения в ее уровень27. Таблица 5.7 Общие коэффициенты рождаемости (ОКР), гипотетический минимум естественной рождаемости (ГМЕР) и степень реализации ГМЕР в России28
Коэффициент ГМЕР одним числом характеризует брачно-возрастную структуру населения с точки зрения социально-биологического потенциала рождаемости. Увеличение или уменьшение величины коэффициента ГМЕР свидетельствует соответственно об улучшении или ухудшении брачно-возрастной структуры населения. Отношение же фактического общего коэффициента рождаемости к коэффициенту ГМЕР того же населения (а лучше, точнее: отношение фактического числа родившихся к гипотетическому) позволяет получить приближенное, но достаточно близкое к реальности представление о степени реализации потенциала рождаемости. Борисов В.А., Синельников А.Б, Брачность и рождаемость в России: демографический анализ. М., 1995. С. 80-81. На графике 5.2 приведены кривые, характеризующие повозрастную рождаемость гуттеритов, стандарт ГМЕР В.А. Борисова и фактическую рождаемость населения России в 1998 г. Используя коэффициенты ГМЕР, можно с помощью специальных График 5.2 Стандарты естественной рождаемости и фактическая повозрастная рождаемость населения России в 1998 году 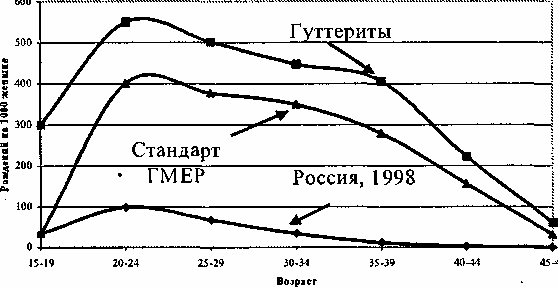 индексов* количественно оценить вклад в изменения рождаемости как поведенческих (степень реализации ГМЕР, т. е. распространенность внутрисемейного ограничения рождаемости), так и структурных (возрастного и брачного состава) компонентов (табл. 5.8). Данные таблицы ярко характеризуют решающую роль репродуктивного поведения в динамике общего коэффициента рождаемости в России во второй половине XX в. Обращает на себя внимание наличие двух периодов, когда роль внутрисемейного ограничения числа детей была особенно сильной, - 1958-1970 и 1989-1994 гг. В обоих случаях резкое падение рождаемости, имевшее место в эти годы, практически полностью объясняется именно действием фактора репродуктивного поведения - массовым переходом к модели соответственно двухдетной и однодетной семьи. Таблица 5.8 Факторная структура изменений общего коэффициента рождаемости в России в период между переписями населения (1959-1994, в % к его величине на начало каждого периода)29
Эти данные также свидетельствуют о том, что некоторый подъем рождаемости, происходивший в первой половине 80-х гг., был на самом деле статистическим артефактом: роль репродуктивного поведения в динамике общего коэффициента рождаемости по-прежнему была негативной. Переход к модели однодетной семьи продолжался. Правда, в те годы и власти, и некоторые демографы предпочитали не замечать этого, радуясь «неплохому», как выразился один из тогдашних руководителей КПСС и правительства СССР, «социально-демографическому эффекту» мер материальной поддержки семей, введенных в жизнь в начале 80-х годов. Впрочем, и в 60-е гг. власти и многие специалисты предпочитали не обращать внимания на падение рождаемости, полагая или делая вид, что оно является временным явлением, отражающим трудности развития нашей страны в первые послевоенные годы. Методологически подобное отношение к тогдашней динамике рождаемости можно объяснить приверженностью к концепции так называемой «прямой связи» между уровнем жизни и рождаемостью, незнанием или непониманием подлинных механизмов детерминации рождаемости и репродуктивного поведения, отсутствием внимания и интереса к социологическим проблемам демографических изменений. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
