Тесты по экономике 1 курс мед. Учебное пособие Специальность Педиатрия, Стоматология
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Тема «Инвестиции. Сложный процент и дисконтирование» Пример решения ситуационной задачи: Задача№1 Условие задачи: Рассчитайте будущую стоимость сегодняшних инвестиций в сумме 9 000 долларов, которая будет получена через два года при 9% годовых. Решение: Для решения задачи воспользуемся формулой для начисления сложного процента FV=PV(1+r)n При начислении сложного процента будущую стоимость находим путем умножения текущей стоимости на (1 + процентная ставка в долях) столько раз, на сколько лет (периодов) делаем расчет (будущая стоимость FV (англ. future value); текущая стоимость РV (англ. present value); процентная ставку – r, число лет (периодов) – п): FV = 9000 × (1+0,09)2 = 9000 × 1,1881=10692,9 Ответ: В результате инвестиций в сумме 9000 долларов под 9% годовых через два года получим 10692,9 долларов. Задача№2 Условие задачи: Рассчитайте текущую стоимость будущего дохода, который составит через три года 93,17 тыс. руб. при годовой ставке 10%. Решение: Для расчета воспользуемся формулой дисконтирования. Текущую стоимость находим путем деления будущей стоимости на (1 + процентная ставка) столько раз, на сколько лет (периодов) делаем расчет (будущая стоимость FV (англ. future value); текущая стоимость РV (англ. present value); процентная ставку – r, число лет (периодов) – п). В нашем случаем: РV = 93170 / (1 + 0,1)3=93100 / 1,331 = 70000 Ответ: Текущая стоимость будущего дохода, который составит через три года 93,17 тыс. руб. при годовой ставке 10% составляет 70000 рублей. Решите самостоятельно: Задача №1 Рассчитайте текущую стоимость будущего дохода, который составит через два года 93,17 тыс. руб. при годовой ставке 16%. Задача№2 Рассчитайте будущую стоимость сегодняшних инвестиций в сумме 120 000 рублей, которая будет получена через два года при 15% годовых. Задача №3 Два года назад коллекционер приобрел картину известного мастера. Ее сегодняшняя стоимость составляет 90506 долл. Рассчитайте цена ее покупки, если картина дорожала на 18% в год. Задача №4 Рассчитайте будущую стоимость сегодняшних инвестиций в сумме 120 000 рублей, которая будет получена через год при ставке процента 12% годовых при условии начисления процентов ежеквартально. Задача №5 Два года назад коллекционер приобрел картину известного мастера. Ее сегодняшняя стоимость составляет 86400 долларов. Рассчитайте цена ее покупки, если картина дорожала на 20% в год. Задача №6 Рассчитайте будущую стоимость сегодняшних инвестиций в сумме 12 000 долларов, которая будет получена через два года при 6% годовых. Задача №7 Три года назад коллекционер приобрел редкую монету. Ее сегодняшняя стоимость составляет 76043,75 рублей. Рассчитайте цена ее покупки, если монета дорожала на 15% в год. Задача №8 Рассчитайте будущую стоимость сегодняшних инвестиций в сумме 90 000 рублей, которая будет получена через два года при 16% годовых. Задача №8 Три года назад коллекционер приобрел редкую монету. Ее сегодняшняя стоимость составляет 70240,32 рублей. Рассчитайте цена ее покупки, если монета дорожала на 16% в год. Задача №10 Рассчитайте будущую стоимость сегодняшних инвестиций в сумме 100 000 рублей, которая будет получена через два года при 16% годовых при условии начисления процентов ежеквартально. Тема «Социальная политика» Пример решения ситуационной задачи: Задача№1 Условие задачи: Известно, что 20% наименее обеспеченного населения получают 5% доходов общества, а 20% наиболее обеспеченного населения — 60%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Решение: Построим по имеющимся данным кривую Лоренца: 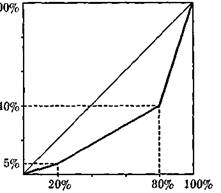 Значение коэффициента Джини равно отношению площади, ограниченной линией абсолютного равенства и реальным положением кривой Лоренца, к площади треугольника. Чтобы вычислить коэффициент Джини, найдем площадь фигуры под кривой Лоренца: Площадь заштрихованной части: 0,5 х 5 х 20 + 0,5 х (40 + 5) х 60 + 0,5 х (100 + 40) х 20 = 2800. Площадь треугольника равна: 100 х 100 х 0,5 = 5000. Значение коэффициента Джини составит: (5000 - 2800)/5000 = 0,44. Это минимальное значение коэффициента Джини, которое не учитывает весьма вероятного неравенства в распределении дохода внутри трех больших групп (нижних — 20%, средних — 60% и верхних — 20%). Задача №2 Условие задачи: Известны следующие данные о величине доходов равных групп населения города Н.: 1 группа – 3 тыс. руб.; 2 группа – 8 тыс. руб.; 3 группа – 14 тыс. руб.; 4 группа – 25 тыс. руб. Также известно, что 1 группа и 2 группа уплачивают 12% в качестве подоходного налога, 3 – 25% и 4 группы – 30%. Постройте кривую Лоренца до уплаты налогов для этих групп населения. Покажите новую кривую Лоренца схематически на графике. Стало ли распределение налогов более равномерным? Решение задачи: 1) Определить объем дохода в %: Размер совокупного дохода населения города составит: 3 + 8 + 14 + 25 = 50 (тыс. руб.) Если принять сумму совокупного дохода за 100%, то 1 группа (25% самого «бедного» населения) получает 6% всех доходов, 2 группа – 16%, 3 группа – 28%, 4 группа (25% самого «богатого» населения) – 50%. Используя эти данные, можем построить кривую Лоренца. Так как оплата налогов осуществляется по различным налоговым ставкам, и эти ставки возрастают с увеличением дохода, то нетрудно догадаться, что здесь используется прогрессивное налогообложение. Следовательно, после выплаты налогов распределение доходов среди жителей этого города будет чуть более равномерным. 2) Определим сумму совокупных доходов населения после налогообложения: (3 – 3×0,12) + (8 – 8×0,12) +(14 – 14×0,25) +(25 – 25×0,3) = 2,64 + 7,04 + 10,5 + 17,5 = 37,68 (тыс. руб.). Если принять сумму совокупного дохода после уплаты налогов за 100%, то 1 группа получает 7,0% всех доходов, 2 группа – 18,7%, 3 группа – 27,9%, 4 группа – 46,4%. Поэтому новая кривая Лоренца будет расположена чуть ближе к прямой абсолютногоравенства, чем кривая до уплаты налогов. Решите самостоятельно: Вариант 1 Известно, что 20% наименее обеспеченного населения получают 10% доходов общества, а 20% наиболее обеспеченного населения – 60%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 2 Известно, что 20% наименее обеспеченного населения получают 8% доходов общества, а 20% наиболее обеспеченного населения – 50%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 3 Известно, что 20% наименее обеспеченного населения получают 7% доходов общества, а 20% наиболее обеспеченного населения – 70%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 4 Известно, что 20% наименее обеспеченного населения получают 5% доходов общества, а 20% наиболее обеспеченного населения – 60%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 5 Известно, что 20% наименее обеспеченного населения получают 15% доходов общества, а 20% наиболее обеспеченного населения – 50%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 6 Известно, что 25% наименее обеспеченного населения получают 5% доходов общества, а 10% наиболее обеспеченного населения – 60%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 7 Известно, что 30% наименее обеспеченного населения получают 15% доходов общества, а 20% наиболее обеспеченного населения – 45%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 8 Известно, что 25% наименее обеспеченного населения получают 5% доходов общества, а 20% наиболее обеспеченного населения – 50%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 9 Известно, что 10% наименее обеспеченного населения получают 5% доходов общества, а 10% наиболее обеспеченного населения – 40%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? Вариант 10 Известно, что 20% наименее обеспеченного населения получают 10% доходов общества, а 15% наиболее обеспеченного населения – 50%. По имеющимся данным вычертите кривую Лоренца и определите значение коэффициента Джини. Является ли это значение верхней или нижней границей по сравнению с ситуацией, когда мы обладаем более полной информацией о распределении доходов? ОТВЕТЫ НА ТЕСТОВЫЕ ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ ВНЕАУДИТОРНОЙ РАБОТЫ Тема 1.
Тема 2.
Тема 3.
Тема 4.
Тема 5.
|
