учет погрешностей приблеженых значений. учет погрешностей приближенный значений. Учёт погрешностей приближённых вычислений
 Скачать 73.82 Kb. Скачать 73.82 Kb.
|
|
Министерство науки и высшего образования Российской Федерации. Институт ядерной энергетики (филиал) ФГАОУ ВО СПбПУ «Санкт-Петербургский политехнический университет Петра Великого» в г. Сосновый Бор  Кафедра « Проектирование и эксплуатация атомных станций» САМОСТОЯТЕЛЬНАЯ РАБОТА №1 По дисциплине: “Математические методы моделирования физических процессов” Тема: “Учёт погрешностей приближённых вычислений” Выполнил студентка гр.1951402/80001 ______________ (Калинина Т.А.) (подпись) Проверил (преп.) ………………. _____________ (Крюков Ю.В.) (подпись) «___» ____________2021 г. Г. Сосновый Бор 2 Вариант. Определить предельную абсолютную погрешность числа a=1.41,заменяющего иррациональное число 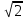 Решение: Первый способ: 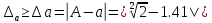 Воспользуемся неравенством : 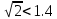 2 2Поскольку A= 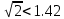 , то , то 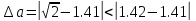 =0.01, т.е. =0.01, т.е. 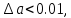 следовательно, в качестве величины следовательно, в качестве величины 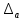 можно принять значение можно принять значение 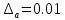 Если воспользоваться более точным неравенством для числа A= 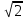 , т.е. , т.е. 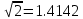 , то можно получить оценку величины , то можно получить оценку величины 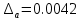 Второй способ: Величину a = 0.0042 можно получить, понимая, что число а = 1.41 может быть получено при округлении (в узком смысле) до трёх значащих цифр числа 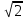 1.414213562373095. Поэтому предельная погрешность округления (отличающая а от 1.414213562373095. Поэтому предельная погрешность округления (отличающая а от 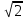 ) ≤ 0.0042, т.е. a = 0.0042 ) ≤ 0.0042, т.е. a = 0.0042 Ответ: 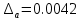 Дано приблеженное число a=10000, полученное при округлении по дополнению. Пользуясь формулой 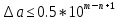 определить абсолютную погрешность данного числа. определить абсолютную погрешность данного числа.Решение: По алгоритму любое число может быть представлено виде десятичной дроби, поэтому для числа а=10000 справедлива запись 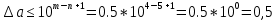 , где m=4,n=5 , где m=4,n=5Ответ: 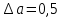 Дано приближенное число а=23.825 и известно, что у этого числа четыре верных значащих цифры в широком смысле( в узком смысле). Оценить абсолютную и относительную погрешность числа а в обоих случаях. Решение: Оценка абсолютной погрешности: Абсолютная погрешность данного числа не превосходит половины единицы десятичного разряда последней верной значащей цифры. Поэтому для числа а=23.825 имеем: 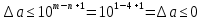 ,01 где m=1-старший десятичный разряд числа а, n=4-число верных значащих цифр ( для широкого смысла). ,01 где m=1-старший десятичный разряд числа а, n=4-число верных значащих цифр ( для широкого смысла).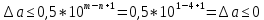 ,005 (для узкого смысла). ,005 (для узкого смысла).Оценка относительной погрешности: Для n верных значащих цифр в широком смысле: 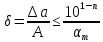 . .Поэтому для данного примера ( 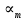 =3- цифра, соответствующая старшему десятичному разряду числа а, n=4) соответственно имеем: =3- цифра, соответствующая старшему десятичному разряду числа а, n=4) соответственно имеем: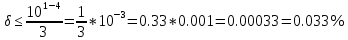 В узком смысле: 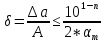 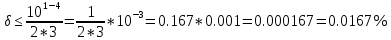 Ответ: 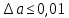 -абсолютная погрешность (в широком смысле) -абсолютная погрешность (в широком смысле) 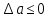 ,005- абсолютная погрешность ( в узком смысле) ,005- абсолютная погрешность ( в узком смысле)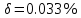 -относительная погрешность ( в широком смысле) -относительная погрешность ( в широком смысле)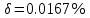 - относительная погрешность ( в узком смысле) - относительная погрешность ( в узком смысле)Дано приближенное число а=1,182 и известно, что его абсолютная погрешность равна 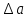 =0,003. Определить, какие значащие цифры приближенного числа будут верными в широком( в узком) смысле. =0,003. Определить, какие значащие цифры приближенного числа будут верными в широком( в узком) смысле.Решение: По определению верных значащих цифр приближенного числа единица десятичного разряда, соответствующего верной значащей цифре числа должны быть не меньше его погрешности. То есть если числа а имеет n верных значащих цифр, то для него выполняется неравенство: 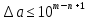 , m=0- старший десятичный разряд числа а. Следовательно, , m=0- старший десятичный разряд числа а. Следовательно, 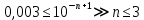 - в широком смысле. - в широком смысле.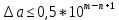 = =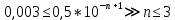 - в узком смысле. - в узком смысле.Ответ: При абсолютной погрешности 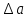 =0,003 у приближенного числа 1,182 должно быть не более 3 значащих цифр. =0,003 у приближенного числа 1,182 должно быть не более 3 значащих цифр.Со сколькими верными значащими цифрами в широком(узком) смысле следует вычислить cos32˚, чтобы: Абсолютная погрешность результата не превышала 0,001; Относительная погрешность результата не превышала 5%; Решение: А)При вычисление cos32˚получаем: cos32˚=0.85 Абсолютная погрешность полученного приближенного числа а будет удовлетворять соотношению: 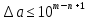 Согласно условию задачи необходимо, чтобы: 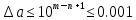 Старший десятичный разряд m=-1,то 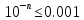 Для узкого смысла: 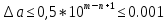 = = 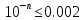 Ответ: для того чтобы при округлении числа cos32˚ абсолютная погрешность полученного результата не превышала 0,001 при округлении по усечению необходимо сохранить 3 значащих цифры. Б) воспользуемся формулой для n верных значащих цифр в широком смысле 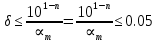 Для числа а=cos0.32˚ первая цифра 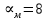 , поэтому окончательно получаем , поэтому окончательно получаем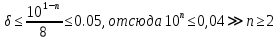 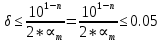 -для узкого смысла -для узкого смысла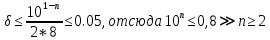 Ответ: для того чтобы при округлении числа cos32˚ относительная погрешность полученного результата не превышала 5% при округлении необходимо сохранить как минимум 2 цифры. Вычислить значение функции, округлив значения ее аргументов до четырех значащих цифр( в узком смысле). Оценить абсолютную погрешность вычисленного значения. y=lg(cos(32◦)+√e·tg(5) ; Решение:𝑦=lg(𝑐𝑜𝑠32°)+√𝑒∗𝑡𝑔5 Заменим cos32˚=x1; e=x2; tg5=x3 Тогда:𝑦(𝑥1,𝑥2,𝑥3)=𝑙𝑔𝑥1+√𝑥2∗𝑥3 Округлим значения аргументов до четырех значащих цифр в узком смысле:x1=0.8480, x2=2.718,x3=-3.381;∆x1=0.00005,∆x2=0.0005,∆x3=0.005 Получим y(x1,x2,x3)=-5.645642 ∆𝑦≤𝑏1∗∆𝑥1+𝑏2∗∆𝑥2+𝑏3∗∆𝑥3 𝑏1= 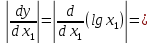 0.512134 0.512134𝑏2 = 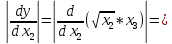 1.0254 1.0254𝑏2= 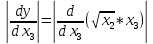 1.65 1.65∆𝑦≤0.512134∗0.00005+1.0254∗0.0005+1.65∗0.005=0.0014 Ответ: абсолютная погрешность вычисленного значения функции равна y=-5.646±0.0014 7.С каким количеством верных знаков следует взять значение аргументов функции (1), чтобы значение этой функции имело четыре верных знака (задачу решить в рамках предположения о равенстве абсолютных погрешностей аргументов). Решение: Погрешность определяется из соотношения: 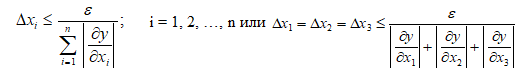 Выясним значение ɛ для функции 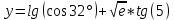 Известно, что 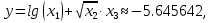 тогда m=0,n=4. тогда m=0,n=4.Тогда = y 0.510 m n+1 ≥ 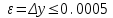 Решим обратную задачу теории погрешностей. 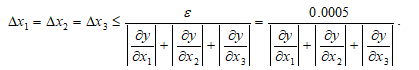 Значения величин возьмем из 6 задания. 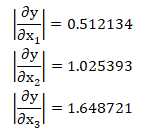 Δx1= Δx2= Δx3≤ 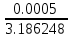 ≈1.6·10-4 ≈1.6·10-4 Следовательно , Δxi≤1.6·10-4 погрешности округления 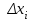 приближённых аргументов xi всегда удовлетворяют неравенству Δxi=0.5·10m-n+1, определим количество верных десятичных знаков. приближённых аргументов xi всегда удовлетворяют неравенству Δxi=0.5·10m-n+1, определим количество верных десятичных знаков. X1= 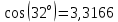 , X2= , X2=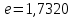 , X3= , X3=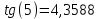 Для этих чисел m=0, то 0.5·10-n+1≤1.6·10-4, следовательно n 5 Ответ: функция будет иметь 4 верных знака при условии, что приближенные значения мы округлим до 5 верных десятичных знаков. |
