Учитель математики
 Скачать 399 Kb. Скачать 399 Kb.
|
|
Главные условия успешности проблемного обучения: обеспечение достаточной мотивации, способной вызывать интерес к достижению проблемы; обеспечение посильной работы с возникающими на каждом этапе проблемами; значимость информации, получаемой при решении проблемы для обучаемого; необходимость доброжелательного диалогического общения педагога с учащимися, когда ко всем мыслям, гипотезам, высказываниям учащегося относятся с вниманием и поощрением. Главные цели проблемного обучения: развитие мышления и способностей учащихся, развитие творческих умений; усвоение учащимися знаний и умений, добытых в ходе активного поиска и самостоятельного решения проблем, в результате эти знания, умения более прочные, чем при традиционном обучении; воспитание активной творческой личности учащегося, умеющего видеть, ставить и разрешать нестандартные проблемы. Современные исследования показывают, что в классах, где проводятся проблемные уроки, количество знаний на 20% выше, чем в традиционном обучении. Средством реализации проблемного обучения, кроме задач и вопросов, становятся методы проблемного обучения. Методы проблемного обучения различаются степенью возрастания сложности и самостоятельности учащихся при разрешении учебных проблем: - проблемное изложение знаний - изложение с проблемным началом - частично-поисковый, или эвристический метод - исследовательский метод Методические приёмы создания проблемной ситуации 1. Подведение обучаемых к противоречию с предложением самим найти способ разрешения. 2. Изложение различных точек зрения на один и тот же вопрос . 3. Предложение обучаемым рассмотреть один и тот же вопрос с различных позиций. ( юриста, учителя, художника и т.д.) 4. Побуждение обучаемых делать сравнения, обобщения, выводы, сопоставлять факты. 5. Постановка задач с заведомо допущенными ошибками. Проблемность при обучении математики возникает совершенно естественно, не требуя никаких специальных упражнений, искусственно подбираемых ситуаций. В сущности, не только каждая текстовая задача, но и добрая половина других упражнений, представленных в учебниках математики и дидактических материалах, и есть своего рода проблемы, над решением которых ученик должен задуматься, если не превращать их выполнение в чисто тренировочную работу, связанную с решением по готовому, данному учителем образцу. Учитель нередко наносит ущерб делу, разучивая с детьми способы решения задач определенных видов, предлагая подряд большое число однотипных упражнений, каждое из которых, будучи предъявлено среди упражнений других видов, без дополнительных объяснений, могло бы послужить для отталкивания собственной мысли учащихся. Упражнения в решении составных текстовых задач, в сравнении выражений, требующие использования известных детям закономерностей и связей в новых условиях, упражнения геометрического содержания, которые часто требуют переосмысления приобретенных ранее знаний, и другие должны быть использованы для постановки детьми проблемных задач. Самостоятельность мышления ставит ученика перед определенными трудностями, требующими значительного умственного усилия при выполнении мыслительных операций, приводящих к решению. Проблемные задачи ставят ученика в ситуацию, в которой у него должно появиться удивление и ощущение трудности, или одно только ощущение трудности, которое, однако, ученик намерен преодолеть. Если эти условия отсутствуют, то задача или уже перестала быть для него проблемной, или еще не может быть ею в связи с тем, что он не владел в достаточной степени средними ступенями, дающими возможности для преодоления данной трудности. Психолог В.А. Крутецкий приводит типы задач для развития активного самостоятельного, творческого мышления. Знание учителем этой типологии - важное условие создания проблемных ситуаций при изучении нового материала. Вот некоторые из них: - задачи с не сформулированным вопросом; - задачи с недостающими данными; - задачи с излишними данными; - задачи с несколькими решениями; - задачи с меняющимся содержанием; - задачи на соображение, логическое мышление. Таким образом, постановка вопроса об использовании проблемных ситуаций не является новой для учителя, а требуют лишь правильного использования всех тех ресурсов, которые скрыты в курсе математики. Только в этом случае обучение математике будет оказывать действенную помощь в решении образовательных, воспитательных и развивающих задач обучения, способствуя развитию познавательных способностей учащихся, таких черт личности, как настойчивость в достижении поставленной цели, инициативность, умение преодолевать трудности. 4.Результативность работы В заключение можно сказать, что метод проблемного обучения является одним из важных направлений учебного процесса, потому что он способствует активизации познавательной деятельности учеников, придает их учебным работам творческий характер, создавая благоприятные условия для индивидуального развития учеников, развивая их мышление. Я согласна с высказыванием известного психолога С.Л. Рубинштейна, о том, что «мышление обычно начинается с проблемы или вопроса…» и считаю, что проблемному обучению надо предоставить значительное место в процессе изучения математики. Педагогическими преимуществами проблемного изложения знаний по сравнению с традиционным является следующее: Проблемное обучение делает изложение более доказательным , а знания более осознанными и тем способствует превращению знаний в убеждения. Проблемное обучение учит мыслить научно, диалектически, дает учащимся эталон научного поиска. Проблемное обучение более эмоционально, а потому оно повышает интерес к учению. Проблемный путь получения знаний требует больших затрат времени, чем сообщение готовой информации, нельзя полностью перейти на проблемное обучение. Не всякий материал может служить основой для создания проблемной ситуации. К непроблемным относится информация, которую нельзя «открыть»: аксиомы, изучение сложных тем, где необходимо объяснение учителем, а самостоятельный поиск оказывается недоступным для большинства школьников. В обучении всегда будут нужны и тренировочные задачи, и задания, требующие воспроизведения знаний, способствующие запоминанию необходимого. Я считаю, что для достижения результатов необходимо грамотно сочетать традиционное обучение с созданием проблемных ситуаций. Работая по данной технологии, внедряю в процесс проблемного обучения игровые технологии, дифференцированное обучение. Свою работу мне хочется закончить строками Б.Пастернака: Во всем мне хочется дойти До самой сути. В работе, в поисках пути, В сердечной смуте. До сущности протекших дней, До их причины, До оснований, до корней, До сердцевины. Следуя этим словам, можно в любой деятельности найти её корень, сердцевину, а учителю увидеть в каждом ребенке индивидуальность и развить её. Приложения. Приложение 1 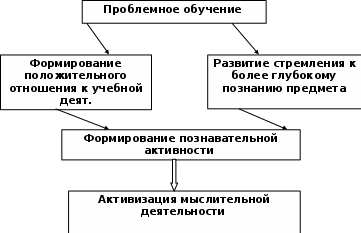 Приложение 2 Как провести проблемный урок? Проблемные уроки проводятся по следующей схеме: Учитель ставит для всех общую проблему, формулируя последовательно на всех уровнях проблемности, начиная с самого высокого. (Чтобы определить, кто в состоянии вывести правило на каждом из четырех уровней проблемности, как ученик шел к открытию правила). Учащиеся фиксируют результаты своих попыток вывести правило, записать его на листочках, ставя порядковый номер проблемности. (Это дает возможность учителю контролировать работу каждого ученика на всех этапах вывода правила. Если учащиеся выводят и фиксируют правило на самом высоком или последующих уровнях проблемности кроме низкого, они и в дальнейшем должны продолжать работу над правилом: проверять формулировку в соответствии с показами и, если нужно, уточнять и совершенствовать ее. В случае, когда отдельные ученики не справляются с заданием ни на одном уровне проблемности, учитель имеет возможность определить характер затруднений, их причины и своевременно помочь; вместе с тем он имеет возможность формировать у детей соответствующие операции, развивать творческое мышление). Учитель спрашивает некоторых из учащихся (после того как учащиеся записывают формулировку правила при постановке задания на низком уровне проблемности), какое они правило вывели, просит произнести это правило в их формулировке. Учитель формулирует правило так, как оно дано в учебнике. Сообщает, какое правило изучено, записывает тему на доске. Закрепление знаний и формирование умений и навыков проводится в форме письменного и устного выполнения упражнений из учебника. Такая организация работы отнимает немало времени, однако она рациональна: все дети, используя помощь учителя, должны думать и писать, совершенствуя формулировку; учитель имеет возможность проанализировать попытки, ход открытия правила каждым учеником, то есть выявить индивидуальные особенности мыслительной деятельности; каждый ученик убеждается в том, что если будет внимательным, подумает, применит имеющиеся знания, то обязательно справится с заданием; подсказки учителя направляют мысль ученика, помогают овладеть мыслительными операциями: сравнением, анализом, синтезом, обобщением, при этом ученики, которые овладели мыслительными операциями, упражняются в них, а другие обучаются им постепенно; воспитываются ценные качества личности – способность к напряженному умственному труду, самостоятельность, пытливость, трудолюбие; формулируется математическая зоркость, устойчивость, устойчивые математические навыки, развивается творческое мышление. При такой организации проблемного урока нет изначального деления учащихся на «сильных», «средних» и «слабых» - задание всем одинаковое; конечный результат – формулировка правила на одном из уровней проблемности – показатель уровня самостоятельности и развития мыслительной деятельности, уровня развития творческого мышления учащихся. Приложение 3 Анализ возможностей использования проблемного обучения на уроках математики
Приложение 4 Игровые технологии, используемые на проблемном уроке Интеллектуальный марафон (математика, 5 класс) 1. Если буквы слова "кенгуру" расположить в алфавитном порядке, какая буква окажется на третьем месте? 1) К 2) Е 3) Н 4) Г 5) Р 2. Сутки на планете Тамагочи на 40 минут длиннее, чем на планете Земля. На сколько неделя на Тамагочи отличается от недели на Земле? 1) 4 ч 40 мин 2) 2 ч 20 мин 3) 7 ч 20 мин 4) 40 мин 5) 28 ч 3. Решите анаграммы: 1) чадаза 2) гурк 3) чул 4) мапряя 4. Расшифруйте "закодированные" слова: 1) и100рия 2) про100р 3) кис. 4) 3тон 5) о3цание 5. Вставьте пропущенное число: 1.
2.
6. Вычислите площадь квадрата, периметр которого равен 36 см2 1) 12 см2 2) 18 см2 3) 81 см2 4) 36 см2 5) 25 см2 7. Выберите самое маленькое четырехзначное число, в записи которого все цифры разные. 1) 1023 2) 1234 3) 1203 4)1032 5) 1203 Интеллектуальный марафон (математика, 6 класс) Oпределите дату исторического события Решите анаграммы и исключите лишнее слово: НОЕБДРО, ЗАКОПАТЕЛЬ, ЛОЕЦЕ, ПЕНЬСТЕ Вставьте пропущенное число:
Лошадь съедает копну сена за 2 суток, корова – за 3, овца – за 6 суток. За какое время съедят копну сена лошадь, корова и овца вместе? 1) 1/2суток 2) 1 сутки 3) 2 суток 4) 1/4суток 5) 1,5 суток Число 2,4 увеличили на 25%. На сколько процентов нужно уменьшить полученное число, чтобы вновь получить 2,4? 1) 25% 2) 15% 3) 20% 4) 22% 5) 19% Вставьте пропущенное слово:
Какое из данных чисел чаще других встречается в таблице умножения? 1) 36 2) 42 3) 56 4) 64 5) 27 Найдите закономерность в образовании чисел и вставьте пропущенные числа:
Приложение 5 Примеры проблемных ситуаций, используемые на уроках математики 1. Создание проблемных ситуаций через умышленно допущенные учителем ошибки. В понимании детей учитель – это компьютер, который не может ошибиться никогда, и они обычно слепо копируют его решение. Пример №1. Тема «Линейные уравнения с одной переменной». (7 класс) Решаю быстро уравнение: (3Х + 7) · 2 – 3 = 17 6Х + 14 – 3 = 17 6Х = 17 – 14 – 3 6Х = 0 Х = 0 Естественно при проверке ответ не сходится Проблемная ситуация. Ищут ошибку. Дети решают проблему. После этого учащиеся очень внимательно следят за мыслью и решением учителя. Результат - внимательность и заинтересованность на уроке. Пример №2. Даю задачу на дом и говорю: “У меня не получается”. Попробуйте вы, обращайтесь к кому хотите за помощью. Хотя задача решается. Проблемная ситуация. На другой урок у них радостные лица – они решили. Вот такие примеры активизируют деятельность учащихся. Пример №3. «Обманные задачи»: а) Постройте прямоугольник со сторонами 2, 3 и 5 см. б) Больший угол треугольника равен 50°. Найдите остальные углы. в) Две стороны треугольника перпендикулярны третьей. Определите вид треугольника. г) Внешний угол при основании равнобедренного треугольника равен 75°. Найдите углы треугольника. д) Диагональ ромба в два раза больше его стороны. Найдите углы ромба. 2.Создание проблемных ситуаций через использование занимательных заданий. Пример №1. Тема: «Линейная функция»(7 класс) Обычная форма задания: функция задана формулой 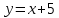 найдите значение функции при x = 0, 7, -5, 1. найдите значение функции при x = 0, 7, -5, 1.Занимательная форма задания: Приглашаю к доске ученика, даю ему карточку, на которой написано. 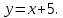 На доске заготовлена таблица: На доске заготовлена таблица:
Ученик из класса называет какое-нибудь значение х. Ученик у доски вписывает это число в таблицу и, поставив его в формулу, находит и вписывает в таблицу соответствующее ему значение у. Затем другой ученик из класса называет другое значение х и ученик у доски проделывает те же операции. Задача класса – “угадать” формулу, записанную на карточке. Проблемная ситуация создана. Выигрывает тот ученик, который первый назовет формулу. Пример №2. Тема: «Координатная плоскость» (6 класс) В начале урока учитель демонстрирует классу хорошо знакомые предметы, например, шахматную доску, глобус, билет в театр. Учащимся предлагается ответить на вопрос: «Что объединяет все эти предметы?». Поиск ответа можно начать с чтения отрывка из первой главы романа Ж. Верна «Дети капитана Гранта». После окончания чтения учитель выстраивает подводящий диалог: Почему героям романа пришлось преодолеть столько километров пути в поисках пропавшей экспедиции? – Не известно точное местонахождение героев. Как в географии описывается точно местонахождение объекта? – Указываются широта и долгота (географические координаты). Что же общего у предметов, которые были предъявлены вам в начале урока? – Они позволяют определить положение (место) человека в зрительном зале или фигуры на шахматной доске. Затем учитель предлагает вернуться к математике и попробовать провести параллель между объектами в географии и математике. Как описать положение точки на плоскости? – Ввести координаты на плоскости. Какова же тема урока? - Координаты на плоскости. (На доске появляется тема урока) Географические координаты (широта и долгота) – это воображаемые окружности на поверхности земного шара. Что можно взять на плоскости вместо окружностей? – Прямые. Сколько прямых и каково их взаимное расположение? – Две пересекающиеся прямые. В заключение диалога учитель подводит итог: «Наверное, таким же образом рассуждал ещё один великий француз – Рене Декарт, когда предложил использовать две взаимно перпендикулярные прямые для введения координат на плоскости. С тех пор математики всего мира так и говорят – декартова система координат». (На слайде демонстрируется портрет Декарта) Далее на уроке рассматриваются типовые задачи (нахождение координат точки и построение точки по заданным координатам) и выполняется задание «Рисуем по координатам». В качестве домашнего задания можно предложить учащимся творческую работу «Зашифруй рисунок», а также привести примеры из повседневной жизни, где мы встречаемся с координатами на плоскости (артиллерия, домашний адрес). Пример № 3. Тема: «Теорема, обратная теореме Пифагора» (8 класс) Урок начинается с рассказа о египетском треугольнике. Развитие геометрии было связано в том числе и с потребностями строительной техники. Так, еще древним египтянам требовалось умение строить прямой угол. Этим занимались работники – «натягиватели веревки», которые назывались так потому, что построение осуществлялось с помощью веревки с завязанными узелками, длина которой равнялась (3+4+5) единиц. В землю вбивались три кола, на которые и натягивалась веревка, так чтобы получился треугольник со сторонами 3, 4 и 5 единиц. Египтяне знали, что угол между меньшими сторонами будет прямым. Такой треугольник в математике до сих пор называется египетским. (На доске – рисунок прямоугольного треугольника со сторонами 3, 4 и 5 единиц) Учитель предлагает классу убедиться в верности построений древних египтян с помощью теоремы, обратной теореме Пифагора. В данный момент урока уместно еще раз вспомнить: о строении любой теоремы (Дано – доказать; Условие – заключение), о связи между формулировками прямой и обратной теорем (условие и заключение теорем «меняются местами»), формулировку теорему Пифагора. А затем попросить учащихся самостоятельно сформулировать обратную теорему. Обычно учащиеся дают следующую формулировку: «Если квадрат гипотенузы равен сумме квадратов катетов, то треугольник прямоугольный». В ходе беседы выясняем, что: использовать термины «катет» и «гипотенуза» нельзя, вспоминаем, что гипотенуза – большая сторона прямоугольного треугольника, заменяем слово «гипотенуза» словами «большая сторона», а «катеты» - на слова «две другие стороны». Учащиеся корректируют данную ими ранее формулировку теоремы и получают: «Если квадрат большей стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный». Осталось только воспользоваться данной формулировкой, чтобы убедиться в том, что треугольник со сторонами 3, 4 и 5 будет действительно прямоугольным. Пример №4. Тема: «Теорема Виета» (8 класс) Урок начинается с исторической зарисовки (на слайде – портрет Франсуа Виета). XVI век. Франция. Адвокат и советник короля Генриха III Франсуа Виет, будучи выдающимся математиком, сумел раскрыть ключ шифра, состоявшего из 500 знаков, с помощью которого враги короля вели переписку с испанским двором. Но среди математиков Виет известен своей теоремой о свойствах корней квадратного уравнения. Далее учащимся предлагаются задания: 1) Запишите данные уравнения в тетрадь и подчеркните те из них, которые имеют общее отличие от остальных. Укажите это отличие. а) - 5х 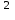 - 6х + 1 = 0; б) 6d - 6х + 1 = 0; б) 6d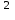 - 5d – 1 = 0; в) х - 5d – 1 = 0; в) х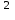 - 5х + 6 = 0; - 5х + 6 = 0;г) 7х 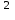 - 6х + 2 = 0; д) z - 6х + 2 = 0; д) z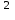 + 8z + 15 = 0; е) t + 8z + 15 = 0; е) t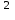 - 3t – 4 = 0. - 3t – 4 = 0.После выполнения этого задания даем определение приведенного квадратного уравнения, записываем его в общем виде, вводим обозначение коэффициентов. 2) Решите приведенные квадратные уравнения и найдите сумму и произведение корней. На доске записываем только условие приведенного квадратного уравнения, сумму и произведение корней:
3) Сравните полученные числа и коэффициенты! Что интересного вы заметили? Запишите это свойство для уравнения х 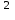 + px + q = 0. + px + q = 0.На слайде: х 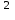 + px + q = 0 + px + q = 0х 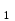 + х + х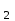 = - p, = - p,х 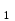 · х · х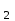 = q = qДалее учитель подводит итог работы: именно эту зависимость для любого квадратного уравнения и увидел Франсуа Виет. На слайде: ax 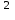 + bx + c = 0 | :a + bx + c = 0 | :ax 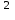 + + 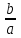 x + x + 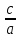 = 0 = 0Теорема Виета для квадратного уравнения общего вида: х 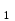 + х + х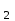 = - = - 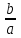 , ,х 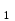 · х · х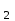 = = 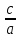 Звучат стихи Александра Гуревича , посвященные теореме Виета: По праву достойна в стихах быть воспета О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого? Умножишь ты корни – и дробь уж готова, В числителе «с», в знаменателе «а». А сумма корней тоже дроби равна, Хоть с минусом дробь эта, что за беда? В числителе «b», в знаменателе «а»! Пример №5. Тема: «Формулы сокращённого умножения»(7 класс) Преступники украли в банке большую сумму денег. Их поймали, но похищенную сумму установить не удалось. Преступники категорически отказываются назвать её, утверждая, что записали это число в виде степени и зашифровали не только основание, но и её показатель. Экспертам удалось узнать основание степени. Это число 597. Но каким был показатель не говорят. После очередного допроса преступники сказали, что показатель степени является корнем уравнения ( 2y +1)2 – 4y2 =9 y = 2 5972 = (600 – 3)2 =6002 -2 · 600 · 3 + 32 = 360000 – 3600 + 9 =356409 Пример №6. Тема «Сумма n-первых членов арифметической прогрессии» (9 класс) Начать урок можно с исторической зарисовки о детстве великого математика Карла Гаусса. Рассказывают, что в начальной школе, где учился мальчик Карл Гаусс, ставший потом знаменитым математиком, учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал детям задание - вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Он увидел, что… На доске: 1 + 2 + 3 + …+ 98 + 99 + 100 = (1+100)+(2+99)+(3+98)+…+(50+51) = 101·50 = 5050 Подводящий диалог: Попробуем взглянуть на условие задачи с высоты наших знаний: Что собой представляет последовательность чисел 1, 2, …, 100? - Арифметическую прогрессию, первый член которой равен 1, n-член равен 100, а разность равна 1. Что требуется найти? - Сумму 100 первых членов. (Вводим обозначение. На доске: S 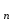 - сумма n-первых членов арифметической прогрессии). - сумма n-первых членов арифметической прогрессии).Какова будет тема урока? - Сумма n-первых членов арифметической прогрессии. На доске появляется тема урока и условие задачи: Дано: (a 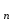 ) – арифметическая прогрессия, ) – арифметическая прогрессия,а 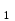 = 1, а = 1, а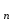 = 100, n = 100 = 100, n = 100Найти: S 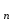 . .Попробуйте связать числа 101 и 50 с данными «нашей задачи». Что интересного вы заметили? - 101 = а 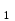 + а + а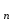 , 50 = , 50 = 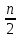 . .Запишите формулу суммы n-первых членов геометрической прогрессии. – S 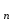 = (а = (а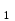 + а + а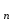 )· )·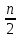 = = 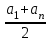 ·n ·n Существует еще одна формула суммы n-первых членов геометрической прогрессии, которую вы получите, если воспользуетесь формулой n-члена арифметической прогрессии а 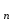 = а = а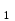 + (n – 1)·d. - S + (n – 1)·d. - S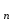 = = 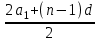 ·n ·n На доске появляются формулы: S 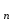 = (а = (а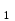 + а + а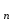 )· )·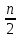 = = 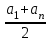 ·n (1) ·n (1)S 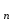 = = 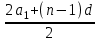 ·n (2) ·n (2)Главный фактор занимательности – это приобщение учащихся к творческому поиску, активизация их самостоятельной исследовательской деятельности, так как уникальность занимательной задачи служит мотивом к учебной деятельности, развивая и тренируя мышление вообще и творческое, в частности. Пример №7 «Сумма n-первых членов геометрической прогрессии» (9 класс) Учитель начинает урок с индийской легенды об изобретателе шахмат. Рассказывают, что индийский царь Шерам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат: за первую клетку шахматной доски 1 зерно, за вторую – 2, за третью – 4, за четвертую – 8, и так до 64 клетки. Царь приказал немедленно выдать столь «ничтожную» по его мнению, награду, взяв зерно из кладовых дворца. Каково же было его удивление, когда на следующее утро он узнал, что в кладовых дворца нет требуемого количества зерен. Не оказалось его и во всем царстве Шерама! А мудрецы, которым царь велел исчислить требуемое количество зерен, утверждали, что если бы удалось засеять пшеницей площадь всей поверхности Земли, считая и моря, и океаны, и горы, и пустыни, и получить удовлетворительный урожай, то, пожалуй, лет за пять Шерам смог бы рассчитаться с просителем. Как вы считает – стоило ли ему смеяться? Какое же количество зерен потребовал изобретатель шахмат? Попробуйте и вы ответить на этот вопрос! (Учащимся дается 5 минут на решение задачи.) Побуждающий диалог: Вы смогли выполнить задание? В чем затруднение? – Нет. Очень долго считать. Какой возникает вопрос? – Нельзя ли упростить решение? Нет ли формулы? Давайте «переведем» содержание задачи на язык математики, чтобы понять какую формулу мы хотим получить. – Число зерен, которые потребовал мудрец за каждую клетку, образуют геометрическую прогрессию, в которой всего 64 члена (по числу клеток шахматной доски), первый член равен 1, а знаменатель 2. Нужно найти сумму n-первых членов. Какова же тема урока? - Формула суммы n-первых членов геометрической прогрессии. На доске появляется тема урока и условие задачи. Дано: (b 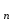 ) – геометрическая прогрессия, ) – геометрическая прогрессия,b 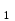 = 1, b = 1, b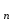 = 2 = 2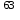 , q = 2, n = 64 , q = 2, n = 64Найти: S 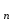 Далее учащиеся под руководством учителя выводят формулу суммы n-первых членов геометрической прогрессии. Пример №8.Тема «НОК и НОД» (6 класс) В легенде рассказывается, что, когда один из помощников Магомета – мудрец Хозрат Али садился на коня, подошедший человек спросил его: - Какое число делится без остатка на 2, 3, 4, 5, 6, 7, 8, 9? Мудрец ответил: - Умножь число дней в неделе на число дней в месяце (считая, что в месяце 30 дней) и на число месяцев в году. Прав ли Хозрат Али? Почему? 3. Создание проблемных ситуаций через решение задач, связанных с жизнью. Пример №1. Тема «Периметр прямоугольника»( 5 класс) Семья Димы летом переехала в новый дом. Им отвели земельный участок прямоугольной формы. Папа решил поставить изгородь. Он попросил Диму сосчитать сколько потребуется штакетника, для изгороди, если на 1 погонный м. изгороди требуется 10 штук? Сколько денег потратит семья, если каждый десяток стоит 50 рублей. Проблемная ситуация: нужно найти длину изгороди (периметр прямоугольника). Пример №2. Тема: «Площадь прямоугольника» ( 5 класс) На прошлом уроке ребята мы измеряли длину и ширину нашего класса и по формуле, нашли его периметр. Р= 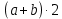 = (6+9)·2=30м. Помните! = (6+9)·2=30м. Помните!Посмотрите, пожалуйста, на пол. Линолеум износился, много чёрных полос. Вам нравится? Мне тоже не нравится. Я думаю, что летом нам нужно обязательно постелить новый линолеум. Давайте с вами посчитаем, сколько денег нужно будет собрать с каждого родителя на замену линолеума , если 1 погонный метр стоит 800 рублей. Проблемная ситуация. Для решения этой задачи нам нужно найти площадь пола (площадь прямоугольника). Пример №3. Тема «Проценты»( 5 класс) Вы знаете, что в этом году я награждена премией директора школы за высокие результаты в обучении. Конечно же, в этом и ваша заслуга. Спасибо. Размер премии 10 тыс. руб. Но я получу не все деньги. Вычитают подоходный налог 13%. Я хочу, чтобы вы помогли сосчитать, какую сумму я получу. Вопрос: «А как же мы вам поможем, если мы не знаем, что такое процент?» Проблемная ситуация создана. Ребята с удовольствием работают в течении всего урока. В конце урока дорешивают задачу до конца. Я вижу радостные лица ребят. Они справились с проблемой! Пример №4. Тема «Объем прямоугольного параллелепипеда». Длина плавательного бассейна 200 м, а ширина 50 м. В бассейн налили 2 000 литров воды. Как вы полагаете, можно ли плыть в этом бассейне? 4.Создание проблемных ситуаций через выполнение практических заданий. Пример №1. Тема «Площадь прямоугольника» .(5 класс) На уроке технологии Серёжа выпиливал лобзиком и получил различные остатки фанеры. В каком из остатков выбрасывается фанеры больше? 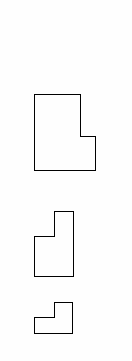 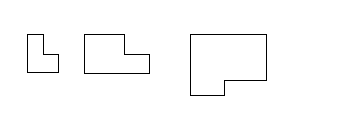  Проблемная ситуация. Нужно найти площадь данной фигуры. Вывод: разбить фигуру на прямоугольники, найти площадь каждой части и сложить (один из вариантов) Пример.№2. Тема «Площадь квадрата» (5 класс) К уроку вам было дано задание из газеты склеить 1 м2. Вы сделали это? Молодцы. Давайте посмотрим, сколько человек поместится на нём. Выясняем, что 4 человека. Как вы думаете, возможно ли на квадратной площадке со стороной 30 км. поместить всё население мира ?( 6,5 млрд.) Проблемная ситуация: нужно найти площадь площадки (площадь квадрата) Пример №3. Тема «Координатная плоскость» (6 класс) На этапе активного и осознанного усвоения нового материала, а также на этапе закрепления применяю практические работы «Животные на плоскости», «Астрономия и координатная плоскость». Ребята строят точки по координатам и рисуют животных и созвездия, затем рассказывают про них. Также выполняют творческие работы, сами предлагают свои рисунки и по ним составляют задания. Пример № 4.Темы: «Построение треугольника по трем элементам», «Неравенство треугольника».(7 класс) Теорему о неравенстве треугольника вводим при изучении темы «Построение треугольника по трем элементам», решая задачу на построение треугольника по трем его сторонам. Предлагаем ученикам построить с помощью циркуля и линейки треугольник со сторонами: а) 5см; 6см; 7см; б) 9см; 5см; 6см; в) 1см; 2см; 3см; г) 3см; 4см; 10см. Ребята работают самостоятельно и приходят к тому, что построить треугольник в последних двух примерах не удается. Возникает проблема: «При каких же условиях существует треугольник»? Чертежи, полученные учащимися при решении этой задачи, дают возможность легко сделать вывод: «Каждая сторона треугольника меньше суммы двух других сторон». Доказываем полученную теорему. 5. Создание проблемных ситуаций через решение задач на внимание и сравнение. Пример№1. Третьекласснице Даше учительница дала задание сосчитать, сколько треугольников изображено на рисунке. Она нашла 5 треугольников. Подошла Лена и нашла 7 треугольников. Кто из них прав? Попробуем посчитать вместе. Определите, сколько треугольников вы видите на рис.1 и квадратов на рис.2а, б? 2. Что общего в данных фигурах, а в чём различие? Пример №2.Тема: «Площадь трапеции». (8 класс) При выводе формулы для вычисления площади трапеции учитель предлагает учащимся воспользоваться ранее изученными формулами для вычисления площади прямоугольника, параллелограмма, треугольника, свойствами площадей. Ребята предлагают различные способы: а) провести диагональ и найти площадь трапеции как сумму площадей двух треугольников; б) провести две высоты и найти площадь трапеции как сумму площадей прямоугольника и двух прямоугольных треугольников; в) провести прямую, параллельную боковой стороне трапеции и найти площадь трапеции как сумму площадей параллелограмма и треугольника. Пример №3. Тема: «Четырехугольники». (8 класс) К моменту изучения темы «Квадрат» учащимся знакомы такие виды четырехугольников как прямоугольник, ромб и их свойства. Прошу учащихся сформулировать определение квадрата. На что они дают два разных определения: «Квадратом называется прямоугольник, у которого все стороны равны» или «Квадратом называется ромб, у которого все углы прямые». Оба определения верные. Обсуждаем, почему имеет право быть каждое из них. 6.Создание проблемных ситуаций через противоречие нового материала старому, уже известному. Пример№1. Тема «Формулы сокращённого умножения» (7 класс) Вычисляем (2 · 5)²= 2² ·5² = 100 (3 · 4)²= 3² · 4² = 9 · 16 = 144 (5 : 6)² = 5² : 6² = 25 : 36 (3 + 4)² = 3² + 4² = 9 + 16 = 25 Попробуйте сосчитать по-другому. ( 3 + 4)² =7² = 49 Проблемная ситуация создана. Почему разные результаты? ( 3 +4)² ≠ 3² + 4² 7. Создание проблемных ситуаций через различные способы решения одной задачи. Пример №1. Тема «Решение задач» (7 класс) На заправке села две цистерны. В начале посевной обе цистерны заполнены. В 1 было 59 т бензина, а во 2 - 44 т. Через сколько дней в цистернах останется одинаковое количество горючего, если ежедневно из 1 цистерны ежедневно расходуется 5т, а из 2 - 2 т. Решают с помощью уравнения (алгебраический) 59 – 5х = 44 – 2х А вот вчера четвероклассник Стас, который не умеет решать такие уравнения, тоже смог её решить. Проблемная ситуация: какой способ он предложил (арифметический) 8. Создание проблемных ситуаций через выполнение небольших исследовательских заданий. Пример№1. Тема «Длина окружности» (6 класс) Ещё древние греки находили длину окружности по формуле 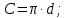 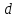 - это диаметр окружности. - это диаметр окружности.Вопрос: а что же такое 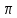 ? ?Работаем в парах, выполняя необходимые измерения. 1.Опоясать стакан ниткой, распрямить нитку, длина нитки примерно равна длине окружности стакана. Чтобы получить более точный результат, нужно это проделать несколько раз. Занесите данные в следующую таблицу.
2.Измерьте диаметр стакана линейкой. Данные занесите в таблицу. 3.Найдите значение 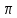 , как неизвестного множителя. Можно пользоваться калькулятором. , как неизвестного множителя. Можно пользоваться калькулятором.4.Каждой паре занести вычисленное значение 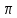 в таблицу на доске. в таблицу на доске.Полученные значения 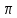
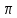 это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой. это бесконечная дробь, современные машины могут определить до миллиона знаков после запятой.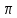 =3,1415926… =3,1415926…Для того, чтобы легче запомнить цифры надо сосчитать количество букв в каждом слове высказывания: «Это я знаю и помню прекрасно» или «Нужно только постараться и запомнить всё как есть: три, четырнадцать, пятнадцать, девяносто два и шесть!» В дальнейшей работе мы будем использовать значение 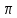 =3,14 =3,14Исследование проведено. На уроке кроме исследовательской работы удачно использовалась работа в парах. Сотрудничество и взаимопомощь принесли желаемый результат. Проблема решена. Приложение 6 Занимательные задачи, используемые на уроках математики в 5 классе №1. Хозяин нанял работника на год и обещал ему дать 12 руб. и кафтан. Но тот, проработав только 7 месяцев, захотел уйти. При расчете он получил кафтан и 5 руб. сколько стоит кафтан? Решение: Не доработал 5 месяцев, не дополучил 7 руб. Значит в месяц 7/5 руб. – 1 р. 40 коп. 7·7/5 = 49/5 = 9 4/5 = 9,8(руб.) (получил бы за 7 мес.) 9,8 – 5 = 4,8 (руб.) стоил кафтан Ответ: 4,8 руб. №2. Из ведра, содержащего 5 литров воды отливают один литр, а затем в ведро вливают 1 литр сока. Перемешав все это, из ведра отливают 1 литр смеси, затем в ведро опять вливают 1 литр сока. Опять перемешивают, отливают 1 литр смеси и вливают 1 литр сока. Сколько в ведре после этого останется воды. Решение: После первого переливания в ведре останется 4 л. Воды отливая 1 л.; смеси - отливаем 1/5 ч. воды, содержащейся в смеси; второе переливание: 4- 1/584 = 3 1/5 = 16/5 л. воды; третье переливание: 16/5 – 1/5 * 16/5 =16/5 – 16/25 = 80/25 – 16/25 = 64/25 (л) воды Ответ: 2 14/25 л. №3. Отец и сын решили перемерить расстояние между двумя деревьями ля чего отошли одновременно от одного и того же дерева. Длина шага отца-70 см., сына 56 см. найти расстояние между деревьями, если известно, что их следы совпали 10 раз. Решение: 70 = 2* 5*7; 56 = 2*7*4 1)НОК(70;56) = 2*5*7*4 = 280(см) – через 280 см следы совпадут 20280*10 = 2800 см = 28 м расстояние между деревьями Ответ: 28 м Приложение 7 Математические ребусы   (Апофема) (Вектор)   (Пять) (Гаусс)     (Дробь) Приложение 8 Памятка для учащихся, решающих проблемные вопросы 1 этап решения проблемы. Осознание проблемы, вскрытие противоречия. На этом этапе необходимо выполнить следующие действия: внимательно прочитать вопрос; найти условие и требование вопроса; определить, что дано в условии и что требуется найти; вспомнить, что вы уже знаете об этом объекте или явлении, какие причинно-следственные связи его объясняют; сопоставить ранее полученные знания и новую информацию; выявить на основании такого сопоставления противоречия, скрытое в вопросе. 2 этап решения проблемы. Формулирование гипотезы. На этом этапе необходимо высказать предположение о причинах возникновения явления или объекта, сформировать гипотезу. 3 этап решения проблемы. Доказательство гипотезы. На этом этапе надо поставить новый вопрос; исходя из предположений, высказанных в гипотезе, ответить на этот вопрос; по возможности проверить этот ответ. этап решения проблемы. Общий вывод. На этом этапе необходимо выполнить следующие действия: ответить на вопросы: 1) какие новые знания вы получили? 2) что вы узнали о причинно-следственных связях, объясняющих это явление или объект? Приложение 9 Решение проблемных ситуаций через организацию учебно-исследовательской деятельности при изучении темы «Дроби» в 5 классе | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
