Филоненко_Радиоизлучение метеорных.... Удк 523. 6 Радиоизлучение метеорных тел в диапазоне декаметровых волн
 Скачать 262.57 Kb. Скачать 262.57 Kb.
|
90 km.
90-100 kм,
750 eV. Это значит, что за время около
-3,3, -4,1, -4,3, -4,7, -6,6 и -7,1. Поэтому можно принять, что средней визуальной светимости
40-60 MHz. На более высоких частотах спектр радиоэмиссии, в соответствии с экспериментом, быстро падает.
2000 Jy на удалении от источника УДК 523.6 РАДИОИЗЛУЧЕНИЕ МЕТЕОРНЫХ ТЕЛ В ДИАПАЗОНЕ ДЕКАМЕТРОВЫХ ВОЛН Филоненко А.Д. (Filonenko A.D) Луганский государственный университет имени Владимира Даля 91034, г. Луганск, квартал Молодежный, 20-А uy5lo@mail.ru 28.02.2017 Аннотация http://www.sciencepublishinggroup.com/journal/comingspecialissues?journalid=122 www.ajmp.org Это «Американский журнал современной физики» Предложена модель процессов, объясняющих собственное радиоизлучение метеорных тел. Для определения некоторых параметров динамики плазменного следа на начальных этапах расширения применена методика решения автомодельной задачи о сильном взрыве. Именно эта стадия расширяющейся плазмы, как показывают расчёты, ответственна за собственное некогерентное и неполяризованное излучение метеороида в верхних слоях атмосферы. В рамках этой модели получена теоретическая оценка величины спектральной плотности потока радиоэмиссии, совпадающая с экспериментальными значениями. Максимум излучения лежит в диапазоне декаметровых волн и сильно зависит от высоты и параметров метеорного тела. Например, при характерных свойствах атмосферы на высоте |
Введение
Давно известно, что прохождение метеорного тела (МТ) через атмосферу Земли сопровождается электрическими явлениями. Характер этих явлений зависит от глубины проникновения и, возможно, имеет разную природу. Достаточно вспомнить такое загадочное явление, как, например, электрофонные болиды [Астапович, 1958], производимый эффект от которых настолько поразителен, что до настоящего времени подвергается сомнению рядом исследователей. Не менее значителна публикация [Obenberger, и др. 1405.6772], в которой сообщается об обнаружении собственного излучения метеоров длинноволновым радиотелескопом LWA1. При обработке массива данных, полученных за 11000 часов для частот между 25 и 75 MHz, было обнаружено 49 радиоимпульсов длительностью от 1 до 10 секунд.
Идентификация радиоисточников на небесной сфере и корреляции с радиоизлучением была проведена на обсерватории All Sky Fireball Network установкой, состоящей из 12 камер кругового обзора, предназначенных для определения 3-х мерного пространственного положения, скорости, абсолютной звёздной величины и массы фаерболла (т.е. светящегося объекта с относительно коротким временем жизни). Установлено кроме этого, что расстояние до объекта излучения не превышает 100 km и что спектральная плотность потока излучения составляет приблизительно
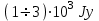 . Результаты этих наблюдений, названы авторами [Obenberger, и др. 1405.6772] нечто новым, которое можно считать информационным прорывом в физике метеорных явлений.
. Результаты этих наблюдений, названы авторами [Obenberger, и др. 1405.6772] нечто новым, которое можно считать информационным прорывом в физике метеорных явлений. В последующих работах авторы [Obenberger, и др. 1405.6772] продолжали набор экспериментальных данных для установления природы излучения метеоров. К моменту публикации [Obenberger, и др. 1503.05150] были проведены дополнительно 2000 часов наблюдений и убедительно доказана метеорная природа радиоэмисии. Были уточнены новые пределы на плотности спектральных потоков и частоту событий. Найдено, что радиовсплески (т.н. транзиенты) длительностью порядка 5 секунд с плотностью энергии > 2,71023, > 1,11023, и > 2,81023 Jm2 Hz1 на частотах 38, 52 и 74 МГц имеют пределы на частоту событий <1,2104, <5,6104 и <7,2104 yr1 deg2. Кроме этого, обработка полученных данных с помощью системы фильтров позволила авторам [Obenberger и др. 1510.04147] проследить динамику спектров и предположить, что радиоэмиссия метеоров может быть следствием возбуждения ленгмюровских волн подобно солнечным радиовсплескам III типа, при которых частотный дрейф наиболее высокий [Железняков, 1958].
Этот впервые проведенный комплекс наблюдений в вышеупомянутых работах и других [Obenberger и др., 1607.03002, 1609.04701] стимулирует выяснение природы излучения метеоров. В настоящей работе использована методика и результаты решения автомодельной задачи о сильном взрыве с цилиндрической симметрией для оценки состояния плазмы на начальных стадиях расширения ионизованного следа метеора. Проведены теоретические оценки интенсивности тормозного излучения с целью проверки её следствий. Ниже представлены результаты теоретического исследования собственного радиоизлучения метеорных тел при взаимодействии их с атмосферой Земли на высоте 90-100 km.
Теоретические оценки спектрального потока радиоизлучения
от ионизованного трека метеорного тела
2.1 Тормозное излучение на стадии «холодной» плазмы
Скорость вторжения метеорного тела в атмосферу Земли составляет, по наблюдениям [Obenberger, и др. 1405.6772] величину порядка
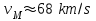 . При такой скорости энергия набегающей молекулы воздуха имеет кинетическую энергию около 750 eV. Взаимодействие потока воздуха с поверхностью метеороида приводит к разогреву и ионизации, как испарившихся молекул метеора, так и молекул воздуха. Ионизованный газ отделяется от метеорного тела и остаётся вдоль его траектории в виде следа, наблюдаемого визуальным, фотографическим или радиолокационным методом. Первостепенным является вопрос о том, какая стадия расширения метеорного следа будет соответствовать максимуму излучения в различных диапазонах длин волн.
. При такой скорости энергия набегающей молекулы воздуха имеет кинетическую энергию около 750 eV. Взаимодействие потока воздуха с поверхностью метеороида приводит к разогреву и ионизации, как испарившихся молекул метеора, так и молекул воздуха. Ионизованный газ отделяется от метеорного тела и остаётся вдоль его траектории в виде следа, наблюдаемого визуальным, фотографическим или радиолокационным методом. Первостепенным является вопрос о том, какая стадия расширения метеорного следа будет соответствовать максимуму излучения в различных диапазонах длин волн. Плазменный след испарившихся атомов вещества через время порядка одной миллисекунды достигают т.н. начального радиуса
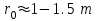 . Теория начального радиуса разрабатывалась многими авторами и сейчас согласно физической теории метеоров, считается, что к этому моменту расширения вследствие столкновений с молекулами атмосферы температура всех частиц становиться равной температуре окружающей среды. Разреженная атмосфера на высоте 90-100 km сильно затрудняет рекомбинацию и «прилипание» электронов к молекулам кислорода. Поэтому при дальнейшем расширении линейная плотность электронов в следе метеора остаётся постоянной.
. Теория начального радиуса разрабатывалась многими авторами и сейчас согласно физической теории метеоров, считается, что к этому моменту расширения вследствие столкновений с молекулами атмосферы температура всех частиц становиться равной температуре окружающей среды. Разреженная атмосфера на высоте 90-100 km сильно затрудняет рекомбинацию и «прилипание» электронов к молекулам кислорода. Поэтому при дальнейшем расширении линейная плотность электронов в следе метеора остаётся постоянной. Тормозное радиоизлучение в этом случае вызвано столкновениями электронов с нейтральными молекулами, атомами или ионами в ионизированном следе метеора. Подобное явление имеет сходство с излучением широкого атмосферного ливня т.н. ионизационными электронами, т.е. электронами, у которых энергия недостаточна для ионизации нейтральных молекул атмосферы [Филоненко, 2014, 2015]. Прохождение ливня через атмосферу вызывает возбуждение молекул или их ионизацию. В целом процесс распространения ливня сопровождается оптическим свечением и радиоизлучением. Разумеется, это только внешнее сходство с фаерболлом. Физическая природа этих явлений различна.
В рассматриваемом случае спектральная мощность тормозного излучения зависит от количества электронов, участвующих одновременно в процессе излучения, средней скорости электронов
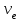 и коэффициента поглощения ионизованного газа. В частности, при отсутствии поглощения в плазме дифференциальная мощность излучения одного электрона выражается известной формулой [Бекефи, 1971]:
и коэффициента поглощения ионизованного газа. В частности, при отсутствии поглощения в плазме дифференциальная мощность излучения одного электрона выражается известной формулой [Бекефи, 1971]: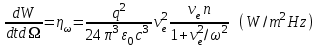 (1)
(1)где
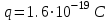 заряд электрона,
заряд электрона, 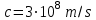 скорость света в вакууме,
скорость света в вакууме, 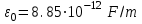 электрическая постоянная, n показатель преломления плазмы,
электрическая постоянная, n показатель преломления плазмы, 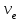 среднее число столкновений электрона с атомами или ионами в единицу времени, частота излучения.
среднее число столкновений электрона с атомами или ионами в единицу времени, частота излучения.Согласно эмпирическим данным и теоретическим оценкам величина линейной плотности электронов в следе зависит от массы и скорости метеорного тела [Кащеев и др, 1967, Белькович, 1971]:
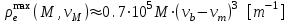
где, M масса метеора,
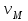 скорость метеора,
скорость метеора, 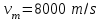 . Оптические измерения [Obenberger, и др. 1405.6772] показывают, что четыре видимых МТ (в радиоканале 38 MHz) имели пик абсолютной визуальной величины М*
. Оптические измерения [Obenberger, и др. 1405.6772] показывают, что четыре видимых МТ (в радиоканале 38 MHz) имели пик абсолютной визуальной величины М* 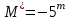 соответствует масса метеора порядка
соответствует масса метеора порядка 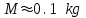
 [Кащеев и др, 1967; Белькович, 1971; Бронштэн, 1981; Мартынов, 1988; Бабаджанов, 1987].
[Кащеев и др, 1967; Белькович, 1971; Бронштэн, 1981; Мартынов, 1988; Бабаджанов, 1987].Для самой высокой скорости метеора с массой
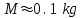 линейная плотность электронов составит величину порядка
линейная плотность электронов составит величину порядка 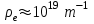 . За время равное приблизительно
. За время равное приблизительно 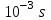 след в виде цилиндра достигнет радиуса
след в виде цилиндра достигнет радиуса 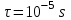 вблизи оси метрового отрезка (
вблизи оси метрового отрезка (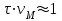 ) траектории выделяется энергия приблизительно на 4 порядка большая, чем внутренняя энергия невозмущённой области атмосферы в этом объёме.
) траектории выделяется энергия приблизительно на 4 порядка большая, чем внутренняя энергия невозмущённой области атмосферы в этом объёме. Этот факт свидетельствуют о том, что для определения параметров состояния газа в возмущённой области могут быть использованы результаты решения автомодельной задачи о сильном взрыве [Седов, 1977]. В момент отрыва молекул от испаряющегося МТ их скорость направлена практически вдоль линии движения. Перпендикулярная составляющая скорости по величине близка к тепловой. Поэтому область возмущённой атмосферы вместе с молекулами МТ в начальный момент времени будет представлять собой цилиндр с диаметром близким по величине к характерному размеру метеороида. Учитывая это, можно считать, что под действием начального высокого давления от области энерговыделения в невозмущённой атмосфере начинает распространяться цилиндрическая ударная волна (УВ).
2.2 Модель цилиндрической ударной волны и тормозное излучение
«горячей» плазмы
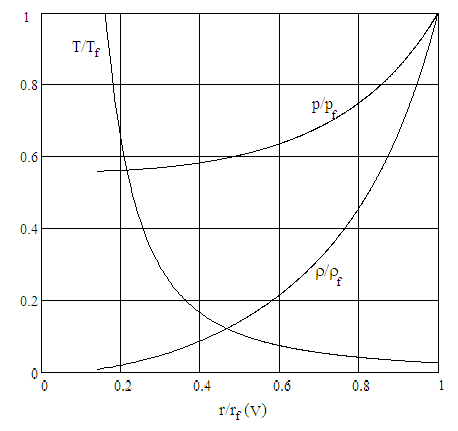
Распределение давления, плотности и радиальной скорости газа (p,,u) в области за УВ зависит от одной автомодельной переменной, которая пропорциональна безразмерной комбинации
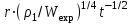 (для цилиндрической симметрии). Здесь
(для цилиндрической симметрии). Здесь 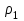 плотность невозмущённой атмосферы,
плотность невозмущённой атмосферы, 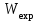 энергия взрыва, т.е. кинетическая энергия молекул испаряющегося МТ, t текущее время, r кратчайшее расстояние от произвольной точки цилиндра до его оси. Решение задачи о сильном взрыве найдено Л.И. Седовым в виде функций
энергия взрыва, т.е. кинетическая энергия молекул испаряющегося МТ, t текущее время, r кратчайшее расстояние от произвольной точки цилиндра до его оси. Решение задачи о сильном взрыве найдено Л.И. Седовым в виде функций 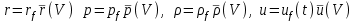 , где индексом f обозначены величины давления, плотности и скорости на фронте УВ, зависящие от времени,
, где индексом f обозначены величины давления, плотности и скорости на фронте УВ, зависящие от времени, 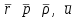 безразмерные функции безразмерного параметра V, величина которого в случае цилиндрической симметрии для показателя =1.3 изменяется в пределах 0.385<V<0.435. В этой области величина отношения
безразмерные функции безразмерного параметра V, величина которого в случае цилиндрической симметрии для показателя =1.3 изменяется в пределах 0.385<V<0.435. В этой области величина отношения 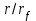 изменяется в пределах
изменяется в пределах 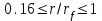 [Седов, 1977].
[Седов, 1977]. Сильный взрыв в воздухе сопровождается высокими температурами и во взрывной волне идут процессы диссоциации и ионизации молекул, которые уменьшают эффективный показатель адиабаты по сравнению со значением =7/5, соответствующим холодной атмосфере. Это связано с тем, что в результате ионизации атомов возрастает количество свободных электронов и разность
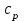 и
и 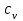 возрастает. Поэтому предпочтительное значение выбирается в пределах 1.2<<1.3 [Седов, 1977; Райзер, 2011]. Далее везде принято значение =1.3.
возрастает. Поэтому предпочтительное значение выбирается в пределах 1.2<<1.3 [Седов, 1977; Райзер, 2011]. Далее везде принято значение =1.3. С учётом этих замечаний решение [Седов, 1977] для цилиндрического взрыва можно кратко записать, как
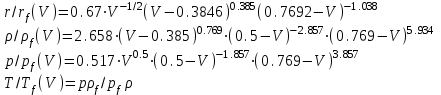 (2)
(2)Соответствующие величины на фронте цилиндрической УВ в зависимости от текущего момента времени и радиуса
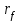 выражаются следующими формулами:
выражаются следующими формулами: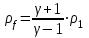 ,
, 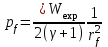 ,
, 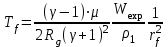 , (3)
, (3)где
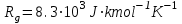 газовая постоянная, молярная масса и
газовая постоянная, молярная масса и 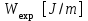 энергия взрыва, приходящаяся на единицу длины цилиндра. В начале расширения УВ вещество за фронтом будет представлять собой смесь электронов и атомов (ионов) атмосферы, поэтому молярная масса будет значительно меньше, чем для невозмущённой атмосферы =29 g/mol. Далее принято приблизительное значение =14 g/mol. В выражениях (3) давление и температура при
энергия взрыва, приходящаяся на единицу длины цилиндра. В начале расширения УВ вещество за фронтом будет представлять собой смесь электронов и атомов (ионов) атмосферы, поэтому молярная масса будет значительно меньше, чем для невозмущённой атмосферы =29 g/mol. Далее принято приблизительное значение =14 g/mol. В выражениях (3) давление и температура при 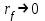 стремятся к бесконечности, что является результатом идеализации задачи о сильном взрыве. Практически, решение этой задачи можно использовать для значений такого радиуса фронта
стремятся к бесконечности, что является результатом идеализации задачи о сильном взрыве. Практически, решение этой задачи можно использовать для значений такого радиуса фронта 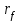 , при котором начальная масса всех молекул метеора
, при котором начальная масса всех молекул метеора 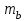 будет меньше массы атмосферы в объёме этого цилиндра [18], т.е. когда
будет меньше массы атмосферы в объёме этого цилиндра [18], т.е. когда 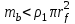 , где
, где 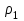 плотность невозмущённой атмосферы. Например, такое соотношение наступает при значениях
плотность невозмущённой атмосферы. Например, такое соотношение наступает при значениях 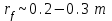 для массы метеороида порядка M
для массы метеороида порядка M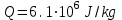 теплота испарения железа,
теплота испарения железа, 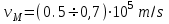 скорость МТ, S площадь поперечного сечения МТ, плотность МТ. Молекулы испаряющегося метеороида вследствие рассеяния и диффузии попадают в неподвижную атмосферу, и кинетическая энергия удельной массы dM/dx является начальной энергией
скорость МТ, S площадь поперечного сечения МТ, плотность МТ. Молекулы испаряющегося метеороида вследствие рассеяния и диффузии попадают в неподвижную атмосферу, и кинетическая энергия удельной массы dM/dx является начальной энергией 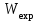 взрыва для цилиндра единичной длины. Допуская, что форма метеороида близка к сферической, получим
взрыва для цилиндра единичной длины. Допуская, что форма метеороида близка к сферической, получим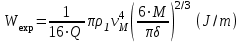 . (15)
. (15)Подставляя характерные данные в выражение (9) для диэлектрической проницаемость плазмы, легко убедиться, что проницаемость в зависимости от частоты для некоторого интервала значений x<1 может быть отрицательной. Как известно, в плазме с отрицательной проницаемостью электромагнитные волны не распространяются свободно, а испытывают сильное затухание. Вследствие этого следует ожидать, что излучение будет эффективным только в относительно тонком слое плазмы, близком к фронту УВ, т.е. в таком слое, где температура будет ещё достаточно высока, а поглощение в этой области не слишком велико. Другими словами, существует значение переменной
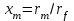 (для заданного
(для заданного 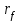 ), при котором спектральная плотность потока будет максимальна.
), при котором спектральная плотность потока будет максимальна. 2.2.1 Спектральная плотность потока излучения
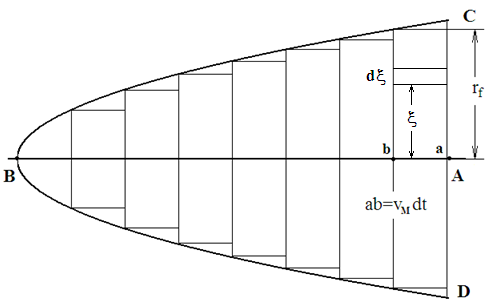
Выражение (1) даёт спектральную мощность излучения одного электрона в ионизованном газе. Чтобы получить полную мощность, нужно учесть все электроны, излучающие одновременно в процессе движения метеорного тела. Для этого определим пространственную конфигурацию плазмы, сопровождающей движение и излучение метеороида. Заметим, что нахождение метеорного тела в некоторой точке пространства соответствует зарождению УВ. Пусть точка А (рис.2) соответствует месту нахождения метеора и зарождению УВ в некоторый момент времени t. Через интервал равный
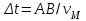 , метеор будет находиться в точке В, а фронт УВ в точке А за это время достигнет радиуса
, метеор будет находиться в точке В, а фронт УВ в точке А за это время достигнет радиуса 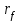 . Для достижения такого радиуса необходимо время равное [Седов, 1977]
. Для достижения такого радиуса необходимо время равное [Седов, 1977] 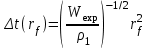 .
. Все электроны, находящиеся в пространстве под фигурой вращения степенной функции
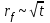 , излучают одновременно. Другими словами, пока МТ перемещалось вдоль отрезка АВ, элементарный цилиндр с высотой
, излучают одновременно. Другими словами, пока МТ перемещалось вдоль отрезка АВ, элементарный цилиндр с высотой 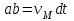 радиально расширился до величины
радиально расширился до величины 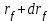 и всё это время излучал. Однако, как показывают дальнейшие расчёты, вследствие сильного поглощения, излучала только его часть, очень близкая к фронту УВ. Для нахождения полной мощности излучения необходимо сложить мощность излучения всех элементарных цилиндров.
и всё это время излучал. Однако, как показывают дальнейшие расчёты, вследствие сильного поглощения, излучала только его часть, очень близкая к фронту УВ. Для нахождения полной мощности излучения необходимо сложить мощность излучения всех элементарных цилиндров.Мощность излучения в момент времени t одного такого произвольного цилиндра с высотой
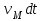 , когда радиус фронта равен
, когда радиус фронта равен 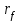 , будет:
, будет: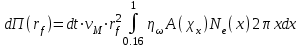 , (16)
, (16)где
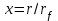 , а пределы интегрирования соответствуют пределам параметра V, т.е. 0.385<V<0.435 (см. выше). Для наблюдателя, находящегося на расстоянии R от метеороида, полный спектральный поток излучения равен интегралу от выражения (16) по элементам времени
, а пределы интегрирования соответствуют пределам параметра V, т.е. 0.385<V<0.435 (см. выше). Для наблюдателя, находящегося на расстоянии R от метеороида, полный спектральный поток излучения равен интегралу от выражения (16) по элементам времени 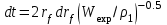 :
: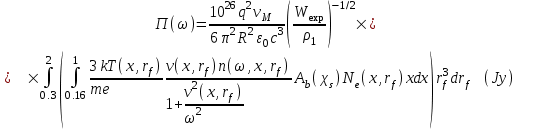 . (17)
. (17)Здесь выбор нижнего предела интегрирования по переменной
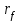 обсуждался выше, а верхний предел
обсуждался выше, а верхний предел 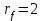 соответствует тому факту, что для радиуса
соответствует тому факту, что для радиуса 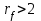 излучением можно пренебречь (см. (16)).
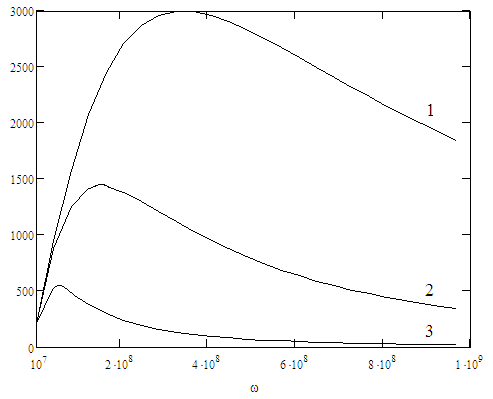
излучением можно пренебречь (см. (16)). На рис.3 представлены энергетические спектры (17) излучения МТ для трёх различных высот 90 km, 95 km, и 100 km. Максимумы спектров приходятся на частоты
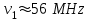 ,
,  ,
, 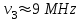 ,
, Очевидно, что плотность спектрального потока сильно зависит от высоты. Графики получены для характерных значений и физических констант:
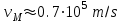 ,
, 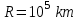
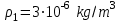 (для высоты h=90km),
(для высоты h=90km), 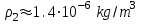 (h=95 km),
(h=95 km), 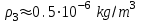 (h=100 km),
(h=100 km), 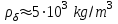 плотность метеороида, =0.05 kg масса метеороида.
плотность метеороида, =0.05 kg масса метеороида. Выводы
Вследствие подобия плазменного следа метеора расширяющемуся объекту с высокой плотностью энергии, для определения параметров плазмы был выбран метод решения автомодельной задачи о сильном взрыве с цилиндрической симметрией. В приведенные выше расчёты спектральной плотности потока излучения метеороида нетрудно ввести зависимость ряда величин от текущей высоты и угла наклона траектории. Однако такое уточнение решения вряд ли целесообразно на первом этапе исследования. Полученное здесь решение задачи о радиоизлучении отвечает на принципиальный вопрос о том, возможно ли такое явлений хотя бы при каких-то особых условиях, реализующихся при прохождении метеороида через атмосферу Земли.
Как известно, постановка задачи об УВ сильно идеализирована и предполагает, что в начальный момент давление на оси цилиндра нулевого радиуса равно нулю, а затем мгновенно выделяется энергия, в результате чего по атмосфере распространяется цилиндрическая ударная волна. Несмотря на такие крайне экстремальные начальные условия, наука имеет немало примеров применений решения к реальным объектам, которые дали хорошее согласие с экспериментом.
Автомодельная задача также предполагает, что её решение справедливо до такой стадии расширения УВ, при которой давление за фронтом остаётся всё ещё на порядки большим, чем перед фронтом УВ. Легко убедиться, что в используемой модели метеора это условие выполняется, т.е.
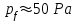 для
для 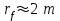 а атмосферное давление
а атмосферное давление 
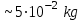 спектральный поток составляет
спектральный поток составляет 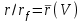 и
и 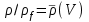 , а функции
, а функции 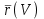 и
и 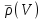 известны (см. (2)), то можно отношение
известны (см. (2)), то можно отношение 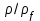 выразить через относительный радиус
выразить через относительный радиус 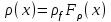 . Аналогично для давления
. Аналогично для давления 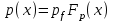 и температуры
и температуры 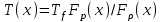 .
.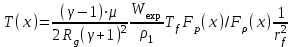 (4)
(4)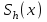 для вычисления концентрации электронов
для вычисления концентрации электронов 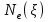 в зависимости от температуры Т=Т(x):
в зависимости от температуры Т=Т(x):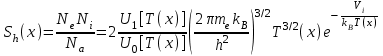 (5)
(5)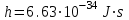 постоянная Планка,
постоянная Планка, 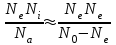 . Здесь
. Здесь 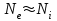 концентрация ионов и электронов,
концентрация ионов и электронов, 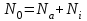 полное число всех атомов,
полное число всех атомов, 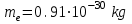 масса электрона,
масса электрона, 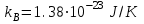 постоянная Больцмана,
постоянная Больцмана, 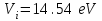 потенциал ионизации атома азота. При вычислении степени ионизации допущено, что атмосфера состоит преимущественно из молекул азота, но поскольку энергия диссоциации азота (9.76 eV) намного меньше энергии ионизации, то даже при относительно низкой температуре молекулы распадаются гораздо раньше, чем наступает ионизация атомов. Функции
потенциал ионизации атома азота. При вычислении степени ионизации допущено, что атмосфера состоит преимущественно из молекул азота, но поскольку энергия диссоциации азота (9.76 eV) намного меньше энергии ионизации, то даже при относительно низкой температуре молекулы распадаются гораздо раньше, чем наступает ионизация атомов. Функции 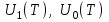 статистические суммы, соответствующие первой ступени ионизации. Для не очень «горячей» плазмы их отношение близко к единице. Такой факт имеет место непосредственно за фронтом УВ, где температура наименьшая, а интенсивность излучения (как будет видно далее) наибольшая. От более глубоких слоёв плазмы излучение за пределы границы фронта УВ не выходит вследствие сильного поглощения.
статистические суммы, соответствующие первой ступени ионизации. Для не очень «горячей» плазмы их отношение близко к единице. Такой факт имеет место непосредственно за фронтом УВ, где температура наименьшая, а интенсивность излучения (как будет видно далее) наибольшая. От более глубоких слоёв плазмы излучение за пределы границы фронта УВ не выходит вследствие сильного поглощения. 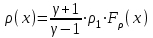 (6)
(6)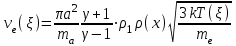 , (7)
, (7)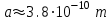 эффективный диаметр атома азота при столкновении с электронами.
эффективный диаметр атома азота при столкновении с электронами.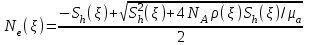 , (8)
, (8) 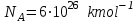 число Авогадро.
число Авогадро. 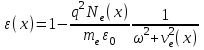 , (9)
, (9)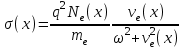 (10)
(10) 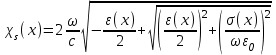 . (11)
. (11)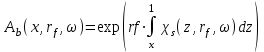 (12)
(12)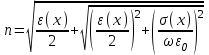 (13)
(13) 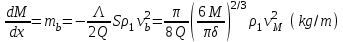 (14)
(14)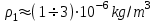 плотность атмосферы на высоте
плотность атмосферы на высоте 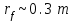 . Во-вторых, решение показывает, что интенсивно излучающий слой толщиной несколько миллиметров находится на поверхности цилиндра. С другой стороны, известно, что толщина поверхности разрыва не может быть менее одного свободного пробега молекулы. А на высоте порядка 95 km свободный пробег составляет несколько сантиметров. Учёт этого факта сильно бы осложнил расчёт излучения и поглощения радиоволн. Поэтому в простейшем варианте (для плоского случая) было проверено изменение интенсивности излучения (с учётом поглощения) в зависимости от толщины излучающего слоя d, в котором полное число электронов
. Во-вторых, решение показывает, что интенсивно излучающий слой толщиной несколько миллиметров находится на поверхности цилиндра. С другой стороны, известно, что толщина поверхности разрыва не может быть менее одного свободного пробега молекулы. А на высоте порядка 95 km свободный пробег составляет несколько сантиметров. Учёт этого факта сильно бы осложнил расчёт излучения и поглощения радиоволн. Поэтому в простейшем варианте (для плоского случая) было проверено изменение интенсивности излучения (с учётом поглощения) в зависимости от толщины излучающего слоя d, в котором полное число электронов 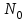 постоянно, а концентрация изменяется, как отношение
постоянно, а концентрация изменяется, как отношение 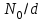 . В этом случае размытая граница раздела не внесла существенных изменения в интенсивность излучения.
. В этом случае размытая граница раздела не внесла существенных изменения в интенсивность излучения. 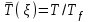 , давления
, давления 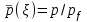 и плотности
и плотности 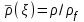 от безразмерного радиуса
от безразмерного радиуса 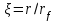 . Индекс f соответствует значениям параметров плазмы на фронте УВ. V безразмерный параметр, величина которого изменяется в пределах 0.385
. Индекс f соответствует значениям параметров плазмы на фронте УВ. V безразмерный параметр, величина которого изменяется в пределах 0.385