ПОГРЕШНОСТЬ. Погрешности_измерений_Обработка_результатов_эксперимента_Н_Н_Сми. Уметь пользоваться современной научной аппаратурой для проведения инженерных измерений и научных исследований использовать основные приемы обработки экспериментальных данных владеть

• Название: Уметь пользоваться современной научной аппаратурой для проведения инженерных измерений и научных исследований использовать основные приемы обработки экспериментальных данных владеть
• Анкор: ПОГРЕШНОСТЬ
• Дата: 13.04.2023
• Размер: 2.72 Mb.
• Имя файла: Погрешности_измерений_Обработка_результатов_эксперимента_Н_Н_Сми.doc
• Тип: Практикум; #1060244

Введение

Цель проведения лабораторного практикума, как и преподавания дисциплины в целом - обеспечить приобретение знаний и умений по физике в соответствии с Федеральным государственным образовательным стандартом (ФГОС) по различным направлениям подготовки специалистов.

В соответствии с требованиями ФГОС к результатам освоения дисциплины лабораторный практикум направлен на формирование общих и профессиональных компетенций, заключающихся в способностях:

• 
  организовать свою работу ради достижения поставленных целей;
  
• 
  применять на практике навыки проведения и описания исследований, в том числе экспериментальных;
  
• 
  работать самостоятельно;
  
• 
  использовать инновационные идеи;
  
• 
  принимать участие в научно-исследовательских разработках по профилю подготовки: систематизировать информацию по теме исследований, принимать участие в экспериментах, обрабатывать полученные данные.
  

Задачилабораторного практикума:

• 
  ознакомление с современной научной аппаратурой;
  
• 
  формирование навыков проведения физического эксперимента;
  
• 
  формирование навыков умения оценить степень достоверности результатов, полученных в процессе экспериментального исследования;
  
• 
  овладение методами физического исследования и оценки степени достоверности полученных результатов.
  

В результате выполнения физического лабораторного практикума студент должен:

уметь пользоваться современной научной аппаратурой для проведения инженерных измерений и научных исследований; использовать основные приемы обработки экспериментальных данных; владеть методамиэкспериментальногоисследования в физике, которые включают планирование, постановку и обработку результатов эксперимента (компьютерную, аналитическую, графическую).

ЭКСПЕРИМЕНТ И ИЗМЕРЕНИЯ

Эксперимент ‑ (от латинского experimentum – проба, опыт) – это метод познания, при помощи которого в контролируемых и управляемых условиях исследуются явления действительности. Эксперимент можно определить как систему операций и планомерно проведенных наблюдений, направленных на получение информации об объекте.

Число признаков, которые используются для классификации экспериментов, достаточно велико. Эксперименты различаются:

по способу формирования условий (естественные, искусственные);

по целям исследования (преобразующие, констатирующие, контролирующие, поисковые, решающие);

по организации проведения (лабораторные, натурные, полевые, производственные);

по числу варьируемых факторов (однофакторный и многофакторный) и так далее по многим другим признакам.

Для современного горного производства залогом его успешного развития является высокий уровень информационного обеспечения экспериментального характера.

Основным источником измерительной информации, без которой невозможен прогресс в науке и технике, является научная и производственная экспериментальная деятельность.

С основами измерений студенты сталкиваются в течение всего срока обучения при проведении лабораторных работ по различным дисциплинам.

Измерить – сравнить с эталоном, найти отношение к величине того же вида принятой за единицу.

Измерение – нахождение значений физической величины экспериментальным путем с помощью специальных измерительных средств.

Классификация измерений по некоторым классификационным признакам приведена в таблице 1.
Таблица 1.

Классификация измерений

Классификационный признак	Наименование измерений
Характеристика точности	равноточные
	неравноточные
Число измерений в серии	однократные
	многократные
Выражение результата измерений	абсолютные
	относительные
Общие приемы получения результатов измерений	прямые
	косвенные
	совокупные
	совместные
Метрологическое назначение	технические
	исследовательские
	метрологические
Характер зависимости измеряемой величины от времени измерения	статические
	динамические

Измерение любой величины не дает абсолютно точного значения этой величины. Каждое измерение всегда содержит некоторую погрешность (ошибку). Задача физического эксперимента состоит не только в получении искомой величины, но и в оценке того, с какой точностью эта величина измерена. Этой цели служит теория погрешности.

Следует отличать характеристику результата измерения от метрологической характеристики средства измерения.

Погрешность результата измерения - отклонение измеренного значения физической величины от её истинного значения.

Погрешность средств измерения – количественное выражение отклонения номинального значения физической величины, воспроизводимой или измеряемой данным средством измерения, от её истинного значения.

В таблице 2 представлена классификация погрешностей измерений и средств измерений по наиболее существенным признакам.

Таблица 2.

Классификация погрешностей измерений и средств измерений

Классификационный признак	Погрешности
	измерений	средств измерений
Источники возникновения	Методическая	-
	Инструментальная
	Субъективная
Характер проявления	Систематическая
	Случайная
	Грубая
Способ выражения	Абсолютная
	Относительная
		Приведенная
Условия изменения измеряемой величины	Статическая
	Динамическая
Способ обработки ряда изменений	Средняя арифметическая	-
	Средняя квадратичная
Полнота охвата измерительной задачи при косвенных измерениях	Частная	-
	Полная
Условия применения средств измерения		Основная
		Дополнительная
Зависимость погрешности от значения измеряемой величины		Аддитивная
		Мультипликативная

Оценка погрешностей, допущенных при измерениях, и оценка достоверности полученных результатов выполняется в ходе обработки экспериментальных данных.

ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В ФИЗИЧЕСКОМ ЭКСПЕРИМЕНТЕ

Цель обработки результатов ‑ оценить полученный цифровой материал и привести его в удобные формы представления, которые позволяют быстро и качественно сопоставлять, и анализировать различные результаты.

1. Формы и методы обработки результатов измерений

Важнейшим этапом программы эксперимента является выбор методов обработки и анализа экспериментальных данных.

Формами представления экспериментального материала могут служить таблицы, графики, номограммы, формулы.

Таблица, как правило, используется для записи результатов непосредственных измерений и результатов расчета параметров, если не используется автоматическая обработка данных с применением компьютера.

Основные методы обработки экспериментальных данных: графические, математические, критериальные и их сочетания.

Графические методы используются для наиболее наглядного представления экспериментальных результатов, понимания их физической сущности, выявления тенденции и общего характера функциональной связи между величинами, наглядного определения экстремума. Как правило, графические методы предшествуют обработке данных с помощью математического аппарата. При необходимости выполнять расчеты по полученным эмпирическим формулам от многих переменных рационально построение номограмм, завершающих процесс математической обработки данных.

Для графического изображения экспериментальных результатов, как правило, применяют систему прямоугольных координат.

Для более наглядного изображения нелинейных функций применяют полулогарифмические и логарифмические координаты сетки.

Для изображения экстремумов функций необходимо использовать более плотную информацию об измеряемой величине.

Математические методы обработки и анализа данных применяются для оценок погрешностей и достоверностей установления критериев, доверительных интервалов, тесноты связей, эмпирических формул и т.д.

Критериальные методы обработки используют для получения оценки, распространяющейся не только на один полученный результат, но и на целый класс явлений. Обобщенная критериальная зависимость незаменима при изучении сложных систем при большом количестве варьируемых факторов. Критериальная обработка результатов позволяет сократить количество варьируемых факторов за счет их комбинаций в критерии подобия и тем самым уменьшить число необходимых экспериментов.

2. Аппроксимация экспериментальных данных

Важнейшей задачей физического эксперимента является установление функциональной зависимости между изучаемыми признаками, например, двумя переменными физическими величинами.

Графическое изображение точек на плоскости, конечно, позволяет наглядно представить динамику развития процесса, выявить определенные тенденции, но для обеспечения удобства последующего практическое использование полученных эмпирических результатов в вычислениях, математических моделях, задачах оптимизации и во многих других случаях необходимо решение ряда проблем.

Как правило, возникает необходимость интерполировать, или экстраполировать функциональную зависимость, т.е. найти значения функции соответствующие аргументу, лежащие внутри или вне области эксперимента. Имеющиеся погрешности эксперимента в значениях полученных величин желательно «сгладить». Это приводит к задаче построения аппроксимирующей (приближающей) функции, описывающей зависимость между величинами, полученными в результате экспериментальных измерений. Формулы, изображающие такую функциональную зависимость, называются эмпирическими формулами.

Процесс построения аппроксимирующей функции состоит из двух этапов:

- выяснение общего вида приближающей функции;

- определение параметров, для которых приближение оказывается наилучшим.

В учебном физическом эксперименте, как правило, одной из задач является сопоставление полученных экспериментальных данных с теоретическими зависимостями, лежащими в основе лабораторной работы. Выбор аппроксимирующей функции определён законами (соотношениями), определяющими физические величины формулами из соответствующего раздела физики и однозначно определяет вид приближающей функции.

В случае лабораторной работы с элементами научно – исследовательского характера вид аппроксимирующей функции может быть произвольным.

Поэтому сначала полученные опытные точки наносятся на график и оцениваются визуально. Затем подбирается соответствующего вида кривая, желательно из числа наиболее простых элементарных функций с минимальным числом параметров.

После соответствующего выбора вида функции переходят к этапу определения параметров приближающей функции уже заданного вида одним из математических методов.

Основным принципом, при этом является необходимость прохождения кривой между измеренными точками так, чтобы некоторая заданная мера для отклонения оказалась минимальной. Эта задача является основной задачей выравнивания (сглаживания) результатов измерения и вывода эмпирических формул.

Существуют различные математические методы решения задачи аппроксимации. Наибольшее распространение получил метод наименьших квадратов, разработанный Гауссом. Его краткое изложение представлено в приложении 1. В компьютерной программе ЕХЕL реализация метода осуществляется при использовании режима линии тренда и выбранного закона аппроксимации экспериментальных данных.

3. Оценка погрешностей измерений

Вычисление случайных погрешностей при прямых измерениях

При прямых измерениях значение искомой величины получают непосредственно по показаниям измерительного прибора. Так, например, длина измеряется линейкой, время по часам и т. д.

При проведении измерений величины х, из-за наличия случайных ошибок, получаем n различных значений: х₁, х₂, х₃… х_n

Истинным значением некоторой величины х принято считать среднее арифметическое значение этой величины.

,

.

Разность между средним значением и результатом i – го измерения называют абсолютной погрешностью отдельного измерения величины х



Средняя абсолютная погрешность измерения величины х

.

Для характеристики точности измерений служит относительная ошибка, которую принято выражать в процентах или в частях целого

ּ .

Доверительный интервал – интервал значений величины х, внутри которого с определенной вероятностью, называемой доверительной, находится величина х_ист:

.

Для нахождения доверительного интервала и доверительной вероятности необходимо установить закон, которому подчиняются случайные отклонения измеряемой величины от ее среднего арифметического значения. Этот закон – функция распределения, или плотность вероятности величины х.

.

Зная , можно определить вероятность того, что непрерывная случайная величина будет иметь значение в интервале от до .

.
Кривая нормального распределения и ее физический смысл

В 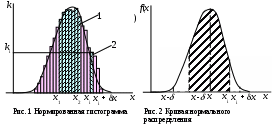лабораторном эксперименте проведено n измерений одной и той же физической величины и получены ее значения х₁, х₂, х₃,...х_n. Отложив эти значения в виде точек на оси абсцисс (рис.1), получим на этой оси множество точек (если число измерений достаточно велико), причем их плотность в одних местах будет больше, в других меньше. Выделим на оси абсцисс равные интервалы Δx = , и сосчитаем, сколько точек попало в каждый интервал. Построив над каждым интервалом прямоугольник с высотой, равной количеству точек в данном интервале, получим ступенчатую кривую (гистограмму).

Например, в выделенный интервал, заключенный между значениями х_i и х_i + , попало k_i точек и высота прямоугольника 1 равна k_i.

Отношение площади выделенного прямоугольника к площади всех прямоугольников, т.е. k_i/[(k₁ + k₂+ ... + k_n)] = k_i/n = k_i/n, определяет вероятность того, что при проведении единичного измерения его результат окажется в интервале между х_i и x_i + .

Гистограмму строят так, чтобы сумма площадей всех прямоугольников была равна единице (такая процедура называется нормировкой). Тогда вероятность попадания результата измерения в интервале от х₁ до х₂ равна суммарной площади прямоугольников, заключенных между х₁ и х₂.

Если неограниченно увеличивать число измерений n, а интервал  устремить к нулю, то в пределе нормированная гистограмма перейдет в непрерывную кривую (рис.2), которую называют кривой нормального распределения. Функция распределения определяется формулой Гаусса



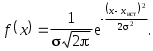
Физический смысл остается тем же: площадь под любым участком кривой нормального распределения равна вероятности «попадания» результата измерения в интервал х, ограниченный этим участком.

Входящую в формулу Гаусса величину  называют стандартным отклонением, а ² - дисперсией измерения.

При достаточно большом числе измерений стандартное отклонение (или средняя квадратичная ошибка) определяется по формуле



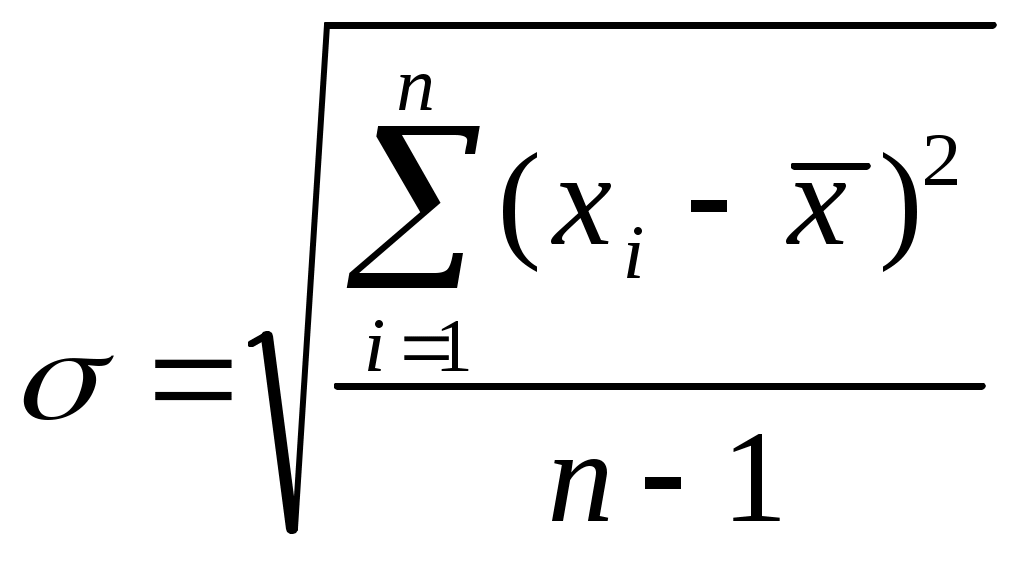
Средняя квадратичная ошибка  используется, когда необходимо знать надежность полученных результатов.

В случае выполнения серии измерений, необходимо рассчитать средние арифметические каждого отдельного измерения и их средние квадратичные погрешности , а затем определить среднюю квадратичную погрешность серии независимых прямых измерений одной и той же величины по формуле



или средняя квадратичная ошибка среднего значения



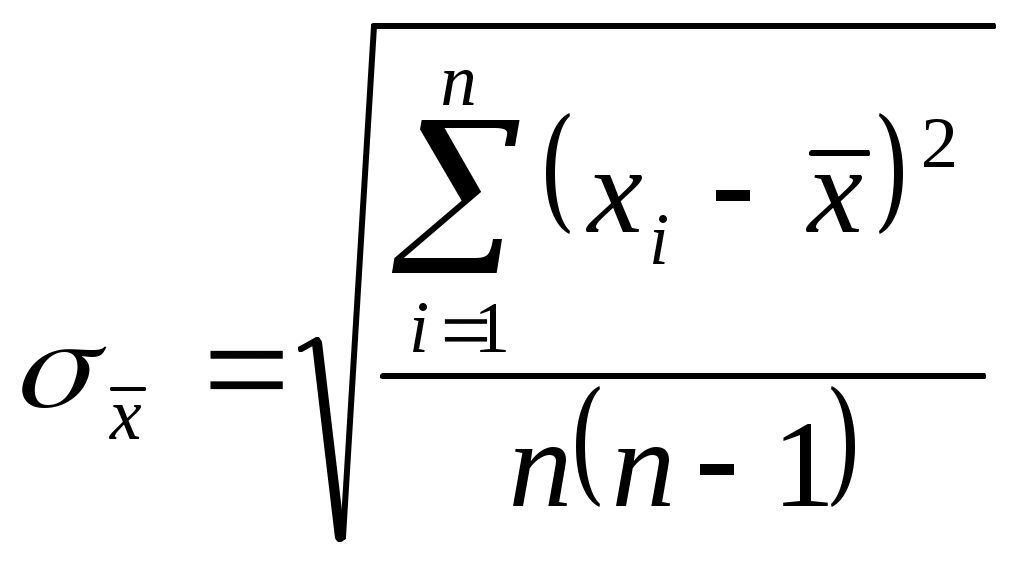
где:  - средняя квадратичная ошибка каждого отдельного измерения, n – число измерений.

При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем).

Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки.

Физический смысл средней квадратичной погрешности.
При любых численных значениях стандартного отклонения для доверительного интервала (рис.2) доверительная вероятность всегда равна 0,68. То есть можно утверждать, что с вероятностью 68 % результат единичного измерения окажется в интервале от до или, что то же самое, с вероятностью 68 % ошибка единичного измерения не превышает величины стандартного отклонения (среднеквадратичной погрешности).

Доверительному интервалу от до соответствует доверительная вероятность 95 %, а доверительному интервалу от до - доверительная вероятность 99,7 %.

Если ограничится доверительной вероятностью 68 %, то величину стандартного отклонения  используют для оценки случайной погрешности. При этом результат измерений величины х должен быть представлен в виде Эта запись означает, что с вероятностью 68 % результат единичного измерения величины х окажется в интервале значений от ( ) до ( ).
Учет систематических ошибок
Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.

Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. У неэлектрических приборов, имеющих шкалу с делениями, принимают в качестве систематической ошибки половину цены деления прибора. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм. Приборы, имеющие дополнительную шкалу (нониус), имеют точность измерений, соответствующую дополнительной шкале. Например, для измерений штангенциркулем – 0,1–0,05 мм; микрометром – 0,01 мм.

На шкалах электроизмерительных приборов указывается класс точности. Согласно ГОСТу, электроизмерительные приборы делятся по степени точности на семь классов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆х по формуле



где К – класс точности прибора в процентах, x_пр – предельное значение величины, которое может быть измерено по шкале прибора.

Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более



Среднее значение полной погрешности складывается из случайной и систематической погрешности



Ответ с учетом систематических и случайных ошибок записывается в виде


Погрешность косвенного измерения
Если искомая физическая величина не может быть измерена непосредственно прибором, а посредством формулы выражается через измеряемые величины, то такие измерения называются косвенными.

Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку косвенных измерений.

Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.

Пусть физическая величина (x, y, z, ...) является функцией ряда независимых аргументов x, y, z, ..., каждый из которых может быть определен экспериментально. Путем прямых измерений определяются величины и оцениваются их средние абсолютные погрешности или средние квадратичные погрешности .

Средняя абсолютная погрешность косвенных измерений физической величины  вычисляется по формуле



где  - частные производные от φ поx, y, z, вычисленные для средних значений соответствующих аргументов.

Так как в формуле использованы абсолютные величины всех членов суммы, то выражение для оценивает максимальную погрешность измерения функции при заданных максимальных ошибках независимых переменных.

Средняя квадратичная погрешность косвенных измерений физической величины 



Относительная максимальная погрешность косвенных измерений физической величины 



где и т. д.

Аналогично можно записать относительную среднюю квадратичную погрешность косвенных измерений 

Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять максимальную относительную погрешность косвенных измерений . Для этого (в случае средней абсолютной погрешности) надо проделать следующее.

1. Прологарифмировать выражение для косвенного измерения физической величины.

2. Продифференцировать полученное выражение.

3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.

4. Взять выражение перед различными дифференциалами по модулю (в соответствии с теорией Гаусса погрешности складываются по абсолютной величине).

5. Формально заменить значки дифференциалов на значки абсолютной погрешности .

Затем, зная , можно вычислить абсолютную погрешность  по формуле

 = 
Пример 1. Вывод формулы для вычисления максимальной относительной погрешности косвенных измерений объёма цилиндра.

Выражение для косвенного измерения физической величины (исходная формула)



Величина диаметра D и высоты цилиндра h измеряются непосредственно приборами с погрешностями прямых измерений соответственно D и h.

Прологарифмируем исходную формулу и получим



Продифференцируем полученное уравнение



Заменив значки дифференциалов на значки абсолютной погрешности , окончательно получим формулу для расчёта максимальной относительной погрешности косвенных измерений объёма цилиндра

4. Правила представления результатов измерения

• 
  Результаты измерения принято представлять в виде или
  
• 
  Погрешность должна округляться до одной значащей цифры:
  

правильно –  = 0,04,

неправильно –  = 0,0382.

• 
  Последняя значащая цифра результата должна быть того же порядка величины, что и погрешность:
  

правильно –  = 9,830,03,

неправильно –  = 9,8260,03.

• 
  Если результат имеет очень большую или очень малую величину, необходимо использовать показательную форму записи - одну и ту же для результата и его погрешности, причем запятая десятичной дроби должна следовать за первой значащей цифрой результата:
  

правильно –  = (5,270,03)10^-5,

неправильно –  = 0,00005270,0000003.

• 
  Если результат имеет размерность, ее необходимо указать:
  

правильно – g = (9,820,02) м/c²,

неправильно – g = (9,820,02).

5. Правила построения графиков

1. Графики строятся с использованием компьютера.

2. Перед построением графика необходимо четко определить, какая переменная величина является аргументом, а какая функцией. Значения аргумента откладываются на оси абсцисс (ось х), значения функции - на оси ординат (ось у).

3. Из экспериментальных данных определить пределы изменения аргумента и функции.

4. Указать физические величины, откладываемые на координатных осях, и обозначить единицы величин.

5. На осях координат указать масштаб (при очень больших или очень малых величинах, показательную часть в записи величины указать рядом с единицами измерений на оси).

6. Нанести на график экспериментальные точки, обозначив их (крестиком, кружочком, жирной точкой).

7. Провести через экспериментальные точки плавную линию, в соответствии с выбранным законом аппроксимации экспериментальных данных, по методу наименьших квадратов.

6. Содержание отчета

Отчёт оформляется в печатном виде на листах формата А4 в соответствии с требованиями, предъявляемыми кафедрой ОТФ, в котором помимо стандартного титульного листа должны быть раскрыты следующие пункты:

1. 
   Цель работы.
   
2. 
   Краткое теоретическое содержание.
   

1. 
   Явление, изучаемое в работе.
   
2. 
   Определение основных физических понятий, объектов, процессов и величин.
   
3. 
   Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчётные формулы.
   
4. 
   Пояснения к физическим величинам и их единицы измерений.
   

3. 
   Схема установки.
   
4. 
   Расчётные формулы.
   
5. 
   Формулы погрешностей косвенных измерений.
   
6. 
   Таблицы с результатами измерений и вычислений. (Таблицы должны иметь номер и название. Единицы измерения физических величин должны быть указаны в отдельной строке.)
   
7. 
   Пример вычисления (для одного опыта).
   

1. 
   Исходные данные.
   
2. 
   Вычисления.
   
3. 
   Окончательный результат.
   

8. 
   Графический материал.
   

1. 
   Аналитическое выражение функциональной зависимости, которую необходимо построить.
   
2. 
   На осях координат указать масштаб, физические величины и единицы измерения.
   
3. 
   На координатной плоскости должны быть нанесены экспериментальные точки.
   
4. 
   По результатам эксперимента, представленным на координатной плоскости, провести плавную линию, аппроксимирующую функциональную теоретическую зависимость в соответствии с методом наименьших квадратов.
   

9. 
   Анализ полученного результата. Выводы.
   

ПРИЛОЖЕНИЕ 2

Метод наименьших квадратов
Суть метода заключается в поиске такой функциональной зависимости у = (х, с₁, с₂, ..., с_m) с коэффициентами с_j(j = 1,2,...,m), при которой сумма

                      (1)

будет минимальна. Здесь у_i - совокупность экспериментальных значений функции.

В соответствии с необходимым условием экстремума функций нескольких переменных, нужно приравнять к нулю частные производные суммы (1) по каждому из коэффициентов, т.е.

                  (2)

Полученные уравнения (2) для нахождения коэффициентов с_j называются нормальными уравнениями для выбора наилучшего приближения к экспериментальным данным.

Если аппроксимирующая функция может быть представлена в виде линейной комбинации функций



(здесь _j(x) - известные функции), то аппроксимация называется линейной.

Рассмотрим использование метода на примере наиболее простой, линейной зависимости. Если две переменные у и х связаны зависимостью типа у = А + Вх, то график такой функции, как известно, представляет собой прямую, наклон которой к оси абсцисс определяется коэффициентом В = tg, а точка пересечения ординаты .

На практике каждое измерение х_i и у_i сопровождается погрешностью. На рис. показаны экспериментальные точки с учетом погрешности при наличии линейной зависимости.

Можно провести множество прямых, которые близко проходят около этих точек. Метод наименьших квадратов позволяет подобрать такие коэффициенты А и В, что аппроксимация экспериментальных точек прямой у = f(х, А, В) будет наилучшей с точки зрения выполнения условия (1). Это условие предполагает в качестве критерия наилучших значений А и В такие, при которых вероятность получения всего данного набора результатов измерений у_i(i = 1,2,...,N) максимальна.

Предположим, что результат измерения каждого значения у_i подчиняется распределению Гаусса и средняя квадратическая погрешность _у одинакова для всех измерений. Согласно теории вероятности, вероятность получения значения у_i

, (3)

где y_i = A + Bx_i - истинное значение измеряемой величины при значении аргумента x_i.

Вероятность получения всего набора результатов измерений у₁, у₂, ..., у_N равна произведению соответствующих вероятностей:

… (4)

где



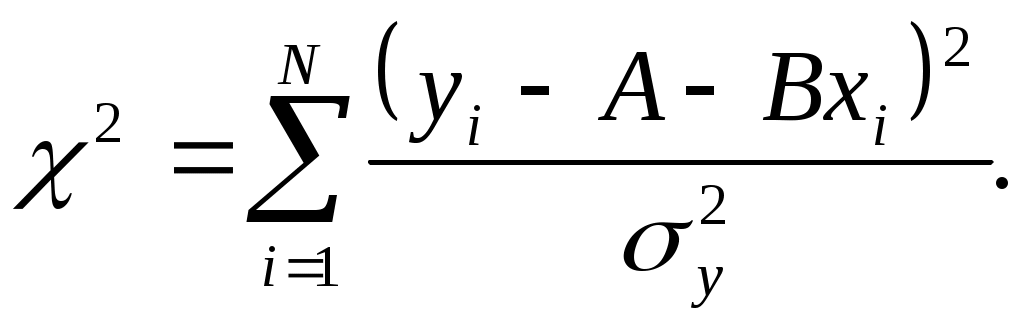
Из формулы (4) следует, что вероятность максимальна, когда значение минимально. Причем, если постоянно для всех y_i, то минимальной должна быть сумма



Итак, мы вернулись к условию (14), введенному в общем виде для любой функциональной зависимости.

Расчет величин А и В. В соответствии с уравнениями (2) приравняем производные по коэффициентам А и В к нулю:



Тогда



(5)


 (6)
В результате решения системы нормальных уравнений (5) и (6) получим наилучшие оценки постоянных А и В для прямой у = А + Вх, основанные на измеренных точках x_i, y_i:

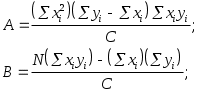(7)

где

Погрешность в измерениях у. Не вдаваясь в довольно сложные теоретические рассуждения, приведем формулу для расчета погрешности _у при наличии линейной аппроксимации у = А +Вх:

(8)

где А и В определяются по формуле (7).

Если в опыте произведено только два измерения, то _у = . Это означает, что при обработке данных опыта методом наименьших квадратов необходимо, чтобы число опытов было по крайней мере больше двух.

Погрешность постоянных А и В. Величины А и В рассчитывают на основании экспериментальных данных x_i и y_i. Так как каждое измерение x_i и y_i сопровождается погрешностью, то и величины А и В имеют погрешности _А и _В. Их рассчитывают по формулам

ПРИЛОЖЕНИЕ 3.

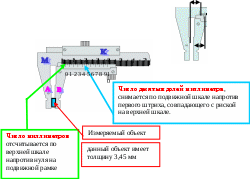
Штангенциркуль

Штангенциркуль предназначен для измерения длины до 150-500 мм, с точностью до 0.1 или 0.05 мм.

Штангенциркуль состоит из масштабной линейки – М с выступом А, называемым губкой, и подвижной рамки К, с другой губкой В. Рамка передвигается вдоль масштабной линейки, часть рамки снабжена нониусом.

Измеряемый объект зажимается между губками масштабной линейки и рамки.

Нуль масштабной линейки смещен на некоторое расстояние от плоскости губки А, на такое же расстояние смещен и нуль нониуса относительно плоскости губки В на рамке К. Таким образом, измеряемая длина предмета равна расстоянию между нулем масштабной линейки и нулем нониуса.
Снятие отсчета.




Микрометр.

Микрометр используется для измерения небольших значений длины до 25-50 мм и более с точностью до 0.01 мм.

Микрометр состоит из микрометрического винта А, ввинченного в скобу Е.

Измеряемое тело помещается между плоскостями торца А и упора А', укрепленного в скобе.


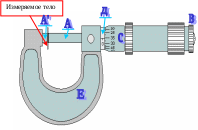
Шаг винта А равен 0,5 мм. На барабане С имеется лимб, разбитый на 50 равных делений. При вращении барабана он переме-щается вдоль шкалы Д, цена деления которой равна 0,5 мм, т.е. шагу винта А. Таким образом, цена деления лимба барабана 0,01 мм.



Измерение микрометром производят следующим образом: вращая винт А за головку В, прижимают измеряемый предмет к упору А' затем берут отсчет по неподвижной шкале Д с точностью до 0,5 мм и прибавляют сотые доли миллиметра, которые отсчитывают по делениям лимба барабана С.

Число сотых отсчитывают по штриху лимба, находящемуся против продольного штриха шкалы Д.