Раздел долгосрочного плана:
6.2А. Действия над рациональными числами
|
Школа: КГУ «Чувашинская СОШ»
|
Дата:
|
ФИО учителя: Темирбаева И.Б.
|
Класс: 6
|
Количество присутствующих:
|
отсутствующих:
|
Тема урока
|
Умножение рациональных чисел
|
Цели обучения, которые достигаются на данном уроке
|
6.1.2.15 выполнять умножение рациональных чисел;
|
Цели урока
|
Учащиеся будут:
- выполнять умножение рациональных чисел;
- применять свойстваумножения рациональных чисел
|
Критерии оценивания
|
Учащийся:
–определяет порядок действий числовых выражений;
-применяет правила умножения рациональных чисел;
–находит значение числового выражения;
- использует свойства умножения рациональных чисел.
|
Языковые цели
|
Учащиеся будут:
комментировать свои решения, используя правила умножения над рациональными числами;
описывать устно алгоритм действий над рациональными числами.
Предметная лексика и терминология:
Натуральные числа;
Целые числа;
Обыкновенные дроби;
Положительные числа;
Отрицательные числа;
Положительные числа;
Десятичные дроби;
Рациональные числа;
сумма;
разность;
произведение;
частное;
числовые выражения
|
Привитие ценностей
|
Уважение к себе и другим и сотрудничество – через работу в паре, в группе, академическая честность – при самостоятельной работе, открытость – учащиеся самостоятельно могут определить цели урока и задачи.
|
Межпредметные связи
|
Применение рациональных чисел в практической жизни человека.
|
Предварительные знания
|
Знание понятия рационального числа и умение выполнять арифметические действия с рациональными числами.
|
Ход урока
|
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
|
Организация начала урока
Приветствие. «Ладошки»
Учащиеся поочередно касаются одноименных пальцев рук своего соседа, начиная с больших пальцев и говорят:
желаю (соприкасаются большими пальцами);
успеха (указательными);
большого (средними);
во всём (безымянными);
и везде (мизинцами);
Здравствуйте! (прикосновение всей ладонью)
Выборочная проверка домашнего задания.
|
|
Начало урока
|
В качестве повторения ранее изученного материала применяется игра «Да» - «Нет». Вопрос читается один раз, переспрашивать нельзя, за время чтения вопроса необходимо записать ответ «да» или «нет». Учащиеся меняются тетрадями в парах за партой и проверяют друг у друга ответы. С какими утверждениями вы не согласились?
Игра «Да - нет»
1.Два числа, отличающиеся друг от друга только знаками, называются противоположными числами.
2. Для каждого числа есть два противоположных ему числа. -
3.Модулем числа а называют расстояние от начала отсчёта до точки, изображающей это число на координатной прямой.
4.Модуль числа 0 равен нулю.
5.Модуль числа может быть отрицательным.
6.Противоположные числа имеют разные модули.
7.Из двух отрицательных чисел меньше то, модуль которого больше.
8.Нуль меньше любого отрицательного числа.
9.Нуль меньше любого положительного числа.
10.Если к любому числу прибавить нуль, то число не изменится.
ФО Взаимопроверка по готовым ответам
Дифференциация: по темпу
Задание «Найди ошибку».
Учащиеся получают карточки и выясняют какие правила нарушены, что неверно, исправляют ошибки и аргументируют выбор.
Исправь ошибки!
-4 + 7 = -11
- 3 + 14 = - 11
- 2,3 + (- 2,1) = - 0,2
11 – 19 = 8
- 15 – (- 30) = - 45
3 + (- 0,5) = 2,5
- 5 + (- 3) = - 8
- 4 – 2 = - 2
Какие правила здесь нарушены, что неверно, исправь ошибки и докажи.
Учащиеся повторяют правила сложения и вычитания чисел с разными знаками.
ФО через обратную связь: конструктивный комментарий учителя
Дифференциация: по заданиям
|
Приложение 1
|
Середина урока
|
Коллективная работа.
Задача:
Уровень воды в реке каждые сутки меняется на 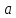 см. см.
Как изменится уровень воды в реке за 6 суток, если 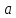 = 2; = 2; 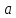 = –7? = –7?
-Составьте выражение для решения задачи.
-Найдите значение выражения при заданных значениях переменной.
- Сформулируйте правило умножения отрицательного числа на положительное число.
ФО Комментарий учителя
Дифференциация: Диалог и оказание поддержки
Пример:
Вычислить: –5 ∙ (–10) = 500.
сформулируйте правило умножения отрицательных чисел.
ФО Комментарий учителя
Дифференциация: Диалог и оказание поддержки
Сделайте вывод правила умножения двух чисел.
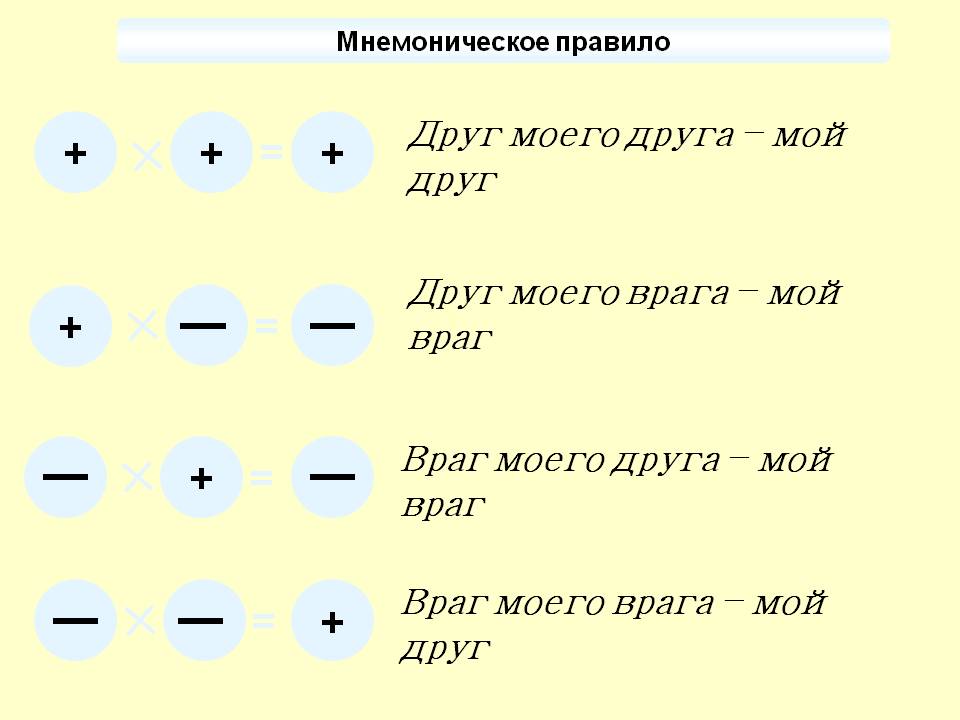
Учащиеся приводят примеры.
Определите знак произведения и вычислите:
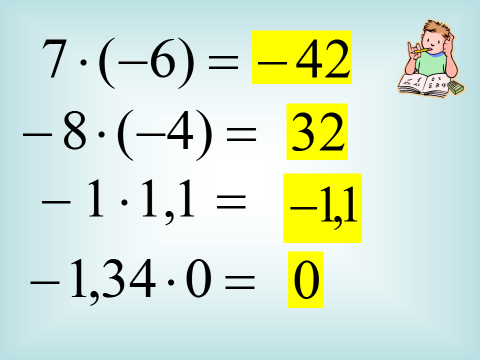
Какой вывод можно сделать относительно знака произведения, где чётное (нечётное) число отрицательных множителей?
Вывод: 1. Если число отрицательных множителей нечетное, то произведение - число отрицательное.
Учащиеся приводят примеры.
Вывод 2.Если число отрицательных множителей чётное, то произведение - число положительное.
Учащиеся приводят примеры.

Учащиеся приводят примеры.
3.Работа в парах (дифференцированные задания на карточках)
Выполните умножение:
1 вариант
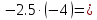
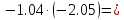
-1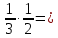
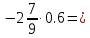
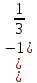
2 вариант
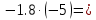
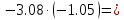
2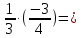
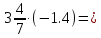
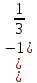
Дескрипторы: Учащиеся
- умножают рациональные числа с разными знаками
- -умножают рациональные числа с одинаковыми знаками
-умножают рациональные числа, используя правила
Обмен тетрадями в парах и оценивание «Две звезды одно пожелание»
Дифференциация: по заданиям
4. Закрепление.
Индивидуальная работа (тест по карточкам)
Задания:
№1. Укажите выражения, значения которых равны 24:
а) -12•2; б) (-4)•6; в) (-8)•(-3); г) -24•(-1).
№2. Укажите выражения, значения которых равны -32:
а) 16•(-2); б) (-4)•(-8); в) (-16)•2; г) -32•(-1)
№3. Значение произведения 2•(-0,2)•(-5) равно:
а) 20; б) 2; в) -20; г) -2.
№4 Значение произведения -3•(-0,4)•(-5) равно:
а) 60; б) -60; в) -6; г) 6.
№5 . Вычислите (-2)3:
а) 8; б) -8; в) 6; г) -6.
№6. Вычислите (-3)2:
а) 6; б) -6; в) 9; г) -9.
Дескрипторы: Учащиеся
- умножают рациональные числа с разными знаками
- умножают рациональные числа с одинаковыми знаками
- умножают рациональные числа, используя правила.
ФО Самопроверка по ключу
Дифференциация: по заданиям
|
Приложение 2
Приложение 3
|
Конец урока.
|
Рефлексия: «SMS»
Ученикам предлагается на бумажных сотовых телефонах написать SMS – сообщение о том,
как прошёл урок, оценить, как плодотворно он работал.
По результатам SMS сообщений учащихся учитель планирует дальнейшие уроки.
Разноуровневое домашнее задание.
|
Т.А. Алдамуратова, К.С. Байшоланова, Е.С. Байшоланов, Алматы: «Атамұра» 2018 г. 1 часть
|
 Скачать 150.76 Kb.
Скачать 150.76 Kb.