Геодезия КР№1. Геодезия КР№1 Ляжьев Я.А ПХ-210(КЖТЗ). Уральский государственный университет путей сообщения
 Скачать 157.02 Kb. Скачать 157.02 Kb.
|
|
Федеральное агентство железнодорожного транспорта «Уральский государственный университет путей сообщения» Колледж железнодорожного транспорта КОНТРОЛЬНАЯ РАБОТА №1 по дисциплине «Геодезия» на тему «Обработка материалов геодезических измерений, выполненных при создании планового съемочного обоснования» Проверил: Выполнил: Старший преподаватель студент группы ПХ-210 Шишов А.М. Ляжьев Я.А. Екатеринбург 2022 год Содержание Пояснительная записка 3 План местности 16 Пояснительная записка к контрольной работе №1 «Обработка материалов геодезических измерений, выполненных при создании планового съемочного обоснования» Исходные данные Индивидуальные исходные данные: дирекционный угол α = 117°40ʹ; координаты точки 1 Х = 1150,00 м Y = 1000,00 м. Общие исходные данные: горизонтальные углы и горизонтальные проложения, выписанные в специальную ведомость. Уравнивание теодолитного хода Уравнивание– это процесс обработки измерений, в результате которого: производят контроль и оценку точности измерений; получают наиболее вероятные значения измеренных величин и их функций. Уравнивание горизонтальных углов Выполняю в графах 2 и 3 в следующем порядке: а) вычисляю сумму измеренных углов Σ β изм = 97°58,0´ + 91°24,5´ + 77°31,0´ + 93°05,5´ = 359°59,0´ б) вычисляю теоретическое значение этой суммы по формуле Σ β т = 180 · ( 4 – 2 ), где n – число точек хода Σ β т = 180 · ( 4 – 2 ) = 360°00,0´ в) вычисляю угловую невязку хода f β = Σ β изм - Σ β т f β = 359°59,0´ - 360°00,0´ = - 1,0´ г) вычисляю допустимое значение данной невязки доп. f β = 1´ √(n) доп. f β = 1´ √(4) = ± 2,0´ д) сравниваю полученную невязку с допустимой | - 1,0 | ˂ | ± 2,0 | | f β | ˂ доп. f β Распределяю невязку с обратным знаком по измеренным углам, округляя поправки δ β до 0,5´. Поправки выписываю над измеренными углами в графе 2. Контроль вычисления поправок: Σ δ β = - f β Σ δ β = 0,5 + 0,5 = 1,0 1,0 = - ( - 1,0 ) Следовательно, поправки вычислены верно. г) вычисляю уравненные значения углов и их сумму в графе 3 91°24,5´ + 0,5 = 91°25´ 93°05,5´ + 0,5 = 93°06´ Контроль: 97°58´ + 91°25´ + 77°31´ + 93°06´= 360°00,0´ = Σ β т Следовательно, уравненные углы найдены верно. Вычисление дирекционных углов сторон хода Дирекционные углы сторон хода вычисляю в графе 4 по заданному дирекционному углу начальной стороны ɑ1-2 и уравненным значениям горизонтальных углов (правых) по формуле передачи дирекционного угла: ɑ k + 1 = ɑ k + 180° - β, где ɑ k + 1 – дирекционный угол последующей стороны хода, ɑ k – дирекционный угол предыдущей стороны, β – правый по ходу горизонтальный угол между этими сторонами. ɑ 1 - 2 = 117°40´ + 180° - 97°58´ = 199°42´ ɑ 2 - 3 = 199°42´ + 180° - 91°25´ = 288°17´ ɑ 3 - 4 = 288°17´ + 180° - 77°31´ = 390°46´ Так как при вычислении величина дирекционного угла ɑ 3 – 4 оказалась больше 360°, то вычитаю из результата 360°: ɑ 3 - 4 = 390°46´ - 360° = 30°46´ ɑ 4 - 1 = 30°46´ + 180° - 93°06´ = 117°40´ Контроль вычислений: использовав все углы замкнутого хода из графы 3, снова получаю заданное значение дирекционного угла. Следовательно, дирекционные углы сторон хода мною вычислены верно. Вычисление и уравнивание приращений координат Выполняю данные вычисления в графах 6 – 9. Для этого использую формулы: Δ х = d · cos ɑ Δ y = d · sin ɑ, где d - горизонтальное проложение стороны хода, ɑ - дирекционный угол той же стороны. Вычисляю значения приращений координат: ɑ 1 - 2 = 117°40´ Δ х = 135,48 · cos (117°40´) = - 62,90 Δ у = 135,48 · sin (117°40´) = 119,98 ɑ 2 - 3 = 199°42´ Δ х = 163,02 · cos (199°42´) = - 153,47 Δ у = 163,02 · sin (199°42´) = - 54,95 ɑ 3 - 4 = 288°17´ Δ х = 170,80 · cos (288°17´) = 53,58 Δ у = 170,80 · sin (288°17´) = - 162,17 ɑ 4 - 1 = 30°46´ Δ х = 189,70 · cos (30°46´) = 163,00 Δ у = 189,70 · sin (30°46´) = 97,03 Вычисленные значения приращений координат со своими знаками выписываю в графы 6 и 7. В суммарной строке этих же граф нахожу координатные невязки: Σ Δ х = - 62,90 - 153,47 + 53,58 + 163,00 = 0,21 Σ Δ у = 119,98 - 54,95 - 162,17 + 97,03 = - 0,11 Следовательно, координатные невязки равны f х = 0,21 f у = - 0,11 В суммарной строке графы 5 записываю значение периметра хода с точностью до метра: Р = 135,48 + 163,02 + 170,80 + 189,70 = 659,0 м Для оценки допустимости координатных невязок вычислю невязку f р в периметре хода и относительную невязку f р / р, сохраняя в ее знаменателе две значащие цифры: f р = √ (f х² + f у²) f р = √ ( (0,21)² + (- 0,11)²) = 0,24 f р / р = 0,24 / 659 = 1 / 2700 Оценка допустимости координатных невязок: 1 / 2700 ˂ 1 / 2000 Следовательно, координатные невязки допустимы. Распределяю их с обратным знаком по всем приращениям пропорционально длинам сторон хода по формулам прямой пропорциональной зависимости: δ хi = ( - f х ) : Р · di δ уi = ( - f у ) : Р · di δ х1 = 0,21 : 659 · 135,48 = 0,05 δ х2 = 0,21 : 659 · 163,02 = 0,05 δ х3 = 0,21 : 659 · 170,80 = 0,05 δ х4 = 0,21 : 659 · 189,70 = 0,06 Контроль вычисления поправок: Σ δ хi = 0,05 + 0,05 + 0,05 + 0,06 = 0,21 Σ δ хi = - f х ; следовательно, поправки вычислены верно. δ у1 = - 0,11 : 659 · 135,48 = - 0,02 δ у2 = - 0,11 : 659 · 163,02 = - 0,03 δ у3 = - 0,11 : 659 · 170,80 = - 0,03 δ у4 = - 0,11 : 659 · 189,70 = - 0,03 Контроль вычисления поправок: Σ δ уi = - 0,02 - 0,03 - 0,03 - 0,03 = - 0,11 Σ δ уi = - f у ; следовательно, поправки вычислены верно. Поправки в сантиметрах выписываю над приращениями координат в графах 6 и 7. В графах 8 и 9 вычисляю уравненные приращения координат, учитывая их знак и знак поправки: Δ х´ : - 62,90 - 0,05 = - 62,95 - 153,47 + 0,05 = - 153,52 53,58 - 0,05 = 53,53 163,00 - 0,06 = 162,94 Δ у´ : 119,98 + 0,02 = 120,00 - 54,95 - 0,03 = - 54,92 - 162,17 - 0,03 = - 162,14 97,03 + 0,03 = 97,06 Контроль правильности вычисления уравненных приращений: Σ Δ х´ = - 62,95 - 153,52 + 53,53 + 162,94 = 0 Σ Δ у´ = 120,00 - 54,92 - 162,14 + 97,06 = 0 Σ Δ х´ = 0, Σ Δ у´ = 0, следовательно, уравненные приращения вычислены верно. Вычисление координат точек хода По заданным координатам точки 1 и уравненным приращениям координат вычисляю координаты всех точек хода по формулам: х k + 1 = х k + Δ х´ у k + 1 = у k + Δ у´ х 1 = 1150,00 х2 = 1150,00 + 62,95 = 1212,95 х3 = 1212,95 + 153,52 = 1366,47 х4 = 1366,47 - 53,53 = 1312,94 х 1 = 1312,94 - 162,94 = 1150,00 у1 = 1000,00 у2 = 1000,00 + 120,00 = 1120,00 у3 = 1120,00 - 54,92 = 1065,08 у4 = 1065,08 - 162,14 = 902,94 у1 = 902,94 + 97,06 = 1000,00 Контроль вычислений: использовав все приращения координат из граф 8 и 9, получаю снова заданные координаты первой точки; следовательно, координаты точек хода вычислены верно. Ведомость вычисления координат точек съемочного обоснования
Σ 359°59,0´ 360°00,0´ 659 0,21 - 0,11 0 0
Составление плана горизонтальной съемки в масштабе 1:2000 Исходные данные - координаты точек теодолитного хода, найденные выше х1 = 1150,00 м у1 = 1000,00 м х2 = 1212,95 м у2 = 1120,00 м х3 = 1366,47 м у3 = 1065,08 м х4 = 1312,94 м у4 = 902,94 м - абрис и журнал съемки с точки 3. Построение координатной сетки На листе чертежной бумаги формата А4 проведу две диагонали. От точки их пересечения на полудиагоналях откладываю равные отрезки длиной 13 см. Соединив полученные точки, получаю исходный прямоугольник АВСД. Чтобы теодолитный ход разместился в средней части чертежа, выполню расчет положения координатных линий. Для этого стороны АВ и АД исходного прямоугольника делю примерно пополам и получаю точки a и b. С точностью до целых метров вычисляю координаты этих точек по формулам: х а = (х max + x min) : 2 = (1366,47 + 1150,00) : 2=1258,23 м у b = (у max + у min) : 2 = (1120,00 + 902,94) : 2 =1011,47 м. Вычисляю расстояния от точек a и b до ближайших южной (нижней) и западной (левой) координатных линий, кратных 200 м: Δ х = 1258,23 – 1200 = 58,23 м или 29,11 мм в масштабе 1 : 2000; Δ у = 1011,47 – 1000 = 11,47 м или 5,73 мм в масштабе 1 : 2000. Расстояние Δ х откладываю от точки a вниз, а Δ у от точки b влево, получая точки cи d, через которые пройдут искомые координатные линии. Для точного построения координатных линий беру измерителем отрезок Ас, откладываю его от точки Д по стороне ДС исходного прямоугольника и накалываю точку с´. Через точки си с´ провожу горизонтальную координатную линию, абсцисса которой в моем случае равна 1200 м. Затем получаю точку d ´, откладывая измерителем отрезок Аd от точки В вдоль стороны ВС. Через точки dи d´ провожу вертикальную координатную линию, ордината которой в моем случае равна 1000 м. От полученных точек с и с´, d и d ´ откладываю отрезки по 10 см и провожу остальные координатные линии. Дальнейшие построения выполняю на полученной таким образом координатной сетке. Для контроля измеряю диагонали полученных квадратов и прямоугольников. Расхождение диагоналей в каждой фигуре не превышает 0,2 мм, следовательно, координатные линии построены верно. Точки пересечения всех координатных линий накалываю. Все дальнейшие построения выполняю от этих наколов. На координатных линиях надписываю их абсциссы и ординаты. Нанесение точек теодолитного хода Для упрощения работу составляю таблицу 2 подготовки данных. В нее выписываю координаты точек, округленные в пределах точности масштаба (0,2 м). Таблица 2 Подготовка данных для построения точек хода
Построение точек хода выполняю с помощью измерителя и точной линейки от ближайших линий координатной сетки. Получив на плане первые две точки хода, проверяю правильность их нанесения. Для этого измеряю длину линии между точками и сравниваю ее с записанной в ведомости вычисления координат. Таким же образом проверяю правильность построения всех последующих точек хода. Результаты контроля отражаю в таблице 3. Таблица 3 Контроль правильности построения точек хода
Допуск 0,3 мм Расхождение не превышает 0,3 мм. Следовательно, точки хода нанесены правильно. 2.4 Построение контурных точек, составление и оформление плана Построение контурных точек выполняю по данным абриса и журнала съемки (см. рисунок 1) с помощью линейки, транспортира и угольника. Точки наношу в следующем порядке: Обхожу весь ход, строя точки, снятые способом пересечения линий хода с контурами; Соединив одноименные точки на линиях 2 - 3 и 4 - 1 хода, строю линию связи, ЛЭП, железную дорогу; Транспортиром строю полярные углы при точке 3 по данным журнала съемки; По полученным с точки 3 направлениям откладываю указанные в журнале расстояния; Строю контур кустарника, положение первых столбов; Провожу проселочную дорогу, строю остальные столбы по указанным на абрисе расстояниям между ними, наношу переезд; Способом перпендикуляров строю здания. 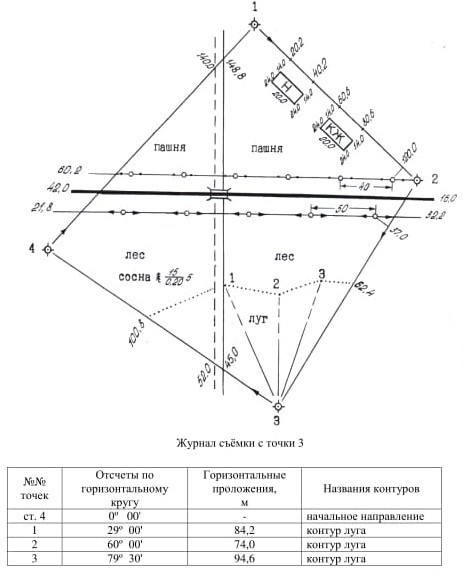 Рис.1 Абрис и журнал съемки с точки 3 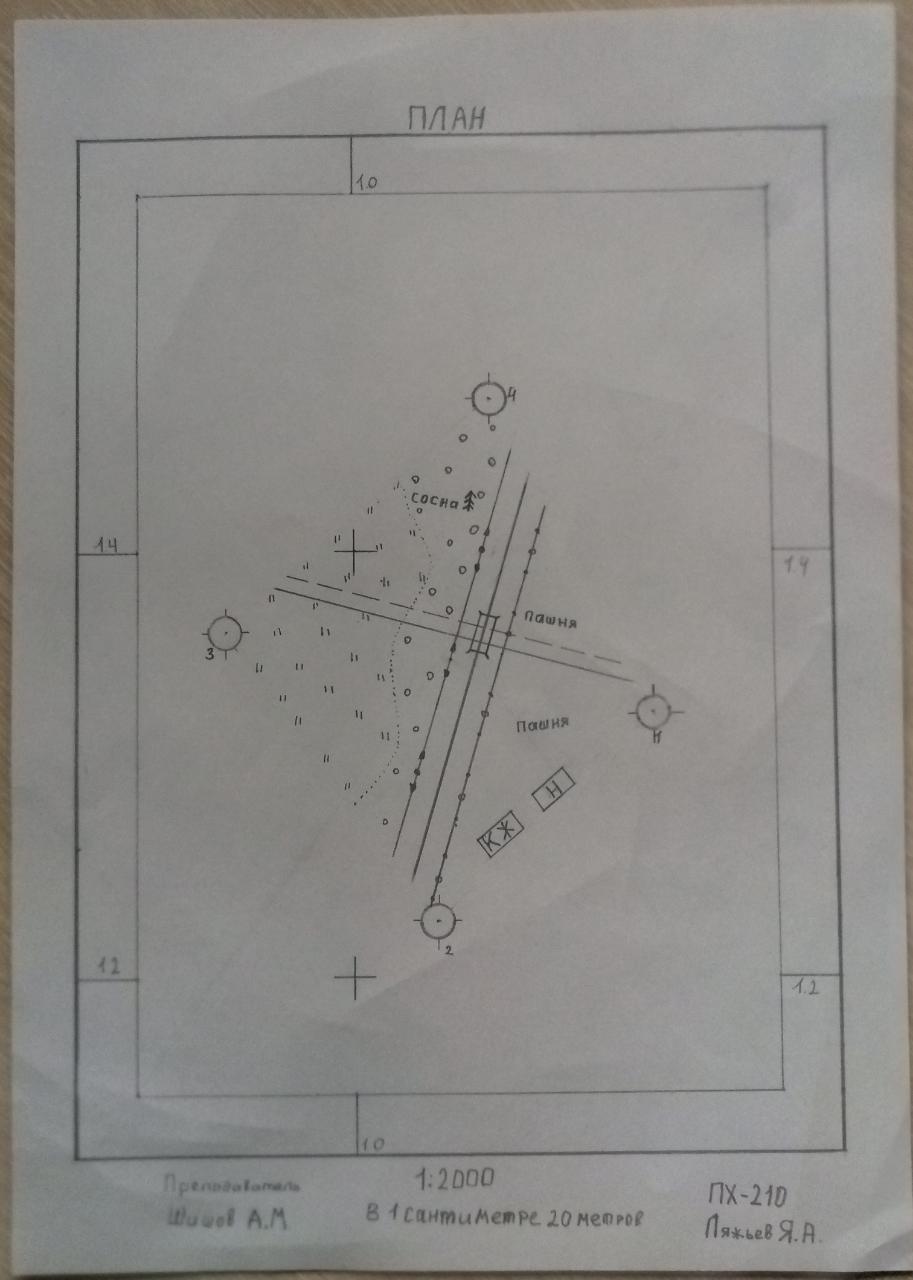   | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
