уравнение берталанфи. Уравнение Берталанфи
 Скачать 133.3 Kb. Скачать 133.3 Kb.
|
 Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное учреждение высшего образования «Астраханский государственный технический университет» Институт рыбного хозяйства, биологии и природопользования Направление «Водные биоресурсы и аквакультура» РЕФЕРАТ на тему: «Уравнение Берталанфи» Работу выполнил Студент группы: ЗРВА-21 Мансимли А.А. Работу проверила: Сорокина М.Н. Астрахань 2021 г. Содержание: Введение 3 Глава 1. Биография Берталанфи 4 Глава 2. Уравнение линейного роста Берталанфи 7 Заключение. 12 Литература 13 Введение В морских и внутренних водоемах видовой состав промысловых уловов часто весьма разнообразен, но существующая промысловая статистика, как правило, не дает верного представления о действительном соотношении видов. Такие данные промысловой статистики, неправильно отражая действительное соотношение видов рыб, особенно младших возрастов, могут стать причиной серьезных ошибок как при оценке запасов и планирования уловов на ближайшие годы, так и при разработке мероприятий охранного характера. Поэтому регулярные анализы видового, размерного и возрастного состава промысловых уловов – задача столь же важная и необходимая, как изучение возраста и темпа роста рыб, возраста наступления половой зрелости и других биологических показателей. Основным источником ихтиологических материалов являются промысловые уловы. Так как в крупных водоемах промысел обычно круглогодичный, но интенсивность его в разные сезоны неодинакова, сбор основного ихтиологического материала необходимо приурочить прежде всего к главным сезонам промысла. На малых водоемах, где регулярного промысла нет, ихтиологические материалы следует собирать во время облова водоемов. О состоянии запасов той или иной рыбы в водоеме судят, прежде всего, по величине уловов за ряд последних лет, по количественному соотношению возрастных групп, возрасту наступления первой и массовой половозрелости, который, в свою очередь, зависит от темпа роста рыб Людвиг фон Берталанфи  Карл Людвиг фон Берталанфи (19 сентября 1901 - 12 июня 1972) Австрийский биолог известен как один из основателей общая теория систем (GST). Это междисциплинарная практика, описывающая системы с взаимодействующими компонентами, применимая к биология, кибернетика и другие поля. Берталанфи предположил, что классический законы термодинамики может применяться к закрытым системам, но не обязательно к «открытым системам», таким как живые существа. Его математическая модель исследования роста организма с течением времени, опубликованная в 1934 году, используется до сих пор. Берталанфи вырос в Австрии и впоследствии работал в Вена, Лондон, Канада, а Соединенные Штаты. Знаменитый австрийский философ и биолог-теоретик, создатель «общей теории систем». Берталанфи родился в г. Ацгерсдорф, в Австрии. Получил биологическое образование в Венском университете. С 1934 г. по 1948 г. Берталанфи работал доцентом, а затем профессором Венского университета. С 1949 г. по 1961г. он работал в различных университетах США и Канады, а с 1961 г. был профессором теоретической биологии университета Альберта (Канада). Подходя к биологическим объектам как к организованным динамическим системам, Берталанфи дал развёрнутый анализ возникновения и развития организмических идей о целостности организма и на основе последних — формирования системных концепций в биологии. Предложенный им метод анализа открытых эквифинальных (т. е. стремящихся к некоторой цели) систем дал возможность широко использовать в биологии идеи термодинамики и кибернетики. Идеи Берталанфи нашли применение в медицине, психиатрии и др. прикладных дисциплинах. Берталанфи выдвинул первую в современной науке обобщённую системную концепцию, задачами которой стали разработка математического аппарата описания разных типов систем, установление изоморфизма законов в различных областях знания и поиск средств интеграции науки. Будучи активным пропагандистом системного подхода, он стал одним из главных организаторов «Общества по исследованиям в области общей теории систем» (создано в 1954г. ) и его ежегодника «General Systems». Основные положения этой теории были сформулированы накануне второй мировой войны. Кратко они утверждали следующее: “Существуют модели, принципы и законы, которые применимы к обобщенным системам, или к подклассам систем, безотносительно к их конкретному виду, природе составляющих элементов и отношениям, или силам, между ними... Общая теория систем представляет собой логико-математическую область исследований, задачей которой является формирование и выведение общих принципов, применяемых к системам вообще. Осуществляемая в рамках этой теории точная формулировка таких понятий, как целостность и сумма, дифференциация, централизация, иерархическое строение, финальность и эквифинальность, позволяет сделать эти понятия применимыми во всех дисциплинах, имеющих дело с системами, и установить их логическую гомологию”. В послевоенные годы Берталанфи предлагает математическое описание системных параметров (целостность, эквифинальность и др.), с помощью одновременных дифференциальных уравнений. Эти уравнения он называет динамическими или уравнениями движения, полагая, что их совокупность дает полное описание поведения любой системы. Берталанфи особенно отмечает тот факт, что системные законы проявляются в виде аналогий или “логических гомологий”, законов, представляющихся формально идентичными, но относящимися к совершенно различным явлениям или дисциплинам. Занимаясь биологической проблематикой, Берталанфи иллюстрирует эти положения примерами, взятыми из биологии, типа аналогии между центральной нервной системой и сетью биохимических клеточных регуляторов. Очевидно, что подобным примером служит и приведенная ранее аналогия между психофизическими и термодинамическими закономерностями. Не менее важным аспектом теории систем является решение проблемы устойчивости, т.е. реакции системы на деформацию. Для решения этой проблемы Берталанфи также предложил математический метод, опирающийся на анализ описывающих систему дифференциальных уравнений. Количественным показателем развития рыб является их рост. Поэтому математическая оценка количественных параметров роста в естественных условиях имеет первостепенное значение при изучении динамики рыбных ресурсов и разработке мероприятий по их рациональному использованию. Уравнение линейного роста Берталанфи Для количественной оценки параметров роста рыб чаще всего используют - Уравнение линейного роста Берталанфи l(t) = L(1− e−K (t−t 0)) ,(1) где l(t) – длина рыбы в момент времени t; L – средняя предельная длины рыбы исследуемой популяции; K – константа, характеризующая скорость изменения длины; t0 – константа, указывающая момент времени, в который длины рыбы в принятой модели роста (1) была равна нулю; (t – t0) – время, прошедшее от рождения рыбы (возраст рыбы). Уравнение (1) позволяет для заданного возраста рыбы определить ее длину или прирост длины за фиксированный отрезок времени (год, сезон и т.д.), оно используется для нахождения индивидуального и популяционного роста особей промыслового стада, расчете продукционных характеристик и т.д. В уравнении (1) содержится три неизвестных коэффициента L, K и t0, которые должны быть определены на основе экспериментальных измерений. Существуют разные методы нахождения этих коэффициентов (Hohendorf K.; 1966, Рикер У.Е., 1979; Барыбина А.И., 1978 и др.). Однако недостатком всех этих методов является то, что для определения неизвестных коэффициентов длина рыбы должна быть известна через равные интервалы времени. Если интервалы времени, для которых определена длина, не являются постоянными (то есть отсутствуют регулярные измерения), то для этих случаев известные методы не применимы. Целью данной работы является разработка методики определения коэффициентов уравнения линейного роста Берталанфи на основе экспериментальных измерений длины, проведенных через неравные интервалы времени. Если продифференцировать уравнение (1) и провести несложные преобразования, то можно получить следующее выражение для скорости роста рыбы: 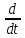 [l(t)] = KL − Kl(t) [l(t)] = KL − Kl(t). (2) где 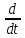 [l(t)]– скорость роста рыбы. [l(t)]– скорость роста рыбы.Из уравнения (1) видно, что скорость роста зависит от длины рыбы. Анализ показывает, что выражение (2) является уравнением линейной функции в декартовой системе координат, по оси абсцисс которой откладывают длину рыбы l(t) в некоторый момент времени t, а по оси ординат скорость роста рыбы 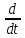 [l(t)] в этот момент. В момент времени tk, когда длина рыбы достигнет предельной длины l(tk) = L, скорость ее роста становится равной нулю. И наоборот, в момент времени t0, когда длина рыбы равна нулю, скорость ее роста максимальна и равна [l(t)] в этот момент. В момент времени tk, когда длина рыбы достигнет предельной длины l(tk) = L, скорость ее роста становится равной нулю. И наоборот, в момент времени t0, когда длина рыбы равна нулю, скорость ее роста максимальна и равна 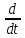 [l(t)]=KL. Это можно использовать для нахождения неизвестных коэффициентов уравнения Берталанфи. [l(t)]=KL. Это можно использовать для нахождения неизвестных коэффициентов уравнения Берталанфи.На рис. 1 изображены и отмечены кружками значения скорости роста рыбы в зависимости от длины, найденные на основе измерений длины в некоторые моменты времени t. В соответствии с выражением (2) значения скорости роста, могут быть аппроксимированы прямой линией, проходящей через эти точки. Аналитическое выражение этой прямой, позволяет найти неизвестные коэффициенты уравнений (2) и (1). 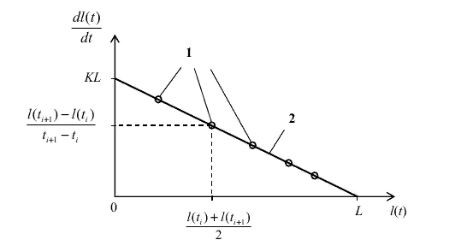 Рис. 1 Зависимость скорости роста рыбы от длины 1 – Значения скорости роста, найденные на основе измерений длины и возраста; 2 – Линейная зависимость в соответст- вии с уравнением (2) В соответствии с изложенным выше, определение коэффициентов уравнения роста Берталанфи можно проводить в следующей последовательности. 1). Для некоторых возрастов рыбы ti производят измерения ее длины l(ti). Количество измерений должно быть не менее трех. 2). Затем для нескольких последовательных пар значений изменения возраста находят среднею длину рыбы на j-ом интервале изменения возраста 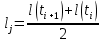 где lj – средняя длина рыбы на j-ом интервале изменения возраста; l(ti) и l(ti+1) – длина рыбы соответственно в возрасте ti и ti+1 ; 3). На каждом j-ом интервале изменения возраста рыбы определяют скорость ее роста: 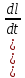 = = 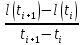 .(3) где j – интервал возраста, для которого определяется скорость роста; 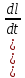 - скорость роста на j-ом интервале изменения возраста; - скорость роста на j-ом интервале изменения возраста;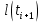 и и 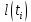 – длина рыбы соответственно в возрасте ti+1 и ti. – длина рыбы соответственно в возрасте ti+1 и ti.4). Строят таблицу, в которой приводят экспериментальные данные скорости роста рыбы на j-ом интервале изменения возраста и соответствующую этому интервалу среднюю длину. 5). Затем методом регрессионного анализа с использованием стандартных компьютерных программ, предназначенных для обработки статистических данных (например, Excel, Statistica или др.), находят аналитическое выражение уравнения прямой линии (у = аx + b), аппроксимирующей экспериментальные точки зависимости скорости роста от длины рыбы. Численные значения коэффициентов а и b найденного регрессионного уравнения, позволяют найти значения средней предельной длина рыбы L= 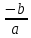 , ,и константу, характеризующей скорость изменения длины К = – а уравнения Берталанфи (1). 6). Нахождение коэффициента t0 уравнения Берталанфи (1) осуществляется в два этапа. а). Для каждого из измеренных значений длины рыбы l(ti), соответствующей возрасту tiи найденным коэффициентам К и L находим значение (t0)i по формуле 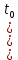 (4) б). Находим коэффициент t0 как среднее всех значений, рассчитанных по формуле (4). Таким образом, предлагаемая методика позволяет достаточно просто рассчитать коэффициенты уравнения роста Берталанфи по измеренным значениям длины рыбы и ее возрасте. Достоинством методики является то, что измерения длины не обязательно должны производиться через равные интервалы времени. Заключение Главной задачей сейчас является регулирование рыболовства. Считалось, что рыбные запасы в Мировом океане неисчерпаемы, и уменьшение численности или внезапные исчезновения некоторых видов рыб объяснялись их перемещениями в неведомые районы. Хотя вскоре выяснилось, что настоящей причиной оскудения является излишне усердный лов рыбы. Поэтому ради поддержания максимального уровня улова в районах рыбного промысла стали применяться международные меры по их сохранению. Проблемы регулирования рыболовства очень сложны. Подсчитать запасы рыбы, ракообразных и моллюсков чрезвычайно трудно. Многие виды рыб нерестятся в водах одних стран, а ловятся во время миграции через воды совсем других стран, при этом между первыми и вторыми договоренность о единообразии мер регулирования либо недостаточно четкая, либо вообще отсутствует. Мало что известно о многих факторах окружающей среды, от которых зависит воспроизводство рыбы, ее рост, миграция и замор. Даже определение допустимого улова некоторого конкретного вида рыбы требует долговременных и весьма трудоемких поисков решения чрезвычайно сложных задач. Количественным показателем развития рыб является их рост. Поэтому математическая оценка количественных параметров роста в естественных условиях имеет первостепенное значение при изучении динамики рыбных ресурсов и разработке мероприятий по их рациональному использованию. Литература 1. Калайда, М. Л. Методы рыбохозяйственных исследований: учебное пособие для студентоввузов./ М. Л. Калайда, Л. К. Говоркова. - СПб.: Проспект Науки, 2013. - 288 с. ISBN 978-5-903090-87-7. 2. Корпачев, В.С. Водные ресурсы и основы водного хозяйства./ В.С. Корпачев, И.А. Бабкна .- СПб.: Изд-во: Лань, 2012. – 384 с. ISBN 978-5-8114-1331-7. 3. [Электронный ресурс] -https://wikijaa.ru/wiki/Ludwig_von_Bertalanffy#cite_note-10 |
