Уравнение Клапейрона-Менделеева реферат. Уравнение КлапейронаМенделеева. Основное уравнение молекулярнокинетической теории идеальных газов
 Скачать 38.37 Kb. Скачать 38.37 Kb.
|
|
РЕФЕРАТ по дисциплине: Теплофизика на тему: Уравнение Клапейрона-Менделеева. Основное уравнение молекулярно-кинетической теории идеальных газов Выполнил: Студент___курса Заочной формы обучения (ФИО) Москва 2015 г. ОглавлениеВведение 3 1. От законов к уравнению 4 2. Идеальное соотношение для идеальных газов 7 3. Почему оно идеальное 8 Заключение 10 Список использованных источников 11 ВведениеСегодня ни физика, ни химия, ни любая другая естественная наука немыслима без этой универсалии – уравнения состояния идеального газа. В современной науке это уравнение носит название «уравнение Менделеева-Клапейрона». Действительно, оба ученых независимо друг от друга по сути вывели это уравнение из имеющихся на том этапе данных о свойствах идеальных газов. На практике идеальных газов не существует, как, наверное, не существует вообще ничего идеального. Однако многие газообразные вещества при определенных условиях проявляют свойства как бы идеальных газов. и весьма замечательно их состояние описывается известным не только великим умам современности, но и почти каждому школьнику уравнением. Цель реферативной работы – раскрыть сущность уравнения Менделеева-Клапейрона и оценить огромное значение этого нехитрого соотношения для современной науки. Задачами реферативной работы стали: - проведение исторического экскурса, - объяснение формулы, являющейся основой уравнения, - определение значимости уравнения для науки. При написании работы использовались труды самого Д.И. Менделеева, а также современных исследователей: Чугаева, Храмова, Дрофмана, Левченкова. 1. От законов к уравнениюК концу XVIII века наука встала на иной путь – путь непрерывного развития и совершенствования. Это происходит потому, что общество постепенно избавлялось от невежества и примитива, внушенных религиозным сознанием, и переходило от нелепых фантазий к исследованиям. Повсюду открываются научные школы, появляются первые труды ученых мужей, они публикуются без цензуры, вне страха перед кострами инквизиции. Мир познается не наощупь и не в религиозном бреду, а на основе наблюдений и размышлений. Конечно, предрассудки еще царствовали в умах даже тех, кто пытался перевернуть с ног на голову мировоззрение. Эти предрассудки тормозили научный прогресс, не давали смелым мыслям вырываться наружу. По-прежнему в ход пускалась фантазия, что-то домысливали, что-то оставляли на половине пути, так и не исследовав. Но механизм был запущен. Развитие науки было уже не остановить. К концу XVIII века были созданы все предпосылки для исследований в области газообразных веществ. Газы всегда интересовали ученых своей загадочностью: ведь это были весьма «непослушные» вещества, которые «не хотели», чтобы их исследовали. Ведь газ сначала надо было поймать, потом постараться удержать, не теряя ни молекулы. Тем не менее экспериментальная работа велась, и велась она уже с XVI века. Начало пути к известному уравнению открыл английский ученый Роберт Бойль. Удивительно, но этот человек, положивший начало многочисленным исследованием в области газов, был религиозен, и более того, он занимался миссионерской деятельностью. Трудно было представить в те времена человека, который бы с равным рвением утверждал, что Христос в теле поднялся на небо, и что «при постоянной температуре и массе газа произведение давления на его объем остается постоянным»[8]. А ведь именно так Бойль в 1662 году сформулировал свой знаменитый закон, который впоследствии был назван законом Бойля-Мариотта, поскольку четырнадцать лет спустя этот закон будет сформулирован французским физиком Эдмом Мариоттом. Поскольку ученые работали независимо друг от друга, а Эдм Мариотт ничего не знал об открытии своего коллеги из Англии, - то патент на открытие по праву принадлежит им обоим[2]. Если давление газа – существенный для газообразного вещества параметр – обозначить P, а не менее важный для газа параметр – объем обозначить V, то закон Бойля-Мариотта будет записан в виде формулы: 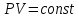 /1.1/ /1.1/Мариотт пошел дальше Бойля – он привел иную формулировку закона. Сначала он ввел понятие «состояние газа». Состояние газа – это набор определенных параметров: давления (P), объема (V) и температуры (T).Предположим, что газ перевели из состояния (1) в состояние (2) (сжали, расширили), сохраняя при этом постоянной температуру. Теперь газ будет характеризовать другими значениями давления и объема. Из состояния с давлением P1и объемом V1 он перешел в состояние с давлением P2 и объемом V2. При этом произведение PV не изменится. Учитывая соотношение /1.1/, можно записать: 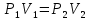 /1.2/ /1.2/Напишем это соотношение так: 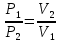 /1.3/ /1.3/Это соотношение и лежит в основе формулировки Мариотта: «Давление некоторой массы газа, находящегося при постоянной температуре, обратно пропорционально его объему». Закон Бойля-Мариотта действует исключительно в изотермических условиях. А как быть с теми условиями, когда, например, газ нагревается при постоянном давлении? На это вопрос ответил в начале, правда, уже XIXвека французский ученый Жозеф Луи Гей-Люссак. Он сформулировал закон, отражающий отношение между параметрами газа при постоянном давлении. Если давление постоянно, то при переходе газа из одного состояние в другое меняются лишь объем и температура. Гей-Люссак сформулировал этот закон как закон обратной пропорциональности между объемом и температурой газа при постоянном давлении. Если с формулировкой закона было вроде бы все ясно, то – вот парадокс! – совсем плохи дела обстояли с наименованием закона. Закон объемов (так назывался закон Гей-Люссака) впервые был опубликован в открытой печати в 1802 году Гей-Люссаком, однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году. Независимо от них закон был открыт в 1801 году английским физиком Джоном Дальтоном. Кроме того, качественно закон был описан французом Гийомом Амонтоном в конце XVII века. Пока ученые делили между собой славу открытия, закон уже вовсю работал на ниве теории идеальных газов. Математически его может выразить любой среднестатистический школьник: 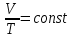 /1.4/, /1.4/, 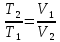 /1.5/ /1.5/Оставалось лишь понять, как объединить все три параметра: объем, давление, температуру. В 1811 году итальянец Амедео Авогадро на основе некоторых экспериментов показал, что «число молекул всегда одно и то же в одинаковых объемах любых газов». Эта формулировка стала законом Авогадро. За нее-то и зацепился Бенуа Поль ЭмильКлапейрон. И на основе объединения законов Бойля-Мариотта и Гей-Люссака, применяя закон Авогадро, он определил, что для данной порции любого газа отношение 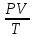 остается постоянным, даже если менять параметры[9]. остается постоянным, даже если менять параметры[9]. Итак, от законов, сформулированных для идеальных газов, был осуществлен переход к формуле. Закона Клапейрона существовать никогда не будет. Зато будет существовать формула, которая станет наиважнейшей формулой теории идеальных газов. 2. Идеальное соотношение для идеальных газовВеликое открытие в теории идеальных газов было сделано Клапейроном в 1834 году. Сорок лет спустя великий Менделеев не оставит это открытие без внимания. В 1874 году (уже после открытия Периодического Закона) Дмитрий Иванович определит, наконец, что же это за загадочная постоянная, держащая в узде три параметра газообразного вещества: объем, давление и температуру. В результате многочисленных опытов, Менделеев установит, что соотношение 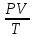 для одного моля любого газообразного вещества (1 моль – это примерно 6,023 * 1023 частиц) равно 8,314. Что это за величина? Оказывается, это есть не что иное, как работа расширения одного моля идеального газа в изобарном процессе (P = const) при увеличении температуры на 1 К. Эту величину Менделеев назвал универсальной газовой постоянной. И обозначил ееR. Теперь соотношение Клапейрона приобретало конкретный вид: для одного моля любого газообразного вещества (1 моль – это примерно 6,023 * 1023 частиц) равно 8,314. Что это за величина? Оказывается, это есть не что иное, как работа расширения одного моля идеального газа в изобарном процессе (P = const) при увеличении температуры на 1 К. Эту величину Менделеев назвал универсальной газовой постоянной. И обозначил ееR. Теперь соотношение Клапейрона приобретало конкретный вид: 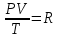 /1.6/. /1.6/.Но это – для одного моля газа. А если количество газообразного вещества больше или меньше? Знаменитый гений и здесь не замялся, и быстро ответил: «Ну… тогда универсальную газовую постоянную надо умножить на количество!»[10]. Теперь формула /1.6/ еще более конкретизируется:/1.7/, где 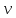 как раз то пресловутое количество газа, на которое предлагал умножить универсальную газовую постоянную Менделеев[7]. как раз то пресловутое количество газа, на которое предлагал умножить универсальную газовую постоянную Менделеев[7].Но количество вещества газа связана с его массой соотношением: 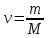 /1.8/. Объединяя соотношения /1.7/ и /1.8/, получим: /1.8/. Объединяя соотношения /1.7/ и /1.8/, получим: 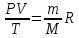 /1.9/. /1.9/.Уравнение /1.9/ и называется уравнением Менделеева-Клапейрона. Его другое название – уравнение состояние идеального газа. Оно настолько точно описывает поведение идеальных газов, что вправе получить эпитет «идеальное» уравнение. 3. Почему оно идеальноеНе надо быть великим математиком, чтобы понять, какие интересные величины можно вывести из уравнения состояния идеального газа. Во-первых, само уравнение позволяет найти любой параметр газа, если известны его масса и два других параметра. Если преобразовать уравнение, то можно найти много интересных величин. Например, плотность газа при определенных условиях. Плотность газа – это отношение массы газа к его объему, то есть ⍴ = 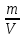 /1.10/. В уравнении /1.9/ можно эту плотность определить: /1.10/. В уравнении /1.9/ можно эту плотность определить:  ↔ ↔ . .Наконец, любому школьнику будет интересно знать, откуда же берется это число 22,4, о котором учитель химии на уроке все уши прожужжала. Чтобы вести расчеты с газами, необходимо хотя бы образно привести их к одинаковым условиям, иначе получится нелепица и чехарда. Обычно относят к так называемым «нормальным условиям», при которых давление P = 101,325 кПа, температура T = 273 К (0 градусов по шкале Цельсия). А 22,4 – это величина молярного объема – объема, который занимает 1 моль любого газа. Применяем наше идеальное уравнение  , только в виде , только в виде  , и первое, что видим, так это: , и первое, что видим, так это: 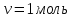 . . Подставляем единицу в формулу 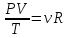 и получаем: и получаем:V = 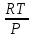 = = 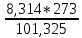 = 22,4 (л/моль). = 22,4 (л/моль). В объем данной работы не может войти всех областей применения идеального уравнения для идеальных газов. А их очень много! ЗаключениеТаким образом, уравнение состояния идеального газа отражает взаимосвязь между его параметрами и массой. Поскольку любой газ при достаточно низких давлениях ведет себя почти «идеально», то следует вывод, что уравнение Менделеева-Клапейрона универсально. Оно применимо и в области повышенных давлений, только с известными поправками. Уравнение Менделеева-Клапейрона с успехом применяется не только в теории газов, но и в термодинамике, теплотехнике. Его вездесущность трудно переоценить. Оно позволяет найти дополнительные величины, которыми характеризуется газообразное вещество. В заключение хочется привести известную фразу Дмитрия Ивановича Менделеева:«Наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры». Список использованных источниковВсеобщая история химии. Становление химии как науки / Отв. ред. Ю. И. Соловьев. — М.: Наука, 1983. — 464 с. Дорфман Я. Г. Всемирная история физики. С начала XIX до середины XX века. — Изд. 3-е. — М.: ЛКИ, 2011. — 317 с. Кудрявцев П. С. Курс истории физики. М. «Просвещение», 1982 Левченков С. И. Краткий очерк истории химии.. — Ростов-на-Дону: Изд-во Рост. ун-та, 2006. — 112 с. Менделеев Д. И. Еще о расширении жидкостей (Ответ профессору Авенариусу). — СПб.: Тип. В. Демакова, 1884. — 18 с. Менделеев Д. И. Об опытах над упругостью газов. Сообщение Д. И. Менделеева в Императорском Русском техническом обществе — 21 янв. 1881 г. — СПб., 1881. — 22 с. Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высш. шк., 2009. — 527 с. Храмов Ю. А. Бойль Роберт // Физики: Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. Храмов Ю. А. Клапейрон Бенуа Поль Эмиль (Clapeyron Benoit Paul Emile) // Физики: Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — С. 133. — 400 с ЧугаевЛ. А. Дмитрий Иванович Менделеев. Биография русского гения // Экология и жизнь. — 2009. — № 1. |
