Сулейманов_Башев_LR3_Rstudio. Введение в систему R
 Скачать 1.48 Mb. Скачать 1.48 Mb.
|
|
ФГБОУ ВО "Уфимский государственный авиационный технический университет" Кафедра вычислительной математики и кибернетики Расчетно-графическая работа по дисциплине “Интеллектуальный анализ данных” «Введение в систему R»
Уфа 2021 ОглавлениеЗадание №1 3 Выполнение задания 3 Вывод 6 Задание 2 7 Выполнение задания 7 Задание 3 10 Выполнение задания 10 Вывод 11 Задание 4 12 Выполнение задания 13 \Вывод 14 Задание №11) Сгенерируйте вектор длины N=1000, элементами которого являются реализации нормально распределенной случайной величины с математическим ожиданием, равным 1, и стандартным отклонением, равным 0.3. 2) Подсчитайте статистическое мат. ожидание и стандартную ошибку, не используя встроенные функции и проверьте правильность результата. 3) Подсчитайте .95, .99 - квантили. 4) Исследуйте отклонение статистического математического ожидания от 1 при росте N (N=1000,2000,4000,8000). Выполнение заданияСгенерируем вектор длины 1000 с помощью функции rnorm (n, mean, sd), которая возвращает вектор длины n=1000 со случайными элементами, распределенными по нормальному закону с математическим ожиданием mean=1 и стандартным отклонением sd=0.3 (см. ). 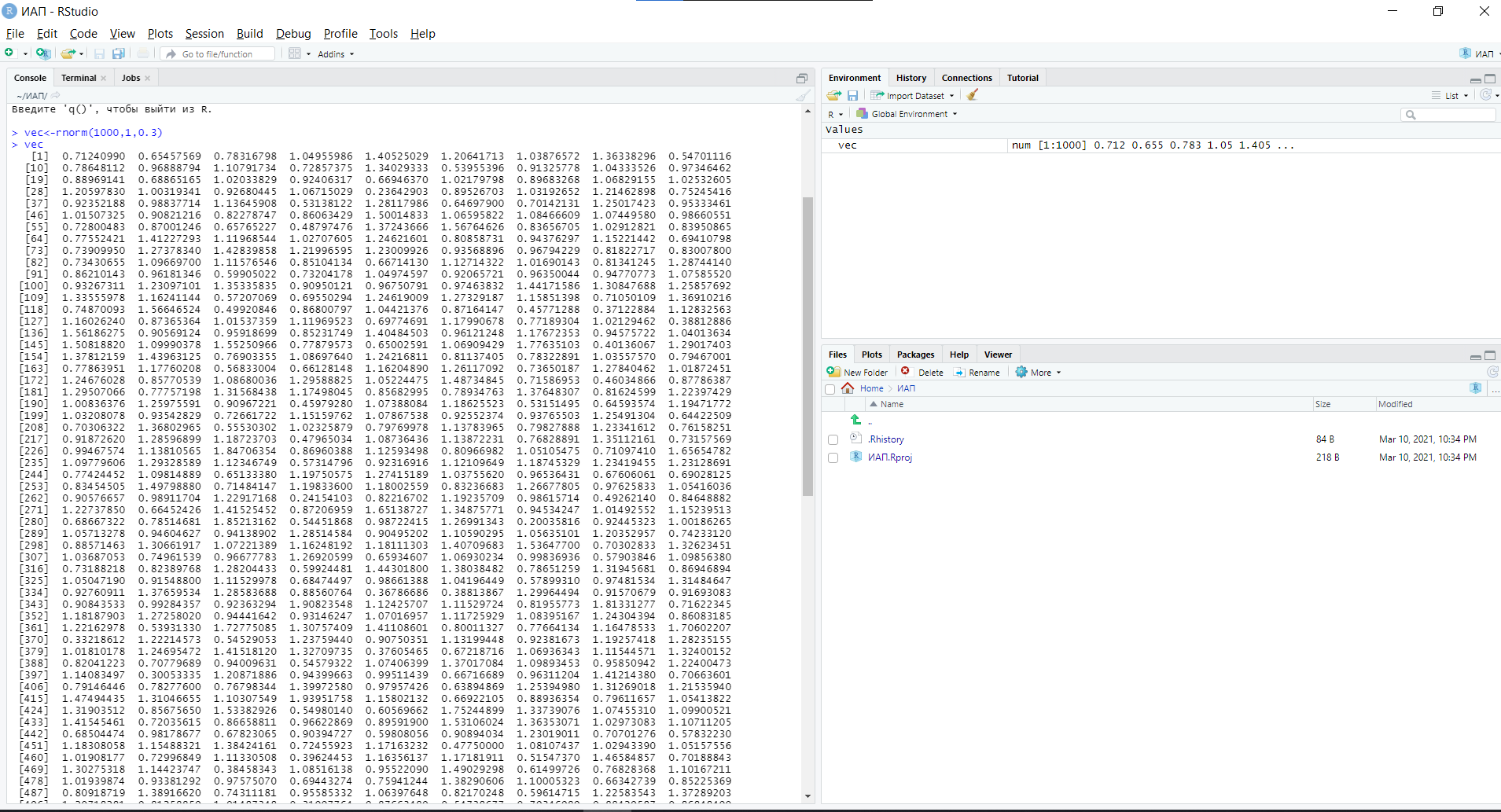 Рисунок 1 – Создание вектора с помощью функции rnorm(n, mean, sd) Посчитаем математическое ожидание, дисперсию, стандартное отклонение и написав функции math_o(x) и dispersion (x). Мат.ожидание - среднее (взвешенное по вероятностям возможных значений) значение случайной величины.[1] Математическое ожидание вычисляется, как сумма элементов вектора, поделенная на их количество. 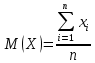 Стандартная ошибка среднего (или просто стандартная ошибка) приближенно показывает, насколько ее выборочная средняя(случайная наблюдаемая величина) отличается от среднего генеральной совокупности μ (фиксированная неизвестная величина). [1] Стандартное отклонение вычисляется как квадратный корень значения выборочной дисперсии: 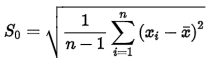 Реализация функции расчета математического ожидания: math_o <- function(x) { return(sum(x)/length(x)) } Реализация функции расчета стандартного отклонения: dispersion <- function(x) { mean = math_o(x) error = 0 for (i in x){ error = error + ( i - mean)^2 } error = error / (length(x) - 1) return(sqrt(error)) } Сравним результаты, полученные с помощью стандартных функций mean (математическое ожидание) и sd (стандартное отклонение) и с помощью собственных функций. Получены одинаковые результаты (см.Рис 2). 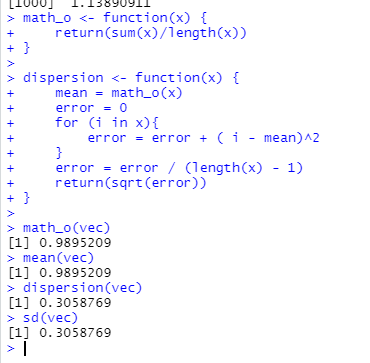 Рисунок 1–Проверка правильности результатов функций math_o(x) и dispersion (x) Подсчитаем 0,95-квантиль и 0,99-квантиль с помощью стандартной функции quantile(x, …) (см. Рис 3). Квантиль — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. [3]  Рисунок 2–Подсчет квантилей с помощью функции quantile(x, …) Исследуем отклонение математического ожидания вектора от 1 при его длине N, равной 1000, 2000, 4000 и 8000. Для этого создадим векторы указанной длины и посчитаем их математическое ожидание, стандартное отклонение и отклонение математического ожидания от 1. Сформируем фрейм данных из результатов (см. Рис4). 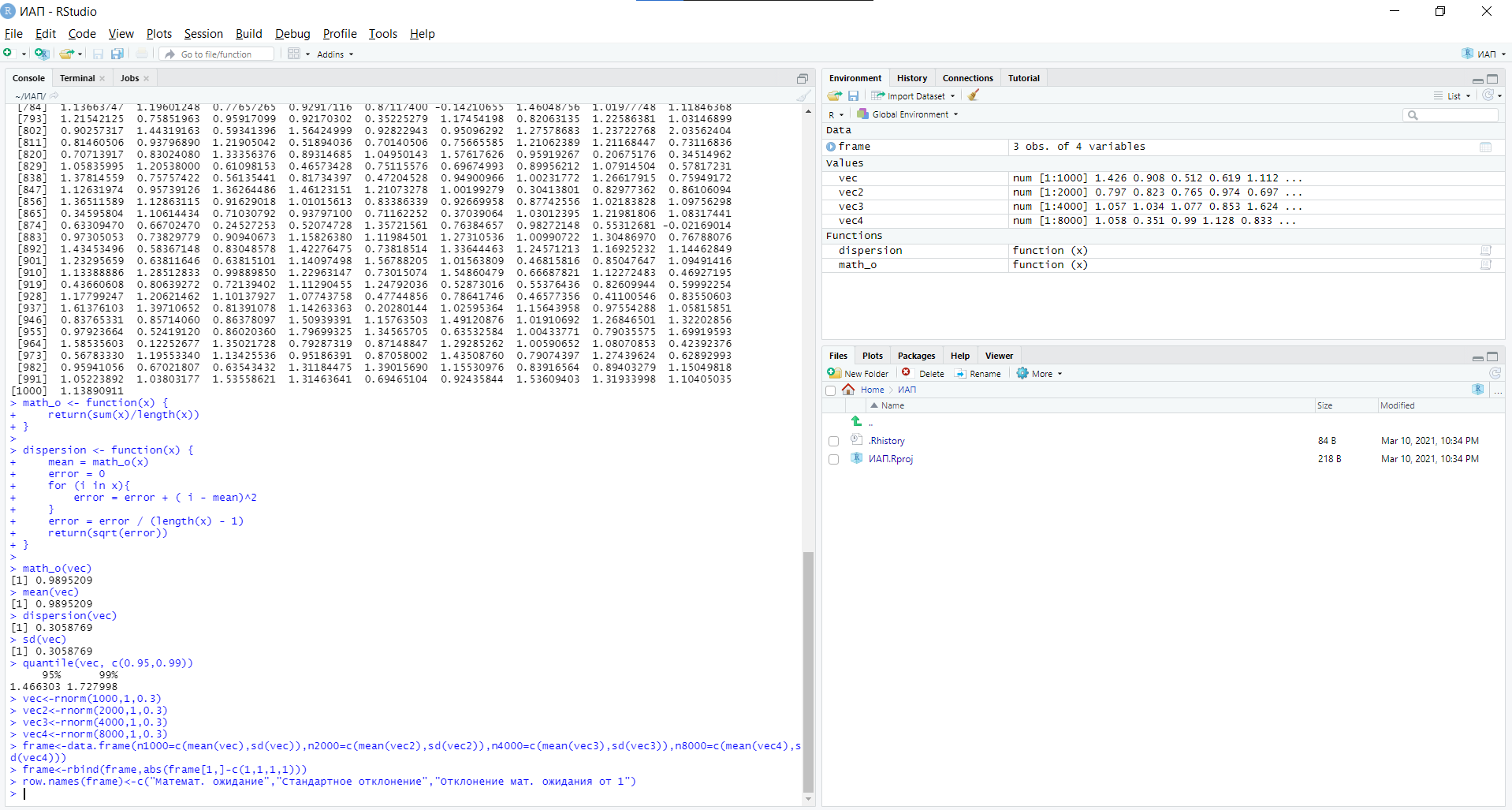 Рисунок 3–Подсчет математического ожидания при разных длинах векторов Построим график отклонения математического ожидания вектора от 1 при разных N (см Рис 5). 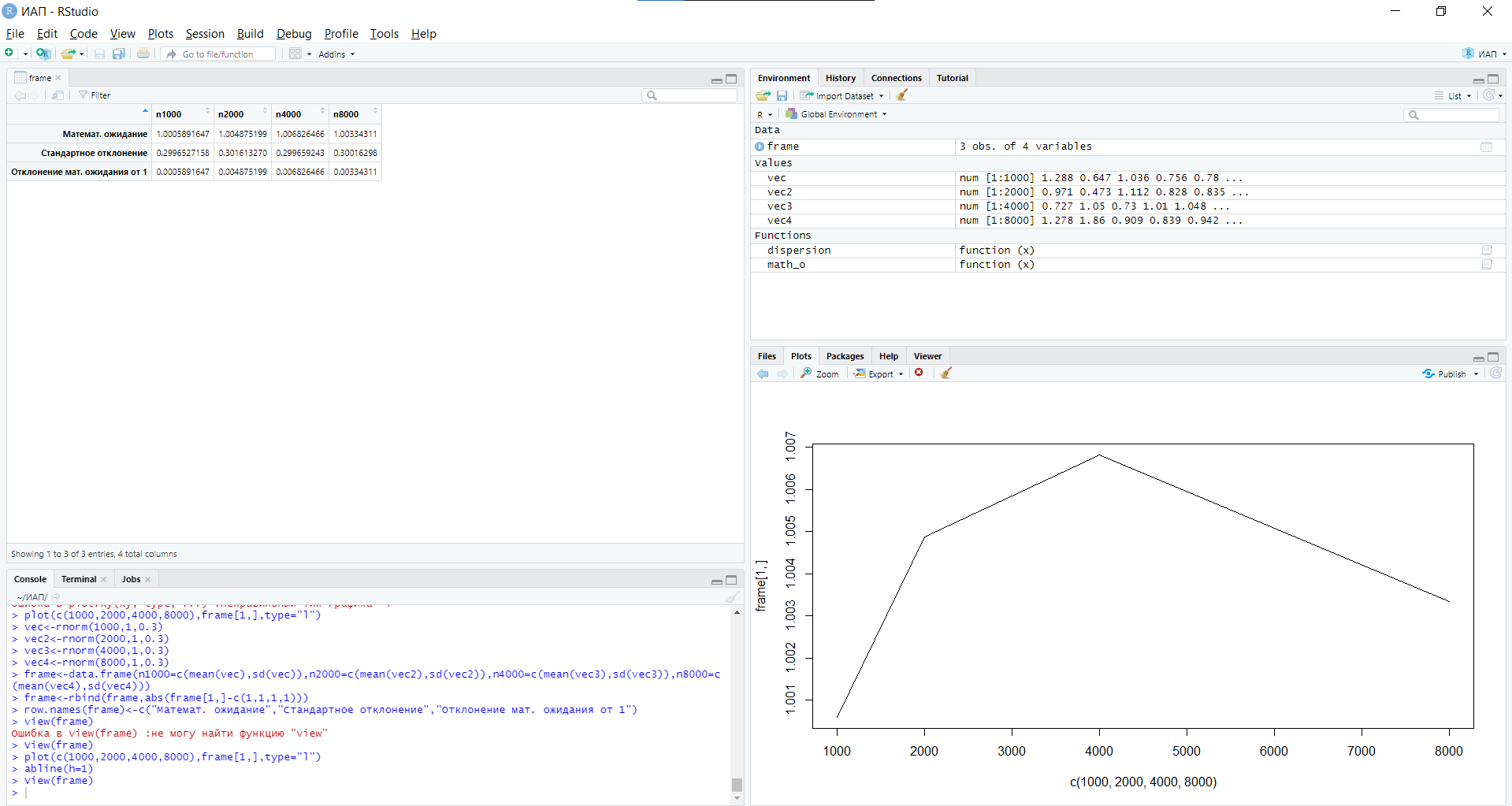 Рисунок 5– Построение графика отклонения математического ожидания вектора от 1 при разных N Вывод Как мы видим на графике, математическое ожидание векторов близко к единице, и при увеличении длины вектора, элементы которого распределены по нормальному закону с σ=0,3 и µ=1, отклонение статистического математического ожидания сначала стремится к 1.007, и после стремится к 0. Математическое ожидание колеблется около единицы, но амплитуда этих колебаний уменьшается. Задание 2 1)Создайте фрейм данных из N=20 записей со следующими полями: Nrow- номер записи, изменяется от 1 до N, Name - имя пользователя, задается произвольно, BithYear - год рождения, распределен равномерно на отрезке [1960,1985], EmployYear - год приема на работу, распределен равномерно на отрезке [BirthYear+18,2006], Salary -зарплата, для работников младше 1975 г.р. определяется по формуле Salary=(ln(2007-EmployYear) +1) *8000, ДляостальныхSalary=(log2(2007-EmployYear) +1) *8000. Вывести во фрейм 2) Добавьте в таблицу поле, соответствующее суммарному подоходному налогу (ставка 13%), выплаченному сотрудником за время работы в организации, если его зарплата за каждый код начислялась согласно формулам для Salary, где вместо 2007 следует последовательно подставить каждый год работы сотрудника в организации. 3) Подсчитайте число сотрудников с зарплатой, большей 15000. Выполнение задания Создадим вектор Ро, который содержит номер записи, изменяющийся от 1 до N. Создадим вектор Name с произвольными именами Name<-c("Олег","Влад","Боря","Маша","Игорь","Артур","Сулейман","Рустам","Настя", "Роман","Владимир","Булат","Аврора","Алиса","Александр","Метсола","Хартикайнен","Азамат","Ярослав","Кирилл") Cгенерируем вектор BirthYear<- sample(1960:1985, 20, replace=TRUE) год рождения, распределен равномерно на отрезке [1960,1985] Создадим вектор EmployYear - год приема на работу, распределен равномерно на отрезке [BirthYear+18,2006] EmployYear<- 1:20 for(x in 1:20){ EmployYear[x]<-sample((BirthYear[x]+18):2006,1) } Добавим вектор, содержащий количество отработанных лет каждого сотрудника work_exp <- 2007 -EmployYear Теперь рассчитаем salary(зарплату за последний год работы)и SalarySum(зарплату за все годы работы) для каждого сотрудника. Salary<- 1:20 SalarySum <- rep(0,20) for(x in 1:20) { if(BirthYear[x]<1975){ Salary[x] <-((log(work_exp[x])+1)*8000) for(i in 1:work_exp[x]) SalarySum[x] = SalarySum[x]+((log(i)+1)*8000)} else{ Salary[x] <- ((log2(work_exp[x])+1)*8000) for(i in 1:work_exp[x]) SalarySum[x] = SalarySum[x]+((log2(i)+1)*8000)} } Создадим фрейм с первичными данными (см. Рис 6) frameEmpl<- data.frame(Name,BirthYear,EmployYear,Salary,SalarySum) row.names(frameEmpl)<- Nrow colnames(frameEmpl) <- c("Name","BirthYear","EmployYear","Salary","SalarySum") 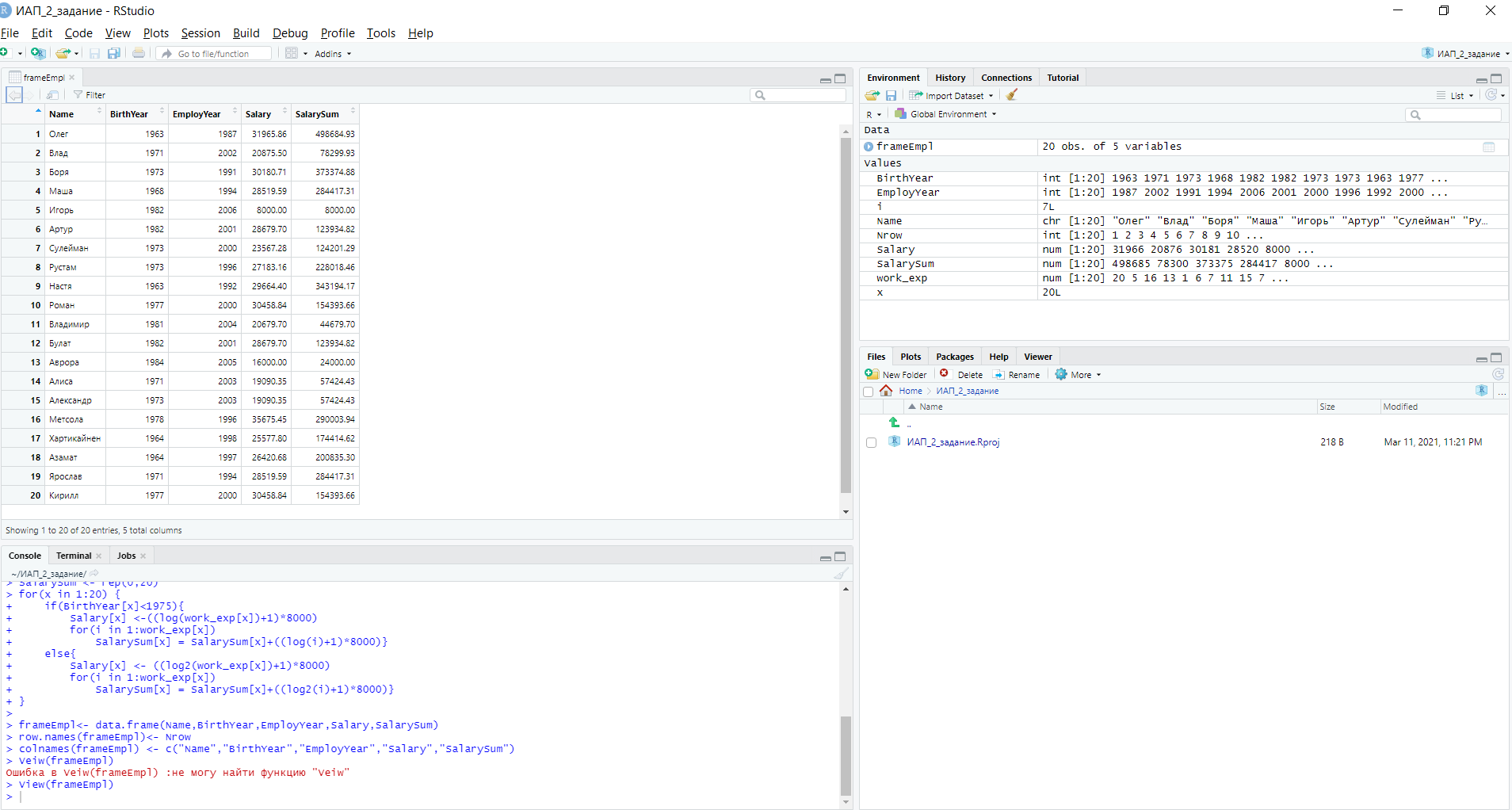 Рисунок 6– Вывод фрейма Создадим вектора, которые будут содержать подоходный налогTax за последний годи суммарный подоходный налог TaxSum за все годы работы: Tax <- c(0.13*Salary) TaxSum <- rep(0,20) for(x in 1:20) { for(i in 1:work_exp[x]){ if(BirthYear[x]<1975) TaxSum[x] = TaxSum[x] + ((log(i)+1)*8000*0.13) else TaxSum[x] = TaxSum[x] + ((log2(i)+1)*8000*0.13)} } Добавляем к старому фрейму новый столбец (см. Рис 7) frameEmpl <- cbind(frameEmpl,Tax=Tax,TaxSum=TaxSum) И выведем кол-во человек, у которых зарплата больше: 15000 print(paste("number of people with a salary more than 15000: ", length(Salary[Salary>15000]))) (см. Рис7) 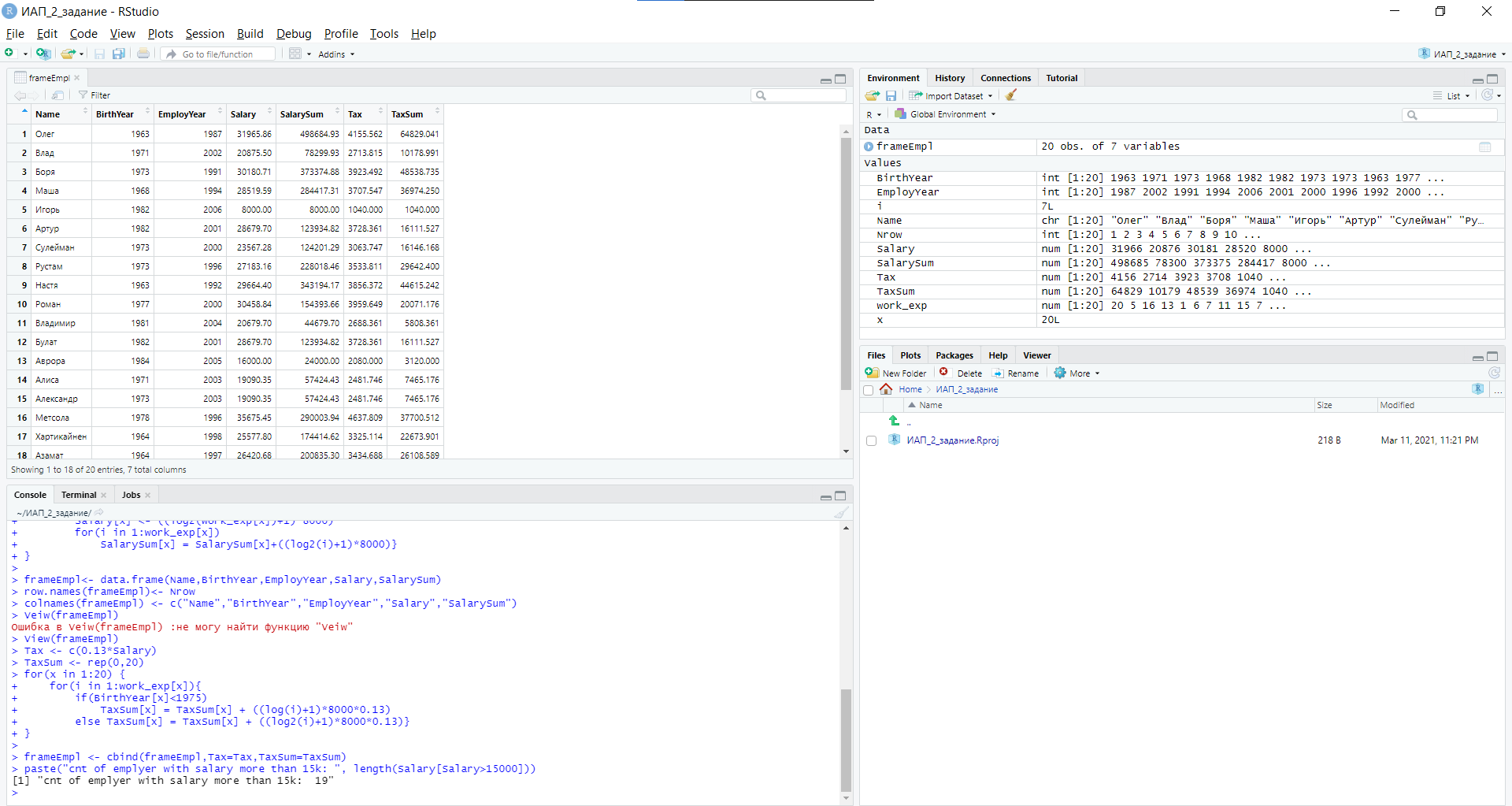 Рисунок 7– Вывод фрейма со столбцом налогов и количества человек с заработной платой менее 15000 Задание 3 Напишите функцию, которая принимает на вход числовой вектор x где x - вектор длины 5000, сгенерированный из экспоненциально распределенной случайной величины число разбиений интервала k. k=500 (по умолчанию равное числу элементов вектора, разделенному на 10) и выполняет следующее: находит минимальное и максимальное значение элементов вектора xmin и xmax, разделяет полученный отрезок [xmin;xmax] на k равных интервалов и подсчитывает число элементов вектора, принадлежащих каждому интервалу. Далее должен строиться график, где по оси абсцисс- середины интервалов, по оси ординат - число элементов вектора, принадлежащих интервалу, разделенное на общее число точек. Приближение какого графика мы получаем в итоге при большом числе точек и числе разбиений? Выполнение задания Реализуем функцию doPlot – которая находит количество значений в каждом из отрезков и функция middle_intervals, которая подсчитывает середины отрезков. Построим график с помощью встроенной функции plot(x,y), где х – вектор созданный с помощью функции rexp, у – вектор созданный с помощью функции middleIntervals. Ниже представлена реализация функций и построен график. (см. Рис 8) 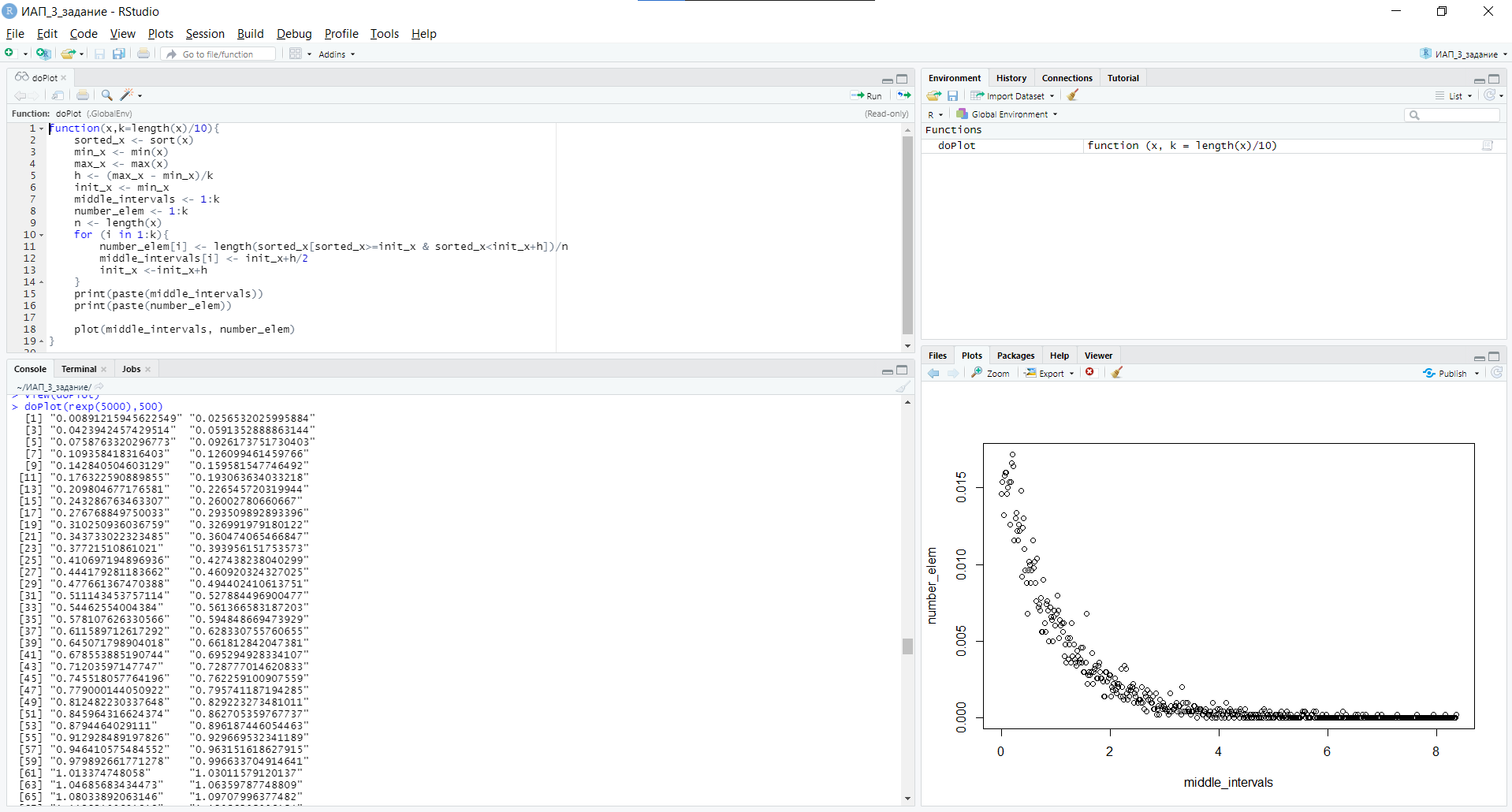 Рисунок8 – Результат вызова функции doPlot(x,500) Если построить график для вектора, состоящего из 50000 элементов, и k=1000, то график станет более похожим на график плотности вероятности экспоненциального распределения при λ=1 (см.Рис 9). 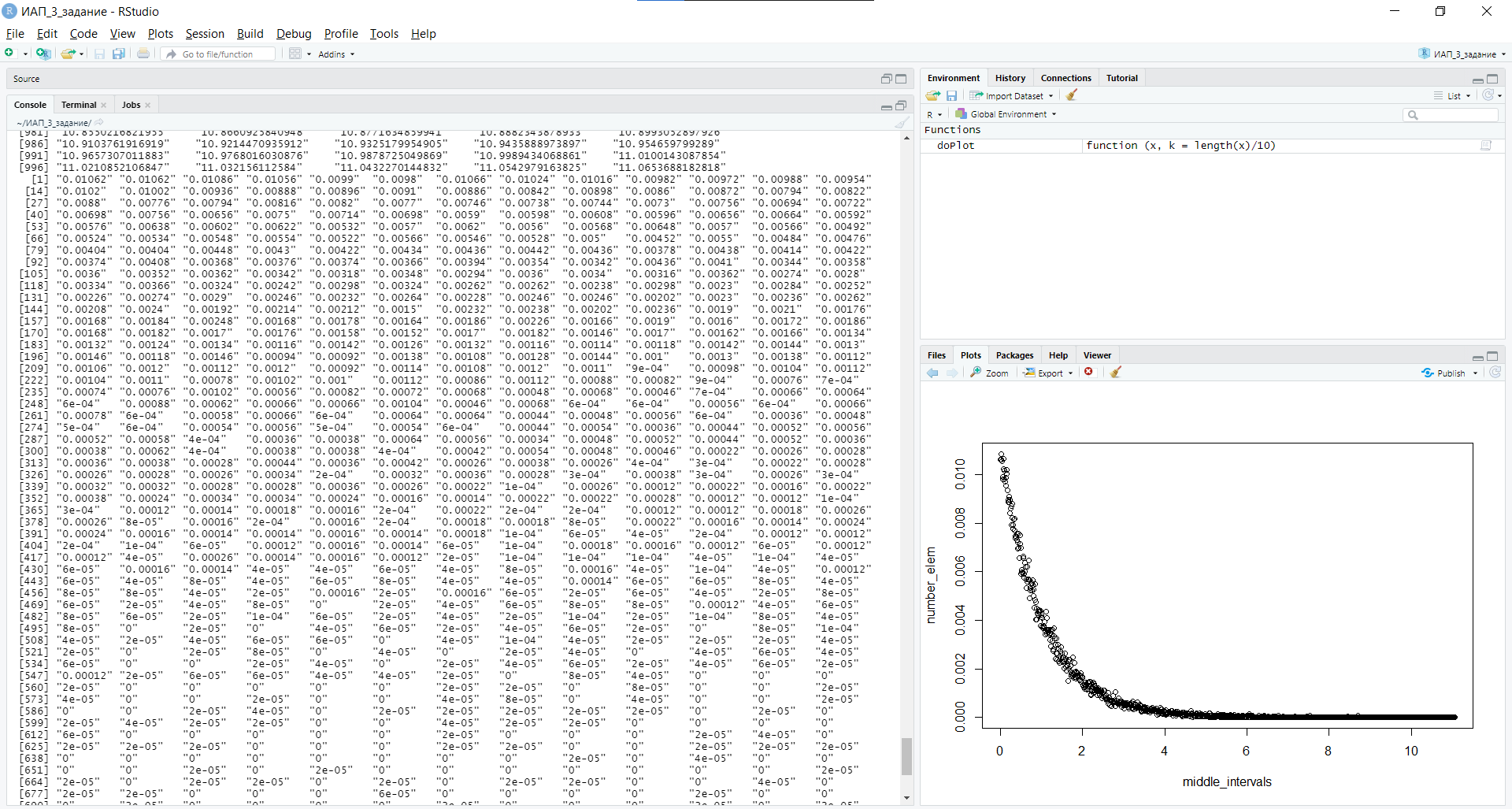 Рисунок 9– Результат вызова функции doPlot при n=50000 и k=1000 Вывод Наблюдая за графиком, можно сделать вывод, что это приближение графика плотности вероятности экспоненциального распределения. Задание 4 Спроектируйте и реализуйте метод наименьших квадратов. Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции.[2] Пусть имеются 2 вектора размерности N – x и у. Цель МНК найти Значения параметров 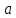 и и 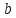 , при которых , при которых где n – число упорядоченных пар вокруг линии, максимально соответствующей данным. Для нахождения минимума функции необходимо найти её частные производные по переменным 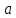 и и 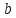 и приравнять их к нулю. А именно, решить систему уравнений относительно a и b чтобы найти исходные параметры. и приравнять их к нулю. А именно, решить систему уравнений относительно a и b чтобы найти исходные параметры.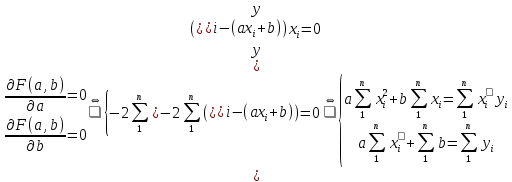 Решаем данную систему методом подстановки: 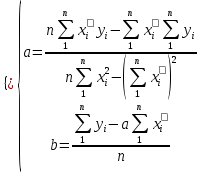 Таким образом, получаем следующую формулу: 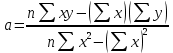  где xср — среднее значение x, независимой переменной, yср — среднее значение y, независимой переменной. Выполнение задания Напишем функцию, вычисляющую оценки коэффициентов 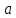 и и 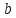 линейной зависимости линейной зависимости  по методу наименьших квадратов. по методу наименьших квадратов.Исходными данными являются мировые рекорды в тяжелой атлетике спортсменов разных весовых категорий: x – Вес спортсмена в кг y – Общий поднятый вес в кг (данные в рывковой и толчковой техниках)
Определим два вектора: x и y. Вычислим для них оценки коэффициентов с помощью функции MNK(x,y). Значения полученных коэффициентов a и b равны 2.81 и 157.12 соответственно (Error: Reference source not found 15). MNK 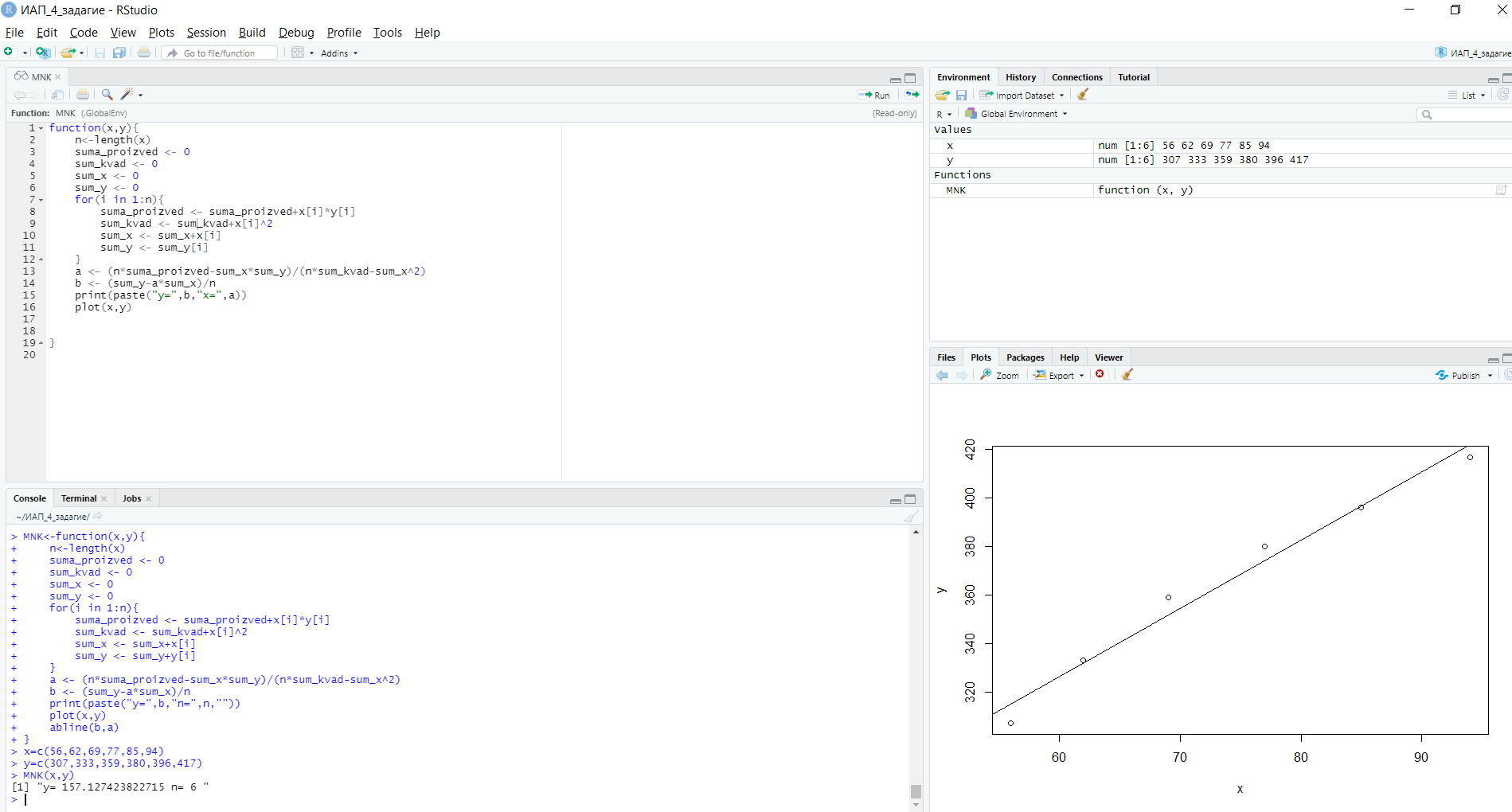 Рисунок 15–Работа функции MNK, построение графика функции \Вывод С помощью МНК была выявлена линейная зависимость, выраженная функцией y=2.81*x+157.12. С помощью этой функции можно судить о том, является ли суммарный вес, поднятый спортсменом, претендентом на мировой рекорд при весовой категории свыше 115 кг (115 кг - в олимпийских играх последняя весовая категория). Например, для спортсмена, весом 130 кг, претендующего на мировой рекорд, суммарный взятый вес должен быть примерно равен 522.5 кг. Ссылки на источники: http://mathprofi.ru/matematicheskoe_ozhidanie_i_dispersiya_nsv.html — теория для первого задания http://www.cleverstudents.ru/articles/mnk.html – метод наименьших квадратов Шмойлова Р. А., Минашкин В. Г., Садовникова Н. А. Практикум по теории статистики. — 3-е изд. — М.: Финансы и статистика, 2011. — С. 130—131. |
