Тема
|
Арифметический квадратный корень.
|
Тип урока
|
Урок изучения новых знаний
|
Цель
|
Знакомство с понятиями «квадратный корень» и «арифметический квадратный корень», формирование умения находить значение арифметического квадратного корня.
|
Планируемые
образовательные
результаты
|
Предметные: формирование понятий «квадратный корень» и «арифметический квадратный корень», умения находить значение квадратного корня.
Личностные: формирование интереса к новому учебному материалу, способам решения новых задач.
Метапредметные:
регулятивные - уметь ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку, работать по правилу, алгоритму и образцу, осуществлять оценку результата действия, логически мыслить, рассуждать, доказывать утверждения;
коммуникативные - умение слушать и вступать в диалог; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда, требовательное отношение к себе и своей работе;
познавательные - уметь читать математический текст и находить информацию в учебнике по заданной теме, на наглядно-интуитивном уровне проводить наблюдение, исследование, анализ и делать выводы.
|
Основные понятия
|
Квадратный корень, арифметический квадратный корень, знак корня (радикала), подкоренное выражение
|
Ресурсы
|
Учебник Алгебра. 8кл. Колягин, Ткачева и др.
|
Организация пространства
|
Фронтальная, индивидуальная.
|
Технология
проведения
|
Деятельность
учителя
|
Задания для учащихся, выполнение которых приведет к достижению запланированных результатов
|
Деятельность
учеников
|
Планируемые результаты
|
предметные
|
универсальные учебные действия (УУД)
|
I. Организационный момент.
Цели: создать деловой настрой для занятия; информировать о подготовке к уроку.
|
Приветствует учащихся, отмечает устно их готовность к проведению урока.
|
Концентрация внимания на необходимых действиях.
|
Слушают учителя, отвечают на вопросы.
|
Уметь сосредоточиться на определенном вопросе по математике.
|
Регулятивные:
уметь ориентироваться в требованиях к уроку математики.
|
II. Мотивация учебной деятельности.
Цели: выработка на лично значимом уровне положительного самоопределения ученика к деятельности на уроке.
|
Создает условия для формирования внутренней потребности учеников во включение в учебную деятельность.
Проговаривает девиз урока «Кто ничего не замечает, тот ничего не изучает. Кто ничего не изучает, тот вечно хнычет и скучает» (Ф. Сефа).
|
Концентрация внимания на девизе урока.
|
Слушают учителя, комментируют девиз.
|
Формирование представлений о математике как о методе познания окружающей действительности.
|
Личностные: Формирование мотивации к обучению и целенаправленной познавательной деятельности.
Регулятивные: Формирование умения самостоятельно определять цели своего обучения.
|
III. Актуализация опорных знаний.
Цели: актуализация изученных способов действий, достаточных для построения нового знания, их вербальная и знаковая фиксация и обобщение.
|
Предлагает заполнить таблицу значениями.
Задает вопросы.
|
На доске начерчена таблица (Приложение 1), такие же таблицы находятся на столах учеников.
Учитель предлагает заполнить таблицу значениями (необходимые вычисления выполняются на доске).
Задает вопросы:
- Какие задачи нам необходимо решить?
- О какой фигуре идет речь в V столбце? Как найти ее площадь?
- Составить уравнение по условию задачи: 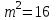 ( (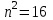 ). Решить его: ). Решить его: 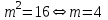 или или 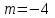 . Выбрать ответ, удовлетворяющий смыслу задачи: . Выбрать ответ, удовлетворяющий смыслу задачи: 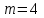 ; ; 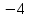 не удовлетворяет смыслу задачи, т. к. длина стороны выражается положительным числом. не удовлетворяет смыслу задачи, т. к. длина стороны выражается положительным числом.
|
Отвечают на вопросы, заполняют таблицу.
- Найти либо сторону, либо площадь прямоугольника. Проговаривают необходимые формулы, комментируют свои действия.
- Квадрат. Его площадь равна квадрату стороны.
- Составляют уравнение, подбирают корни. Дают объяснение, почему отрицательный корень не удовлетворяет смыслу задачи.
|
Уметь находить площадь прямоугольника и квадрата, длину стороны квадрата, если известна его площадь.
|
Регулятивные: организация своей учебной деятельности.
Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать, участвовать в коллективном обсуждении вопроса.
|
Открытие нового знания.
Цели: Сформировать понятие квадратный корень, понятие арифметический квадратный корень, научить читать выражения, содержащие квадратные корни.
|
Организовывает с учениками диалог.
|
Корни уравнения m2=16, т.е. числа, квадраты которых равны 16 называют квадратными корнями из числа 16.
Найдите определение квадратного корня в учебнике.
- Мы с вами узнали, что такое квадратный корень. Что же такое арифметический квадратный корень?
Найдите в учебнике определение арифметического квадратного корня.
Для обозначения арифметического квадратного корня ввели знак радикала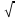
(лат. radex - корень).
Запись 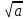 читают: квадратный корень из читают: квадратный корень из 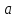 . .
Выражение, стоящее под знаком корня, называют подкоренным выражением.
Слово «арифметический» при чтении опускают.
Рассмотрим примеры нахождения арифметических квадратных корней:
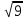 = 3, т.к. 32 = 9 и 3>0 = 3, т.к. 32 = 9 и 3>0
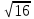 = 4, т.к. 42 = 16 и 4>0 = 4, т.к. 42 = 16 и 4>0
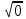 = 0, т.к. 02 = 9 и 0 – неотрицательное число. = 0, т.к. 02 = 9 и 0 – неотрицательное число.
Учитель подводит учащихся к определению арифметического квадратного корня в буквенном виде.
Учитель дает подсказку.
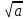 = =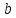 , если… , если…
Продолжите. Найдите формулировку в учебнике. Сравним с вашими предположениями.
Как вы думаете, всегда ли 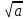 имеет смысл? (нет) Почему? (Т.к. квадрат любого числа неотрицателен). имеет смысл? (нет) Почему? (Т.к. квадрат любого числа неотрицателен).
Тогда при каких 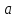 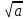 имеет смысл? имеет смысл?
(при 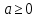 ). ).
Приведите примеры выражений, не имеющих смысл, запишите их в тетрадь.
Из определения арифметического квадратного корня следует:
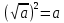 при при 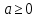 . .
Например,
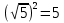
|
Принимают участие в диалоге. Работают с учебником. Слушают учителя, записывают в тетрадь обозначения и определения, проговаривают в парах определения.
|
Уметь извлекать квадратный корень, доказывать, что он извлечён верно.
|
Познавательные: уметь ориентироваться в необходимых формулах, использовать математический язык для оформления письменного решения примеров.
Коммуникативные: уметь слушать и понимать речь других, выражать мысли устно и письменно.
Регулятивные: уметь анализировать и делать выводы.
|
VI. Первичное применение нового знания.
Цели: научиться извлекать квадратные корни и объяснять ответ; определять, имеет ли смысл выражение с квадратными корнем.
|
Организует работу по решению примеров на доске и в тетрадях.
|
Решить задания учебника в тетрадях и на доске
№ 306 – 310 (нечётные).
|
Решают задания в тетрадях и на доске. Отвечают на вопросы учителя.
|
Уметь извлекать квадратный корень, доказывать, что он извлечён верно.
|
Познавательные: уметь ориентироваться в необходимых формулах, использовать математический язык для оформления письменного решения примеров.
Коммуникативные: уметь аргументировать своё мнение и позицию.
Регулятивные: уметь анализировать и делать выводы.
|
V.Рефлексия учебной деятельности.
Цели: зафиксировать содержание урока; организовать рефлексию и самооценку учениками собственной учебной деятельности.
|
Организует фиксирование изученного материала, рефлексию, самооценку учебной деятельности.
|
Ответить на вопросы:
Какое новое действие сегодня изучили?
Какое действие из известных самое сложное?
Что было непонятно?
|
Отвечают на вопросы учителя. Рассказывают, что повторили, узнали, смогли выполнить. Осуществляют самооценку.
|
Уметь повторять рассмотренные формулы, анализировать собственную учебную деятельность.
|
Регулятивные: уметь проговаривать последовательность действий на уроке, оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.
Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности
|
VI. Подведение итогов учебной деятельности, домашнее задание.
Цель: выставить оценки по итогам урока
|
Выставляет оценки с комментированием успешных и неуспешных действий учащихся
|
Домашнее задание: § 20. № 306 – 310 (чётные).
|
Слушают учителя, записывают домашнее задание, задают вопросы по необходимости
|
Уметь выявлять аналогию предметных действий.
|
Регулятивные: уметь прогнозировать ситуацию.
Личностные: уметь выполнять оценку и самооценку деятельности
|
 Скачать 36.17 Kb.
Скачать 36.17 Kb.
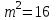 (
(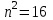 ). Решить его:
). Решить его: 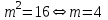 или
или 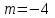 . Выбрать ответ, удовлетворяющий смыслу задачи:
. Выбрать ответ, удовлетворяющий смыслу задачи: 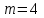 ;
; 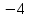 не удовлетворяет смыслу задачи, т. к. длина стороны выражается положительным числом.
не удовлетворяет смыслу задачи, т. к. длина стороны выражается положительным числом.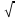
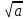 читают: квадратный корень из
читают: квадратный корень из 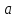 .
.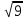 = 3, т.к. 32 = 9 и 3>0
= 3, т.к. 32 = 9 и 3>0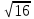 = 4, т.к. 42 = 16 и 4>0
= 4, т.к. 42 = 16 и 4>0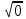 = 0, т.к. 02 = 9 и 0 – неотрицательное число.
= 0, т.к. 02 = 9 и 0 – неотрицательное число.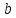 , если…
, если…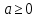 ).
).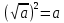 при
при