Математика. математика. Найти область определения функции, изобразить ее
 Скачать 43.82 Kb. Скачать 43.82 Kb.
|
|
Задание 1. Найти область определения функции  , изобразить ее. , изобразить ее.Подкоренное выражение должно быть неотрицательным и не может обращаться в ноль, получим строгое неравенство:    Уравнение 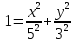 определяет эллипс, вершины эллипса находятся в точках определяет эллипс, вершины эллипса находятся в точках  которая делит координатную плоскость на две части – «внутренность» и «внешность» эллипса. которая делит координатную плоскость на две части – «внутренность» и «внешность» эллипса. Берем произвольную точку плоскости, например начало координат  , принадлежащую эллипсу , принадлежащую эллипсу 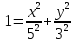 и подставим ее координаты в неравенство и подставим ее координаты в неравенство  : : получено верное неравенство, таким образом, точка получено верное неравенство, таким образом, точка  удовлетворяет неравенству удовлетворяет неравенству  как и любая точка, лежащая внутри эллипса. как и любая точка, лежащая внутри эллипса. Берем произвольную точку плоскости, например 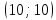 , не принадлежащую эллипсу , не принадлежащую эллипсу 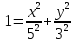 и подставим ее координаты в неравенство и подставим ее координаты в неравенство  : : получено неверное неравенство, таким образом, точка получено неверное неравенство, таким образом, точка 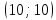 не удовлетворяет неравенству не удовлетворяет неравенству  как и любая точка, лежащая вне эллипса. как и любая точка, лежащая вне эллипса. Таким образом, искомая область определения внутренняя область эллипса 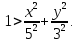 Задание 2. Найти частные производные 1-го порядка: 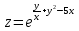   Задание 3. Найти полный дифференциал функции 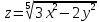 Полный дифференциал первого рода функции двух переменных имеет вид:     Задание 4. Дана функция  . Найти ее приближенное значение в т. . Найти ее приближенное значение в т. 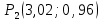 , исходя из ее точного значения в т. , исходя из ее точного значения в т.  . .Используем формулу    Вычислим значение функции в точке  : : Дифференциал функции в точке  найдем по формуле: найдем по формуле: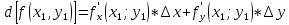 Вычисли частные производные 1-го порядка в точке  : :  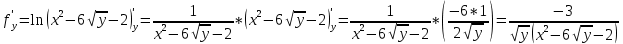 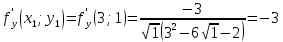 Полный дифференциал в точке 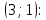 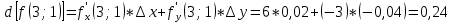 Таким образом по формуле  приближенное значение функции в точке приближенное значение функции в точке  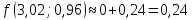 Задание 5. Показать что функция  удовлетворяет уравнению удовлетворяет уравнению 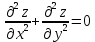 . .Найдем частные производные 1-го порядка:   Найдем частные производные 2-го порядка:   Подставим  и и 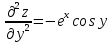 в левую часть уравнения в левую часть уравнения 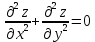  Получена правая часть данного уравнения, поэтому данная функция удовлетворяет данному уравнению Задание 6. Исследовать на экстремум функцию  . .Найдем частные производные 1-го порядка:   Получена система двух линейных уравнений с двумя неизвестными. 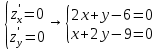 Из второго уравнения выразим  и подставим в первое уравнение: и подставим в первое уравнение:  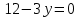   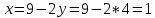  стационарная точка стационарная точкаПроверка: 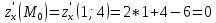 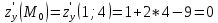 Применим достаточное условие экстремума функции двух переменных Найдем частные производные 2-го порядка в точке     Обозначим  Частные производные 2-го порядка равны константам, значит соответствующим константам они равны и в точке  : :   Тогда:  Следовательно в точке  есть экстремум, т.к. есть экстремум, т.к.  , то это минимум: , то это минимум: 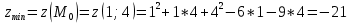 |
