Касательная к окружности. 1.Касательная к окружности_. Урок изучения нового Касательная к окружности, ее свойство и признак
 Скачать 1.1 Mb.
|
|
Урок изучения нового: Касательная к окружности, ее свойство и признак Учебная задача: • Ввести понятие касательной к окружности и точки касания. • Сформулировать и доказать свойство касательной и ее признак, показать их применение при решении задач. Диагностические цели урока: Учащиеся должны знать: определение касательной к окружности, точки касания; Учащиеся должны уметь: Формулировать и доказывать теорему о свойстве касательной к окружности и ее признак; Развивающая: развивать логическое мышление; умения применять знания в нестандартных ситуациях. Воспитательная: воспитывать аккуратность, культуру геометрической речи. Метод обучения: Объяснительно-иллюстративный Средства обучения: Доска, мел, рисунки, текст теста. Форма работы: Беседа. Структура урока: Повторение изученного ранее – 5 мин. Актуализация знаний учащихся – 3 мин. Мотивация учебной деятельности – 2 мин. Постановка целей и учебных задач – 3 мин. Сообщение темы урока – 2 мин. Ознакомление с новым материалом – 25 мин. Подведение итога урока и постановка домашнего задания –5 мин. Ход урока I. Мотивационно-ориентировочная часть Актуализация знаний учащихся Два ученика готовят решение домашних задач на доске, пока остальные учащиеся решают тест. Задания теста в распечатанном виде раздать на каждую парту. Проверка домашнего задания Проверить домашние задачи № 632, 633. Задача № 632 Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любая прямая, проходящая через точку А, является секущей по отношению к данной окружности. К 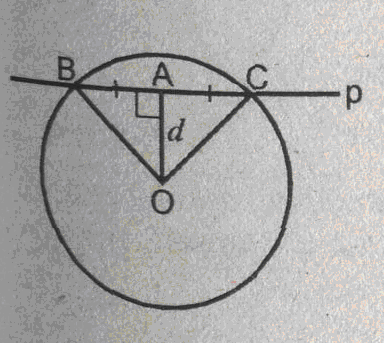 раткое решение (см. рис.):Пусть р произвольная прямая и на ней отложим два отрезка ABи АС такие, что AB=AC=  . По теореме Пифагора ОВ = ОС = обе точки В и С лежат на окружности, значит, прямая р является секущей по отношению к данной окружности. Задача № 633 Даны квадрат ОАВС, сторона которого равна 6 см, и окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности? К 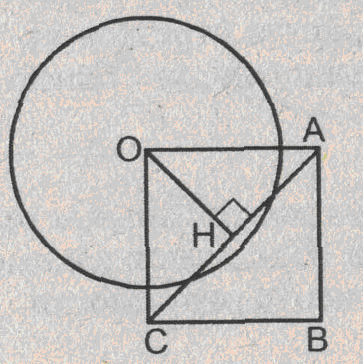 раткое решение (см. рис.):∆АСО - прямоугольный, так как ОАВС- квадрат. По теореме Пифагора АС2 = АО2 + ОС2 = 62 + 62 = 72 => АС = 6  см.ОН - высота равнобедренного треугольника АСО, проведенная к его основанию => ОН- медиана этого треугольника, то есть AH=HC=3 см.В ∆АОHпотеореме Пифагора ОН2= ОА2 - АН2= 62 –(3 )2 = 18 =>OH = 3 см  4,2 см.Радиус окружности равен 5 см => OH < r =>AC и окружность пересекается в двух точках. Итак, секущими по отношению к этой окружности, являются АС и ОА. АВ и ВС неявляются секущими, так как d=ОА = ОС = 6 см > r = 5 см. Ответ: АС и О А. Мотивация. Тест с целью проверки теории 1. Среди следующих утверждений укажите истинные. Окружность и прямая имеют две общие точки, если: а) расстояние от центра окружности до прямой не превосходит радиуса окружности; б) расстояние от центра окружности до прямой меньше радиуса окружности; в) расстояние от окружности до прямой меньше радиуса. Верный ответ: 2. 2. Среди следующих утверждений укажите истинные: а) Прямая а является секущей по отношению к окружности, если она имеет с окружностью общие точки. б) Прямая а является секущей по отношению к окружности, если она пересекает окружность в двух точках. в) Прямая а является секущей по отношению к окружности, если расстояние от центра окружности до данной прямой не больше радиуса. Верный ответ: б – истинно. 3. Закончите фразу, чтобы получилось верное высказывание. Окружность и прямая не имеют общих точек, если... Верный ответ: если расстояние от центра окружности до прямой больше радиуса окружности 4. Закончите фразу, чтобы получилось верное высказывание. Окружность и прямая имеют одну общую точку, если... Верный ответ: если расстояние от центра окружности до прямой равно радиусу окружности 5. Вставьте пропущенные слова. Окружность и прямая имеют одну общую точку, если расстояние от ... до прямой ... Верный ответ: ….центра окружности …. равно радиусу окружности Постановка учебной задачи: Мы познакомились с тремя видами взаимного расположения прямой и окружности и знаем как называется прямая, имеющая с окружностью две общие точки – это секущая. А сегодня мы познакомимся с определением прямой, имеющей с окружностью одну общую точку, узнаем ее свойства и признаки. II. Содержательная часть. 1 . Введение определения касательной и точки касания. Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Р 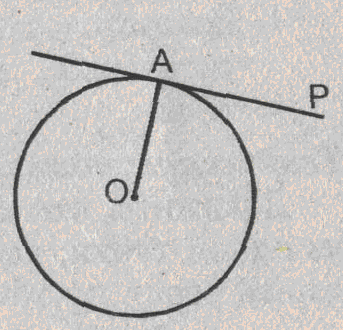 исунок и записи на доске и в тетрадях учащихся (см. рис.): р -касательная к окружности; А - точка касания.2. Доказательство теоремы о свойстве касательной к окружности лучше провести в ходе беседы учителя с учащимися по рис., приготовленному на доске. Теорема: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. - Предположим, что прямая р не перпендикулярна радиусу ОА. Сравните расстояние от центра окружности до прямой р с радиусом окружности. (Расстояние от точки О — центра окружности - до прямой р меньше радиуса, так как радиус ОА в данном случае является наклонной по отношению к прямой р, а расстояние от точки О до прямой р - перпендикуляром к прямой р, а как известно, любая наклонная больше перпендикуляра, проведенного из той же точки к той же прямой что и наклонная.) - Каково взаимное расположение прямой р и окружности? Почему? - Может ли прямая р быть касательной к окружности? Объясни. (Прямая р не может быть касательной к окружности, так как она имеет с ней две общие точки.) - Верно ли предположение, что прямая р не перпендикулярна радиусу ОА? О чем это говорит? (Предположение о том, что прямая р не перпендикулярна радиусу неверное, следовательно прямая р перпендикулярна радиусу.) 3. Ввести отрезки касательных, проведенные к окружности радиусом 9 см. Найдите длины отрезков ас и ао, если ав = 12 см">понятие отрезков касательных, проведенных из одной точки. Определение: Отрезки АВ и АС называются отрезками касательных, проведенных из точки А, если прямые АВ и АС являются касательными к окружности, точки В и С - точками касания. Р 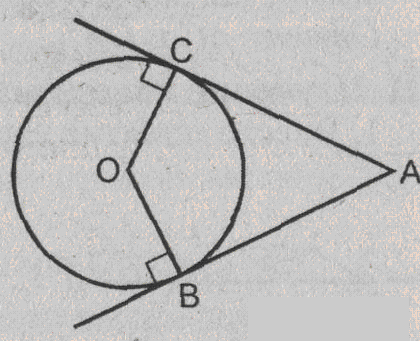 исунок и записи на доске и в тетрадях учащихся (см. рис.):АВ и АС — отрезки касательных, проведенных из точки А. В и С- точки касания. 4. Доказательство свойства отрезков касательных, проведенных из одной точки. Творческое задание: Докажите, что отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Для выполнения творческого задания дать учащимся 3-5 минут, а затем обсудить различные варианты решений. Если учащиеся не смогли самостоятельно справится с заданием, выполнить задание, используя наводящие вопросы. Решение (см. рис.): П 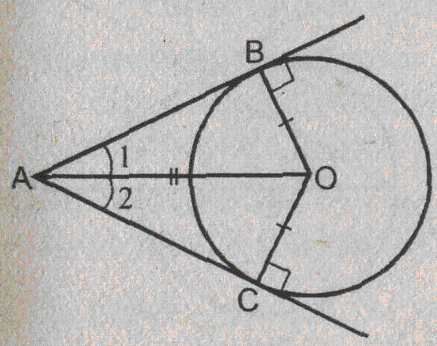 о теореме о свойствах касательной к окружности АВ  ОВ и АС ОС => ∆АОВ и ∆АОС - прямоугольные, они равны по катету (ОВ = ОС) и гипотенузе (ОА) =>АВ = АС и  1 = 2. Наводящие вопросы: - Соединим точки А и О отрезком. Что вы можете сказать о треугольниках АОВ и АОС? - Чем является луч АО для угла ВАС?О чем это говорит? 5. Знакомство с признаком касательной и его доказательство. - Сформулируйте теорему, обратную свойству касательной к окружности. Теорема: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. - Верна ли теорема, обратная свойству касательной к окружности? - Докажите ее справедливость. (По условию теоремы радиус является перпендикуляром к прямой, значит, расстояние от центра окружности до прямой равно радиусу. Это говорит о том, что прямая и окружность имеют одну общую точку, т.е. прямая является касательной к окружности.) 6. Решение задачи на построение. Д 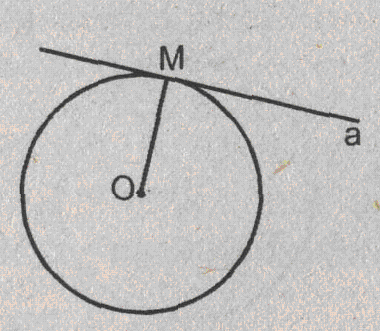 ана окружность с центром в точке О и точка М на ней. Построить касательную к окружности, проходящую через точку М (см. рис.). Вопросы для обсуждения: - Предположим, а — касательная к окружности, проходящая через точку М. Каково взаимное расположение прямой а и радиуса ОМ? - Как построить касательную к окружности, проходящую через М? IV. Закрепление изученного материала Разобрать решение задачи № 638. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если ОА=2см, а r = 1,5 см. Р 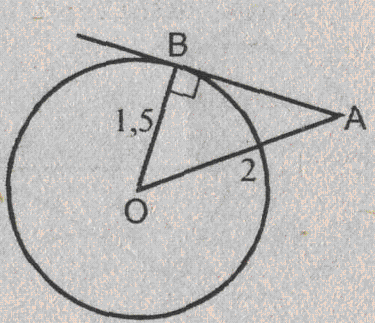 ешение (см. рис.):∆АОВ - прямоугольный, по теореме Пифагора АВ =  (см).Ответ:  см. Наводящие вопросы: - Как построить касательную к окружности? (Сначала провести радиус ОВ, где В - точка касания, затем провести прямую АВ так, что АВ ОВ.)- Докажите, что прямая АВ является касательной к окружности. (По признаку касательной к окружности.) 2. Решить самостоятельно задачи № 640, 635, 637. Задача № 640 Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательные к окружности. Найдите угол между ними, если ОА = 9 см К 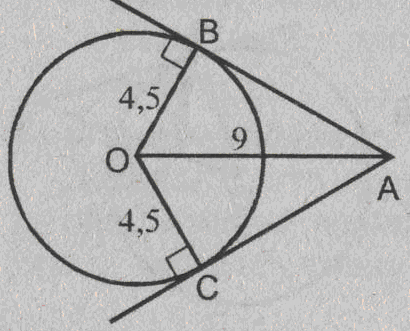 раткое решение (см. рис.):∆АОВ прямоугольный, ОА = 9 см, ОВ = 4,5 см => ВАО = 30°.∆ОАС = ∆АОВ => ОАС = 30° => ВАС = 60°. Ответ: 60°. Задача № 635 Через точку А окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними. 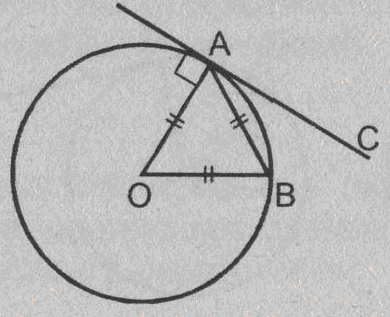 Краткое решение (см. рис.): В ∆АОВ ОА = АВ по условию задачи, ОВ = ОА как радиусы одной окружности => ∆АОВ - равносторонний, ОАВ = 60°.ОА АС => САВ = 90° - 60° = 30°. Ответ: 30°.Задача №637 Угол между диаметром АВ и хордой АС равен 30°. Через точку С проведена касательная, пересекающая прямую АВ в точке В. Докажите, что треугольник АСО равнобедренный. К 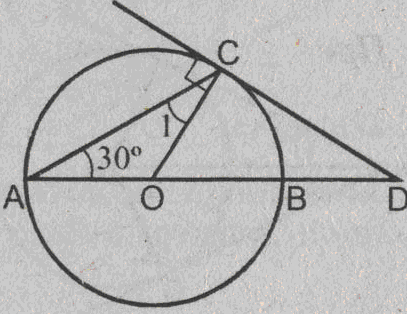 раткое решение (см.рис.):∆АОС - равнобедренный (ОА = ОС как радиусы) => 1= 30°, ОС СD(радиус окружности перпендикулярен касательной) => ОСD = 90°. АСD = 1+ ОСD = 180° - ( А + АСD) = 180° - (30° + 120°) = 30° => ∆АСD - равнобедренный с основанием АD.Дополнительная задача АВ и ВС - отрезки касательных, проведенных из точки В к окружности с центром О. Найдите АВ и ВС, если ОА = 16 см, а радиусы, проведенные к точкам касания, взаимно перпендикулярны. Р 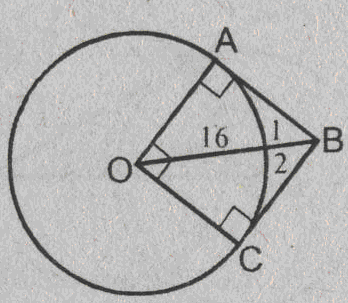 ешение (см. рис.):Т. к. ВА и ВС - отрезки касательных, проведенных из одной точки к окружности, то ОА АВ, ОС СВ, АВ = ВС и 1= 2 => AОВ = СОВ.Т. к. ОА ОС и AОВ = СОВ = 45° => 1=45°, 2 = 45°.∆АОВ - равнобедренный с основанием ОВ, значит, ОА = АВ. По теореме Пифагора ОА2 + АВ2 = ОВ2=> так как ОА = АВ, то 2 ОА2=162=>ОA = 8 см => АВ = BС= 8 см. Ответ: 8 см, 88 см. V. Подведение итогов урока Домашнее задание П. 69, вопросы 3-7; Решить задачи № 634, 636, 639 учебника. • Рассмотреть свойство отрезков касательных, проведенных из одной точки и показать его применение в процессе решения задач. Урок: Касательная к окружности. Решение задач Цели урока: • Закрепить теоретический материал п. 69. • Совершенствовать навыки решения задач по теме. Ход урока I. Организационный момент Сообщить тему урока, сформулировать цели урока. П. Актуализация знаний учащихся Теоретический опрос (Три ученика готовятся у доски.) - Сформулируйте и докажите теорему о свойстве касательной. - Сформулируйте и докажите теорему о свойстве отрезков касательных к окружности, проведенных из одной точки. - Сформулируйте и докажите теорему, обратную теореме о свойстве касательной. Проверка домашнего задания Проверить домашнюю задачу № 639 через графопроектор. Задачам 639 Прямая АВ касается окружности с центром О радиуса rв точке В. Найдите АВ, если А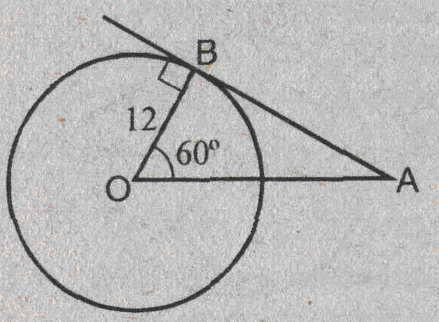ОВ = 60°, а r = 12 см.Р  ешение (см. рис.): ∆АОВ- прямоугольный, А = 90° - О = 30° =>ОВ =  ОА => ОА = 24 см.По теореме Пифагора АВ =  (см).Ответ:  (см). Наводящие вопросы - Каково взаимное расположение касательной АВ и радиуса ОВ. - Как найти катет АВ треугольника АОВ? Далее можно заслушать учащихся, подготовивших у доски доказательства теорем. Решение задач на готовых чертежах (Самостоятельно с последующей проверкой по готовым ответам.) Р 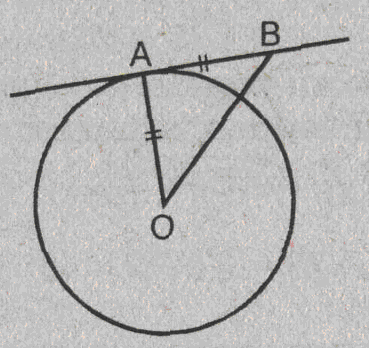 ис. Дано: К = 5, АВ- касательная. Найти: ОВ. ОТВЕТ: OB=  Р 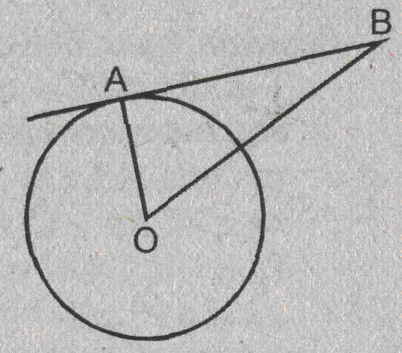 ис. Дано: АВ - касательная; АВ = 12, ОВ = 13. Найти: Rокружности. ОТВЕТ: R = 5. 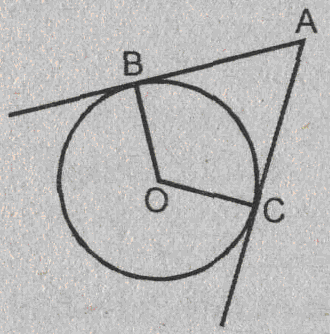 Рис. Дано: АВ, ВС - касательные, ОВ = 2, АО = 4. Найти: 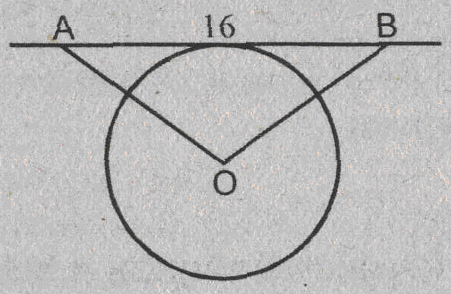ВОС.ОТВЕТ: ВОС=120  Рис. Дано: АВ - касательная, R = 6, АО = ОВ. Найти: АО. ОТВЕТ: АО=10. 5 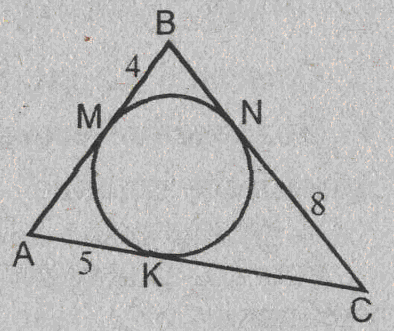 . Рис. Дано: М, М, К -точка касания. Найти: PABC. ОТВЕТ: PABC= 34. 6 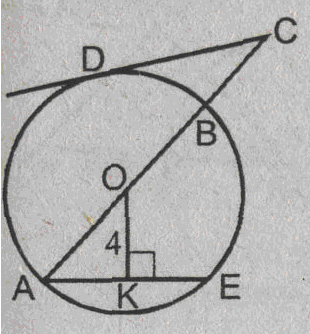 . Рис. Дано: АВ = 10 см, О - центр окружности, СD - касательная, АЕ || СD. Найти: ОС.ОТВЕТ: ОС =  .III. Решение задач 1. Самостоятельно решить задачи № 641, 644, 647, записав краткое решение (учитель в это время оказывает индивидуальную помощь менее подготовленным учащимся). Задача № 641 Отрезки АВ и АС являются отрезками касательных к окружности с центром О, проведенными из точки А. Найдите угол ВАС, если середина отрезка АО лежит на окружности. К 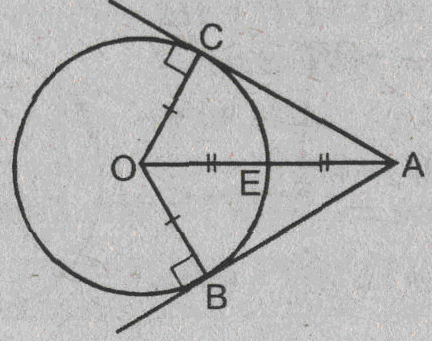 раткое решение (см. рис.):В ∆ОАС С = 90°, ОС = ОА => ОАС = 30° => ВАС= 60°.Задача № 644 Прямые МА и МВ касаются окружности с центром О в точках А и В. Точка С симметрична точке О относительно точки В. Докажите, что 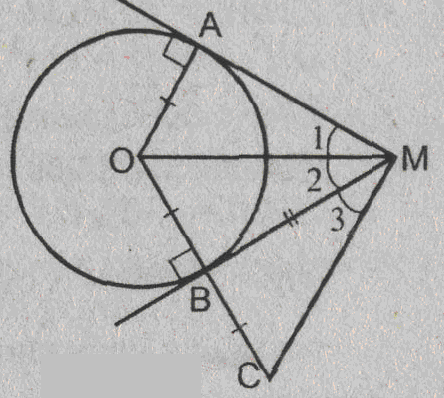АМС =3 ВМС.К  раткое решение (см. рис.):МА и МВ - отрезки касательных, проведенных из точки М => 1= 2. Точки О и С симметричны относительно точки В => ОВ = ВС и О, В, С лежат на одной прямой => ∆OMB = ∆СМВ по двум катетам => 2= 3=> АМС = 3 ВМС.Задача № 647 Отрезок АН — перпендикуляр, проведенный из точки А к прямой, проходящей через центр О окружности радиуса 3 см. Является ли прямая АН касательной к окружности, если: а) ОА= 5 см, АН = 4 см; б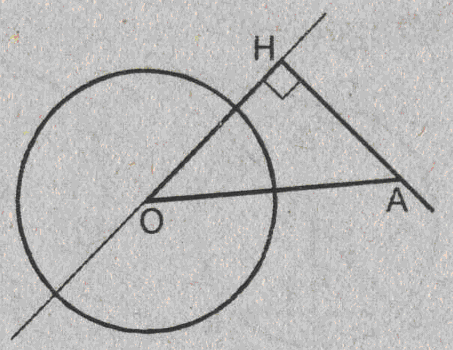) НАО = 45°, ОА= 4 см; в) НАО= 30°, ОА= 6 см?К  раткое решение (см. рис.): а) ОА = 5 см, АН = 4 см => ОН =  = 3 см = r=> АН - касательная к окружности. б) HОA = 45°, ОА = 4 см => ОН = НА, ОН2 + НА2 = ОА2=>2 ОН2 = 16 => ОН =  см  3 см => АН является касательной к окружности.в) HОA = 30°, ОА = 6 см =>OH = OA = 3 см = r=> АН - касательная к окружности. Ответ: а) да; б) нет; в) да. IV. Самостоятельная работа К первой задаче из самостоятельной работы записать краткое решение (можно на рисунке); ко второй задаче - полное решение. 1уровень I вариант 1. Прямая КЕ касается окружности с центром в точке О, К— точка касания. Найдите ОЕ, если КЕ = 8 см, а радиус окружности равен 6 см. 2. В треугольнике АВС АВ = 4 см, ВС = 3 см, АС = 5 см. Докажите, что АВ - отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом, равным 3 см. II вариант 1. Прямая МNкасается окружности с центром в точке О, М- точка касания, МNО = 30°, а радиус окружности равен 5 см. Найдите N0.2. В треугольнике МNК МN = 6см, МК = 8 см, NК = 10 см. Докажите, что МК - отрезок касательной, проведенной из точки К к окружности с центром в точке N и радиусом, равным 6 см. II уровень I вариант 1. АВ и ВС - отрезки касательных, проведенных к окружности с центром О и радиусом, равным 10 см. Найдите ВО, если АОС = 60°.2. Докажите, что основание АС равнобедренного треугольника АВС является касательной окружности с центром в точке В и радиусом, равным медиане треугольника, проведенной к его основанию. II вариант 1. МNи NК - отрезки касательных, проведенных к окружности с центром О, MNК = 90°. Найдите радиус окружности, если ОN= 2 см.2. Докажите, что стороны равностороннего треугольника касаются окружностей, проведенных с центрами в его вершинах и радиусами, равными любой из его биссектрис. III уровень I вариант 1. ЕК и ЕF - отрезки касательных, проведенных к окружности с центром О и радиусом, равным 6 см, КОF = 120°, А - точка пересечения КFи ОЕ. Найдите ОА и АЕ.2. Даны угол и отрезок. Постройте окружность радиусом, равным данному отрезку, касающуюся сторон данного угла. II вариант 1. РМ и РN - отрезки касательных, проведенных к окружности с центром О и радиусом, равным 10 см, МОN= 120°, Е - точка пересечения МNи ОР. Найдите ОЕ и РЕ.2. Даны угол и отрезок. Постройте окружность, касающуюся сторон данного угла, с центром, удаленным от вершины угла на расстояние, равное длине данного отрезка. V. Подведение итогов урока Домашнее задание Решить задачи № 641, 643, 645, 648. |