|
|
Треугольники. Урок обобщающего повторения по геометрии в 9м классе на тему "Треугольники"
Урок обобщающего повторения
по геометрии в 9-м классе на тему: "Треугольники"
Тип урока: урок обобщения и систематизации знаний.
Цель: систематизировать и обобщить знания учащихся по теме «Треугольники»; способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения; способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях; содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.
Задачи:
Выявить уровень подготовки учащихся по геометрии по данной теме.
Закрепить знания учащихся о методах решения треугольников, знание теорем о сумме углов треугольника, синусов, косинусов, тангенсов и котангенсов углов, теоремы Пифагора, теорем синусов и косинусов, отрабатывать навыки применения их в ходе решения задач.
Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда.
Научить учащихся находить главное.
Продолжить воспитание у учащихся уважительного отношения друг к другу
План урока:
Организационный момент.
Устная работа: проверка теоретических знаний.
Тестовая работа
Решение теста по теореме Пифагора в парах.
Решение индивидуального теста
Подведение итогов урока.
Домашнее задание
Планируемые результаты:
Предметные:
Уметь решать задачи базового и повышенного уровней сложности по теме «Треугольники. Вычисление углов и длин».
Метапредметные:
Уметь анализировать, сравнивать, обобщать, делать выводы, работать в группе, продолжить развивать пространственное мышление.
Личностные:
Уметь строить отношения в коллективе на основе взаимного уважения и чувства взаимной ответственности, воспитывать самостоятельность
ХОД УРОКА
Технология проведения
|
Деятельность
учеников
|
Деятельность
учителя
|
Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов
|
Планируемые результаты
|
Предметные
|
УУД
|
I.Этап мотивации к учебной деятельности
Цель: организация самооценки учащимися, готовности к предстоящей деятельности на уроке, формирование положительной мотивации к освоению содержания урока.
|
Включаются в деловой ритм урока.
Слушают учителя
Формулируют тему и ставят цель урока
|
Приветствует учащихся, контролирует готовность к уроку,
Говорит:
Треугольник – геометрическая фигура, знакомая с уроков геометрии начиная с 7 класса. За 3 года вы познакомились со многими теоремами, свойствами, связанными с этой фигурой. В 10-11 классах тоже применяются решения треугольников, поэтому вы должны научиться решать любую задачу связанную с этой фигурой.
Как вы думаете какая тема нашего урока?
Какую цель мы будем реализовывать?
Давайте попробуем это сделать?
|
|
|
Регулятивные УУД: способность к саморегуляции.
Личностные УУД:
формирование способности к восприятию материала.
|
II. Этап актуализации и пробного учебного действия
Цель: организация восприятия знания учащимися, актуализация опорных знаний и способов действий.
|
Отвечают на вопросы учителя. Формулируют определение треугольника, перечисляют элементы треугольников, их виды, свойства.
Формулируют теорему Пифагора
Формулируют определения синуса, косинуса, тангенса
Перечисляют признаки равенства треугольников
Работают с текстом
.
|
Организует беседу по теме «Треугольники».
Подключает интерактивную доску, проектор. Просит найти ошибки в тексте
|
Вопросы:
1. Какую фигуру называют треугольником?
2. Перечислите элементы треугольника.
3. Назовите виды треугольников по углам.
4. Назовите виды треугольников по сторонам.
5. Какой треугольник называется равносторонним?
6. Перечислите свойства равнобедренного треугольника.
7. Сформулируйте теорему Пифагора.
8. Сформулируйте определение синуса, косинуса, тангенса угла прямоугольного треугольника?
9. Перечислите признаки равенства треугольников.
10. В треугольнике KLN, KL=8,4 cм, LN=13,2 см, KN=7,5 см. Какой угол треугольника наибольший, какой наименьший?
11. Стороны треугольника 10см, 12см, 7см. Может ли угол, противолежащий стороне 7см, быть тупым? Почему?
Найдите ошибки в тексте:
1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой
3. Прямая, параллельная стороне треугольника, является его средней линией.
4. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны
5. Площадь любого треугольника можно вычислить по формулам:
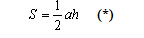
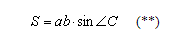
|
Треугольник, его элементы, свойства треугольника, виды треугольников. Теорема Пифагора. Синус, косинус, тангенс угла
|
Познавательные
УУД:
- структурирование знаний;
- анализ объектов с выделением их существенных и несущественных признаков;
-осознанное построение речевого высказывания в устной форме.
Коммуникативные УУД- умение вести диалог, учитывать разные мнения в сотрудничестве.
|
III Этап выявления места и причины затруднения
Цель: выявить возникшее затруднение и пробелы в знаниях
|
Выполняют тестовые задания индивидуально
Работают в парах выполняют тестовые задания
Взаимопроверка работы
|
Предлагает самостоятельно решить тест на применение тех теоретических знаний, которые повторили в начале урока.
Предлагает поработать в парах и выполнить вторую часть тестовой работы
Организует взаимопроверку тестовой работы. С помощью проектора проецирует на интерактивную доску ответы к тестовой работе
|
*
**
|
Треугольник, его элементы, свойства треугольника, виды треугольников. Теорема Пифагора. Синус, косинус, тангенс угла
|
Познавательные УУД:
формулировать информационный запрос, самостоятельно выделять познавательную цель.
Регулятивные УУД:
-контроль;
-саморегуляция
Коммуникативные УУД:
умение вести диалог, высказывать и обосновывать свое мнение, слушать собеседника
|
IV Этап построения проекта выхода из затруднительной ситуации
Цель: постановка целей учебной деятельности, обобщение знаний по теме «Треугольники», решение более сложных задач
|
Отвечают на вопросы учителя.
Формулируют конкретные цели своих учебных действий, решают более сложные задачи
|
Организует обсуждение в группах
|
|
|
Регулятивные УУД:
-целеполагание;
-планирование.
|
V Этап реализации построенного проекта
Цель: связать изученные в рамках темы понятия в единую систему посредством совместного решения задачи, требующей большого количества теоретических фактов
|
Фиксируют знание в устной и письменной форме.
|
Организует отчет групп.
На интерактивной доске представитель группы восстанавливает пропущенное решение.
|
1 группа. Задача1
 2 группа Задача 2 2 группа Задача 2
3 группа. Задача 3.
|
|
Познавательные УУД:
- структурирование знаний;
- выбор наиболее рациональных способов решения задач в зависимости от условий.
Личностные УУД:
критичность мышления
|
VI Рефлексия деятельности на уроке
Цель: инициировать рефлексию учащихся по поводу эмоционального состояния, мотивации, их собственной деятельности и взаимодействия с учителем и одноклассниками в классе
|
Отвечают на вопросы.
|
Закрепляет на доске вырезанные из бумаги модели четырехугольников разных цветов. На обороте записаны вопросы.
Приглашает ученика (по его желанию) тот выбирает модель бабочки и отвечает на вопрос, размещенный на обороте, затем он сам выбирает, кому передает ход.
|
Что на уроке было самым простым?
Что на уроке было самым сложным?
Что было на уроке самым интересным?
|
| Регулятивные УУД: -структурируют знания, осознают качество и уровень усвоения, способность к самооценке; -саморегуляция.
|
VII Информация о домашнем задании
Цель: обеспечение понимания учащимися цели, содержания и способов выполнения домашнего задания.
|
Получают карточки с домашним заданием
|
Формулирует домашнее задание
|
|
|
|
* тестовая работа (индивидуальная):
№
|
1 вариант
|
2 вариант
|
1
|
Какие из следующих утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.
4) В треугольнике ABC, для которого 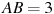 , , 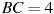 , , 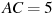 , угол С , угол С  наименьший. наименьший.
|
Какое из следующих утверждений верно?
1) В треугольнике против меньшего угла лежит большая сторона.
2) Если один угол треугольника больше 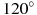 , то два других его угла меньше , то два других его угла меньше 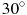 . .
3) Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
4) Сумма острых углов прямоугольного треугольника не превосходит 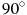 . .
|
2
|
Какие из следующих утверждений верны?
1) В треугольнике 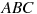 , для которого , для которого 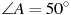 , , 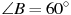 , , 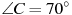 , сторона , сторона 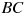 — наименьшая. — наименьшая.
2) Любые два равнобедренных треугольника подобны.
3) Внешний угол треугольника больше каждого внутреннего угла.
4) Треугольник со сторонами 1, 2, 3 не существует.
|
Какие из следующих утверждений верны?
1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
2) В треугольнике 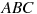 , для которого , для которого 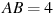 , , 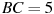 , , 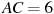 , угол , угол 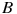 — наибольший. — наибольший.
3) Любые два прямоугольных треугольника подобны.
4) Треугольник ABC, у которого 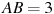 , , 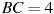 , , 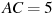 , является тупоугольным. , является тупоугольным.
|
3
|
Какое из следующих утверждений верно?
1) Около всякого треугольника можно описать не более одной окружности.
2) В любой треугольник можно вписать не не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
|
Какие из следующих утверждений верны?
1) Около всякого треугольника можно описать не менее одной окружности.
2) В любой треугольник можно вписать не более одной окружности.
3) Центром окружности, вписанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, описанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
|
** Решение теста на применение теоремы Пифагора (в парах)
4. Укажите, какой из рисунков содержит треугольники, к которым применима теорема Пифагора.

5. Сторона квадрата равна 3 см, тогда его диагональ равна:
а) 9 см; б) 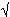 6 см; в) 6 см; в) 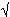 3 см; г) 3 3 см; г) 3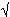 2 см. 2 см.
6. В равнобедренном треугольнике боковая сторона равна 10 см, а основание – 16 см, тогда высота опущенная на основание, равна:
а) 241 см; б) 6см; в) 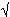 26 см; г) 26 см; г) 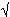 6 см. 6 см.
7. Из одной точки на прямую опущены перпендикуляр и наклонная. Если перпендикуляр равен 9 см, а наклонная – 15 см, то длина проекции наклонной равна:
а) 12 см; б) 3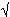 34 см; в) 2 34 см; в) 2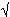 6 см; г) 6 см; г) 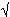 6 см. 6 см.
8. Из точки D к окружности с центром в точке о проведена касательная DF. Если OD=17 см, а FD=15 см, то радиус окружности равен:
а) 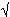 2 см; б) 8 см; в) 32 см; г) 4 2 см; б) 8 см; в) 32 см; г) 4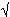 2 см. 2 см.
9. Дан прямоугольный треугольник ABC. Гипотенуза AC=10 см, sinC=0,3. найдите катет AB.
10. В прямоугольном треугольнике ABC:AC=17 см, BC=8 см, AB=15 см. найдите cosC. |
|
|
 Скачать 122 Kb.
Скачать 122 Kb.