Геометрия.Изображение. Задача 1 Анализ
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Задача №1 Анализ: Так ромб с углом 600, то треугольник ADC равносторонний, и высота ромба будет являться и медианой, т.е. точка К середина стороны ромба. Если на высоте ромба строить равносторонний треугольник, то возможны два случая. Случай 1 Треугольник расположен внутри ромба. 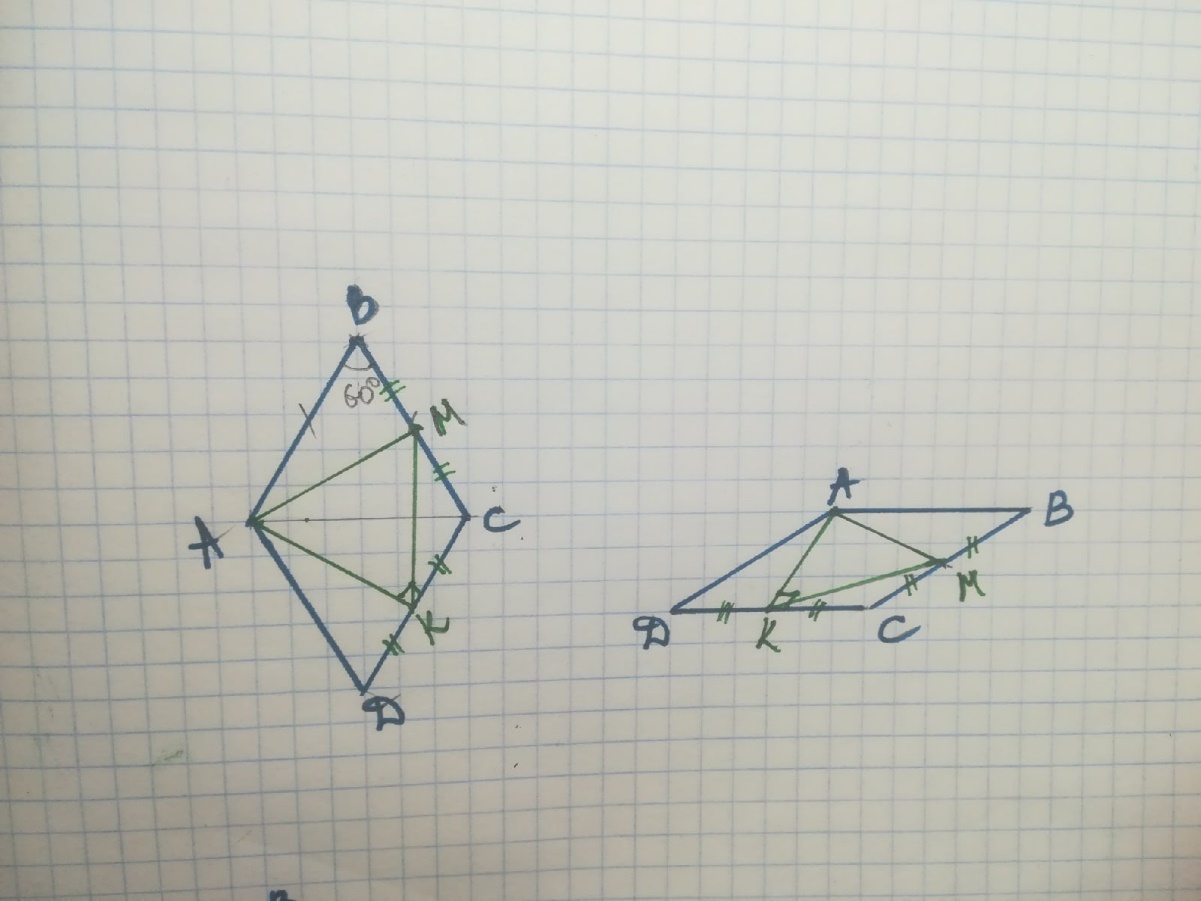 Анализ: Треугольник расположен внутри ромба. Точки К и А две вершины равностороннего треугольника Угол КАС равен 30о. Диагональ ромба АС будет биссектрисой и медианой для будущего треугольника. Следовательно, третья вершина треугольника принадлежит стороне ВС, и так же лежит на его середине. Таким образом, чтобы построить образ равностороннего треугольника на высоте ромба, достаточно соединить вершину ромба, из которой опущена высота, с серединами противоположных сторон. Построение: 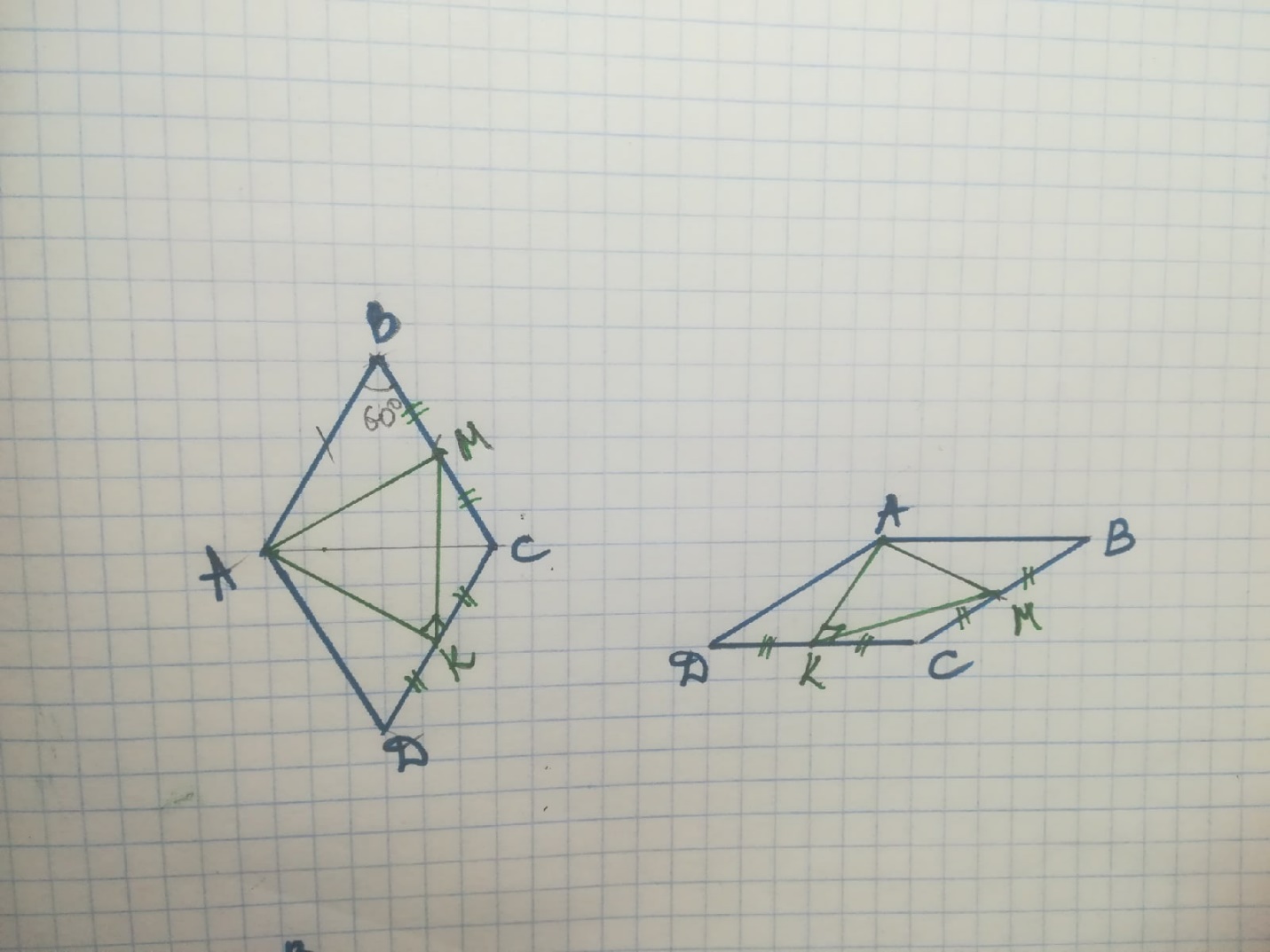 Построить К – середина DC, АК – высота ромба Построить M – середина BC Соединить К и М. Треугольник АКМ - искомый Случай 2 Треугольник расположен вне ромба. 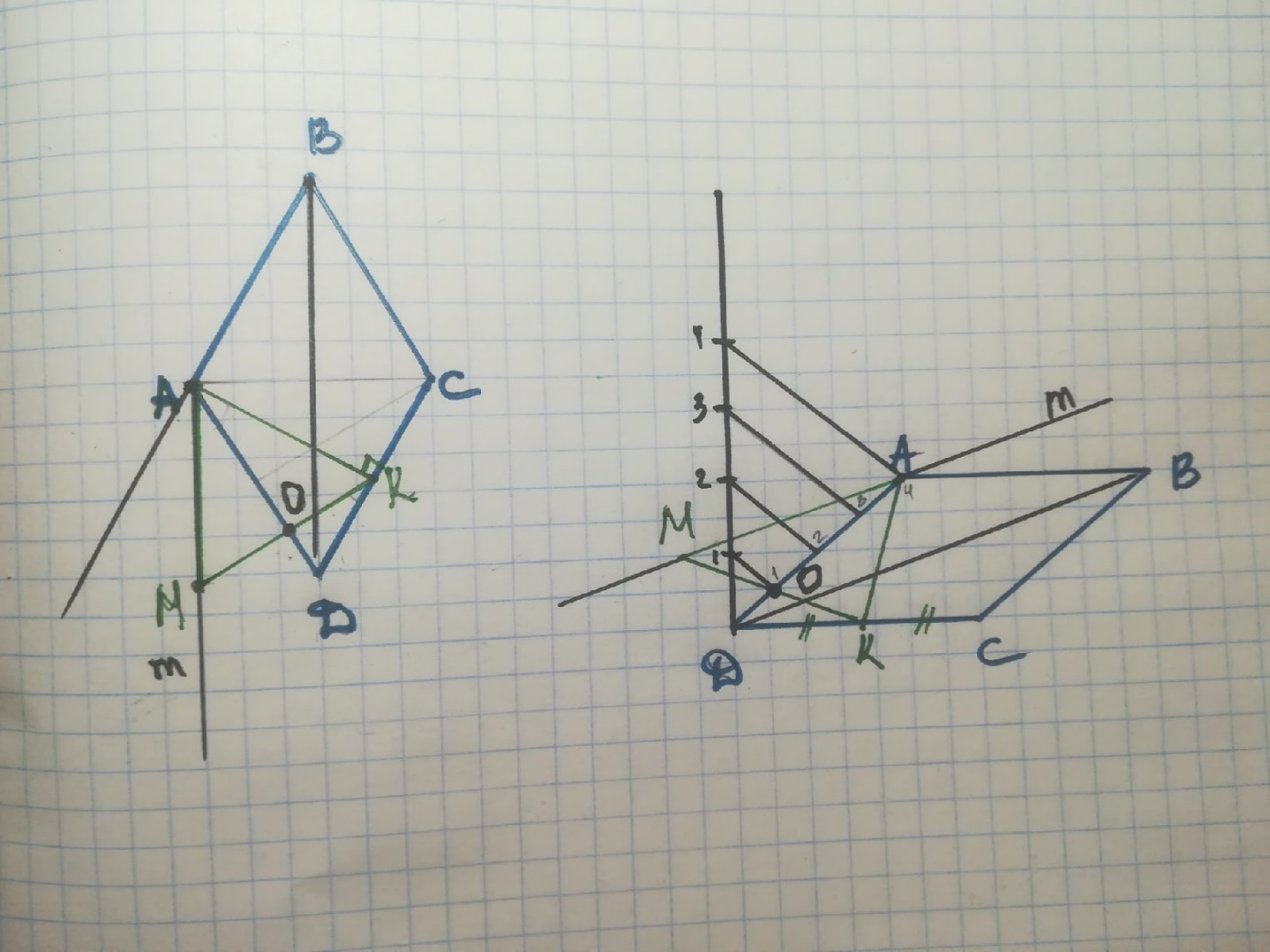 Анализ: Точки К и А две вершины равностороннего треугольника. Угол КАО и угол DAM =30o Таким образом прямые m и BD параллельны МК пересекает AD в точке О. Из треугольника КОD (прямоугольный с углом ОКD в 30o) ОК равна половине KD. Так как СD=DA, то OD=1/4AD. Значит, чтобы построить точку О достаточно на отрезке AD считая от вершины отметить четвертую часть (по теореме Фалеса). Соединить К (середину DC) c точкой О. КО пересечет прямую m в точке М –третья вершина искомоготреугольника. Построение: 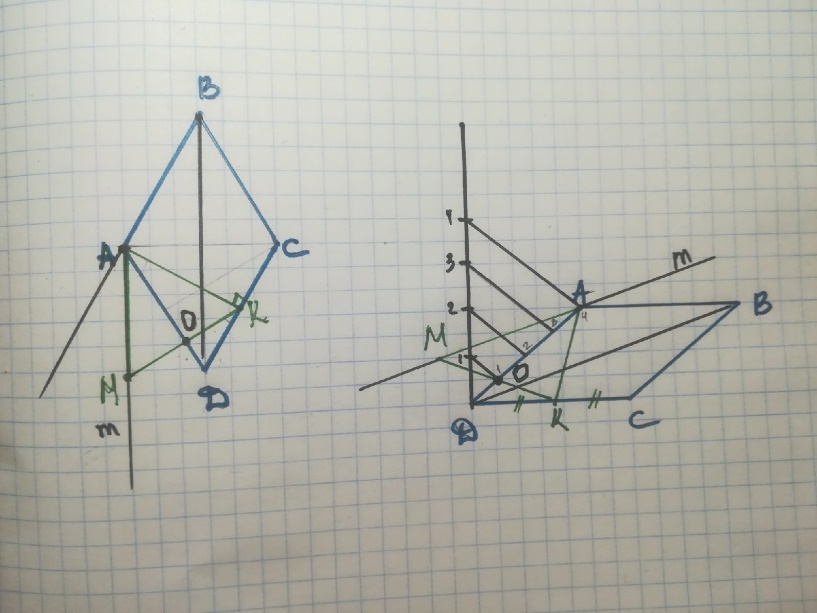 Построить К – середина DC, АК – высота ромба Через точку А провести прямую m параллельно DB По теореме Фалеса разделить AD на 4 отрезка: DO=1/4DA Провести прямую КО: КО пересекает прямую m в точке М, АМК искомый равносторонний треугольник Задача №2 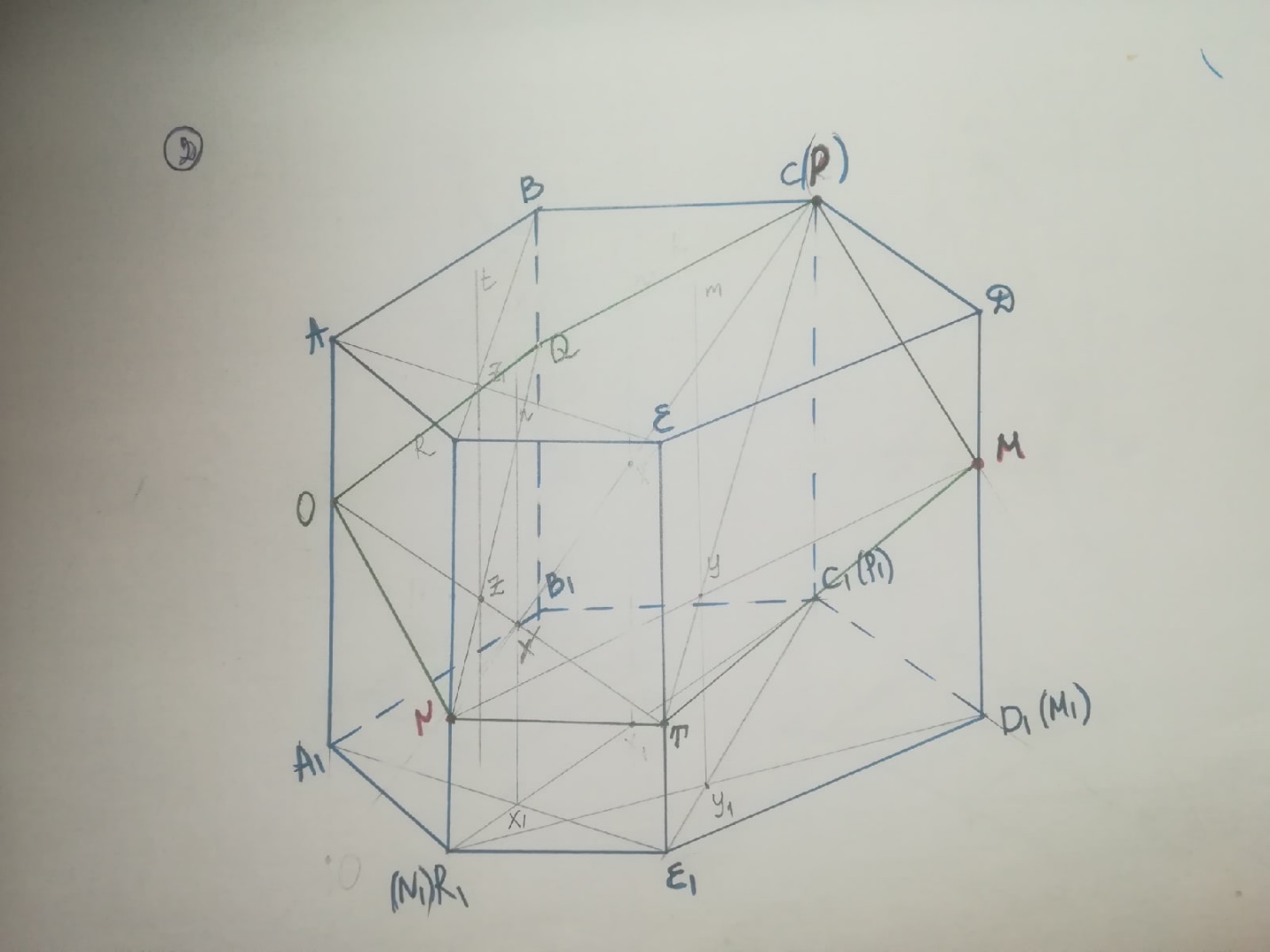 Анализ: Если заданы точки M, N, P, то заданы и их вторичные проекции M1,N1,P1. M1 совпадает с точкой D1,N1 совпадает с точкой R1, P1 совпадает с точкой C1 В грани D1CD лежит две точки (P и M), принадлежащие сечению, мы можем провести через них прямую PM Найдем дополнительные точки в грани EDD1 методом внутреннего проектирования. Для этого в плоскости нижнего основания призмы возьмем четыре точки, три из которых принадлежат сечению, а одна является вершиной. Пусть это будут точки С1, D1, E1 и R1. Проведем диагонали полученного четырехугольника С1E1 и D1R1, которые пересекаются в точке Y1. Найдем для точки Y1 оригинал, для этого проведем через Y1 прямую m параллельную боковому ребру. Так как Y1 лежит на проекции M1N1, то оригинал точки Y1 будет лежать на оригинале MN. MN пересекает m в точке Y. Теперь проведем PY, PY пересекает ребро EE1 в точке T – она является искомой точкой оригиналом для точки E1, и в то же время принадлежит сечению. В грани EDD1 имеется две точки сечения TM. Соединим их. В грани ERE1 имеется так же имеется две точки сечения T и N. Соединим их. Найдем дополнительные точки в грани ARR1 методом внутреннего проектирования. Для этого в плоскости нижнего основания призмы возьмем четыре точки, три из которых принадлежат сечению, а одна является вершиной. Пусть это будут точки С1, A1, E1 и R1. Проведем диагонали полученного четырехугольника Найдем для точки X1 оригинал, для этого проведем через X1 прямую n параллельную боковому ребру. Так как X1 лежит на проекции C1N1, то оригинал точки X1 будет лежать на оригинале CN. CN пересекает n в точке X. Теперь проведем TX, TX пересекает ребро AA1 в точке O – она является искомой точкой оригиналом для точки A1, и в то же время принадлежит сечению. Таким образом в грани ARR1 имеется две точки сечения NO. Соединим их. Найдем теперь дополнительные точки в грани ABB1 методом внутреннего проектирования. Для этого в плоскости верхнего основания призмы возьмем четыре точки, три из которых принадлежат сечению, а одна является вершиной. Пусть это будут точки B, A, E и R. Проведем диагонали полученного четырехугольника AE и BR, которые пересекаются в точке Z1. Найдем для точки Z1 оригинал, для этого проведем через Z1 прямую t параллельную боковому ребру. Так как Z1 лежит на проекции AE, то оригинал точки Z1 будет лежать на оригинале OT. OT пересекает t в точке Z. Теперь проведем NZ, NZ пересекает ребро BB1 в точке Q – она является искомой точкой оригиналом для точки B, и в то же время принадлежит сечению. Таким образом в грани ABB1 имеется две точки сечения QO. Соединим их. В грани СBB1 так же имеется две точки сечения QС. Соединим их. В результате получили искомое сечение CMTNOQ Построение: Провели PM в грани D1CD. Проведем диагонали четырехугольника С1D1E1R1: С1E1 и D1R1 пересекаются в точке Y1 m параллельна боковому ребру MN пересекает m в точке Y PY пересекает EE1 в точке T В грани EDD1 соединим TM. Проведем диагонали четырехугольника С1A1R1E1: A1E1 и C1R1 пересекаются в точке X1. n параллельна боковому ребру CN пересекает n в точке X. TX пересекает ребро AA1 в точке O в грани ARR1 соединим NO. Проведем диагонали четырехугольника BARE: AE и BR пересекаются в точке Z1. t параллельна боковому ребру OT пересекает t в точке Z NZ пересекает BB1 в точке Q в грани ABB1 соединим QO. грани СBB1 соединим QС. CMTNOQ - искомое сечение Задача №3 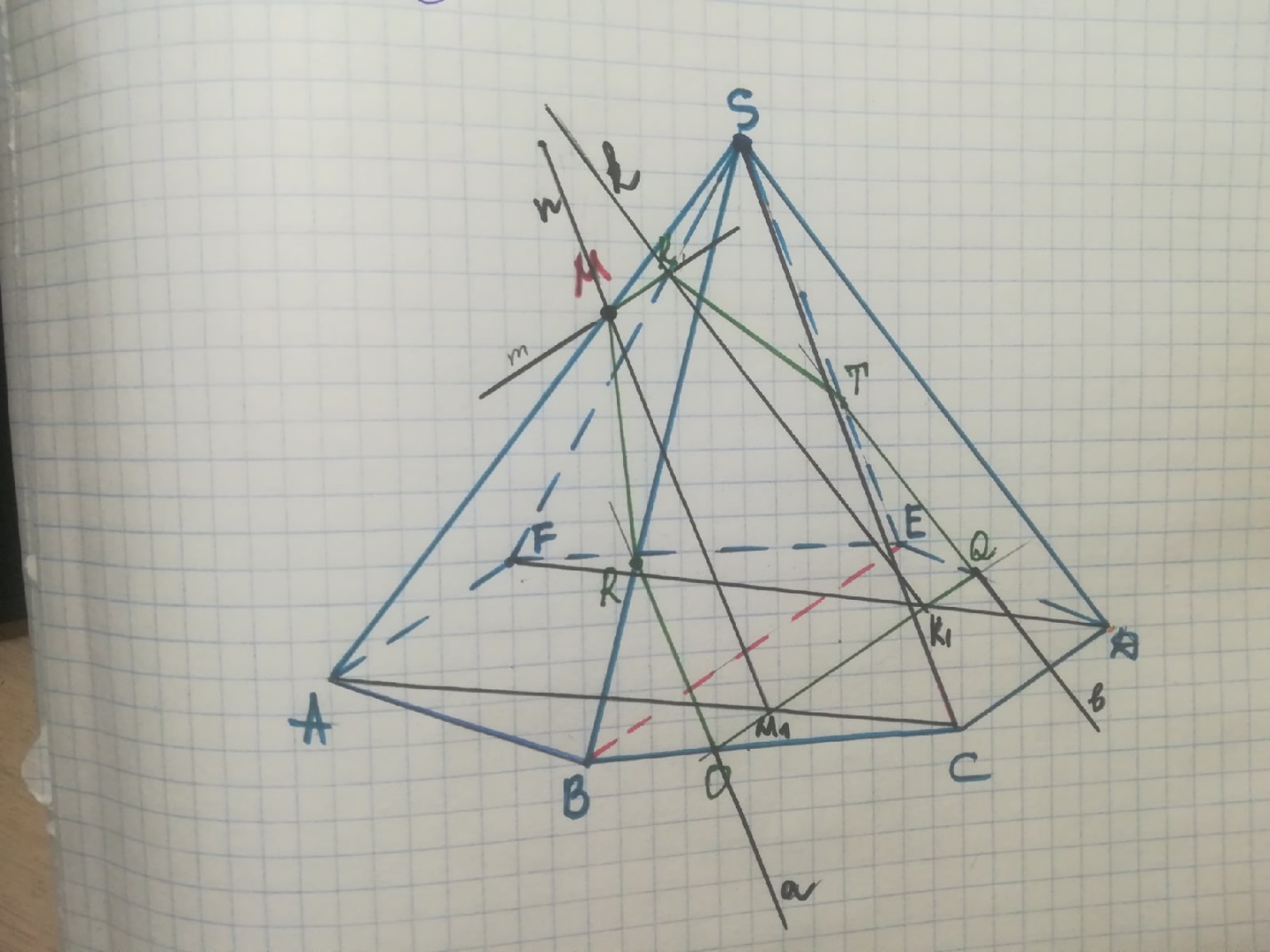 Анализ Определим плоскость параллельную одновременно двум прямым SC и BE. Пусть наша плоскость содержит одну из данных прямых, например, прямую SC, тогда нужно определить прямую параллельную BE, и при этом проходящую через прямую SC. Так как пирамида правильная, значит в ее основании лежит правильный 6-уголник. По свойству правильного 6-угольника большая его диагональ параллельна противоположной стороне. Таким образом DC параллельна BE, следовательно, плоскость параллельная (SC) и (BE) это плоскость SCD. Значит нам нужно построить сечение параллельное плоскости SCD. В грани ASF имеется точка M – точка сечения, через нее построим прямую m параллельно плоскости SCD. AF параллельна CD (По свойству правильного 6-угольника), значит AF параллельна плоскости SCD. Поэтому в плоскости ASF через точку М построим прямую m параллельную AF. Прямая m пересекает боковое ребро в точке К – это точка сечения. Точки М и К лежат в одной грани, поэтому соединим их, получим отрезок МК – принадлежит сечению. Найдем дополнительные точки. Так как искомое сечение параллельно плоскости SCD, то построим плоскость содержащую прямую SC и прямую AS (на которой лежит точка М). В плоскости ASC через точку М построим прямую n параллельно прямой SC. Прямая n пересекает прямую АС в точке M1. Найдем еще дополнительные точки. Построим плоскость содержащую прямую SD и прямую FS (на которой лежит точка N). В плоскости SFD через точку N построим прямую k параллельно прямой SD. Прямая k пересекает прямую FD в точке K1. Точки M1 и K1 лежат в сечении, так как параллельны плоскости SDC и лежат в одной плоскости с точками сечения M и K. Продлим прямую M1K1 до пересечения со сторонами основания. M1K1 пересекает BC в точке О – точка сечения M1K1 пересекает BC в точке Q – точка сечения/ OQ – отрезок сечения Найдем дополнительные точки для О и Q. В грани SBC через точку О проведем прямую a параллельно SC Прямая а пересекает ребро SB в точке R. RO – отрезок сечения В грани SDE через точку Q проведем прямую b параллельно SD Прямая b пересекает ребро SE в точке T. TQ – отрезок сечения. Таким образом в грани ABS есть две точки сечения R и M. Соединим их. В грани EFS также есть две точки сечения T и K. Соединим их. MROQTK искомое сечение. Построение: Проведем m параллельно AF: Прямая m пересекает SF в точке К Провели KM в грани ASF. Построим плоскость ASC Через точку М построим прямую n параллельно прямой SC: прямая n пересекает прямую АС в точке M1 Построим плоскость SFD Через точку K построим прямую k параллельно прямой SD: прямая k пересекает прямую DF в точке K1 Продлим прямую M1K1 M1K1 пересекает BC в точке О – точка сечения M1K1 пересекает BC в точке Q – точка сечения/ OQ – отрезок сечения проведем прямую a параллельно SC через точку О в грани SBC Прямая а пересекает SB в точке R. RO – отрезок сечения В грани SDE через точку Q проведем прямую b параллельно SD Прямая b пересекает ребро SE в точке T. TQ – отрезок сечения. Соединим R и M. Соединим T и K. MROQTK - искомое сечение. |
