Карта интегрированного урока математики 10 класс "Мгновенная скорость". Карта интегрированного урока математики 10 класс "Мгновенна. Урок по теме Мгновенная скорость, угловой коэффициент и предельные издержки. Цель урока
 Скачать 126.5 Kb.
|
|
Интегрированный урок по теме: «Мгновенная скорость, угловой коэффициент и предельные издержки». Цель урока: установление причинно-следственных связей между явлениями и понятиями, общих закономерностей при решении задач, из разных областей знаний. Обучающая: усвоение понятия производной через геометрический, физический и экономический смысл в ходе решения задач из разных наук – физики, экономики и математики. Развивающая: формирование навыков концептуальных основ мышления, установление причинно-следственных связей между явлениями и понятиями. Воспитательная: развитие у учащихся целостного восприятия математической науки как основного аппарата для описания физических и экономических явлений. Это интегрированный урок обобщения и систематизации знаний. Структура урока.
VI. Домашнее задание. Мгновенная скорость, угловой коэффициент и предельные издержки. I этап. Мотивация учебной деятельности. Казалось бы, ничего нет общего между понятиями мгновенная скорость, угловой коэффициент и предельные издержки. Одно из них заимствовано из механики, второе из математики, а третье из экономики. Что же их объединяет? Чтобы ответить на этот вопрос, мы рассмотрим три задачи, но вначале вспомним такое понятие, как функция. Функция это зависимость между двумя переменными, где каждому значению независимой переменной соответствует единственное значение зависимой переменной. В экономике рассматриваются производственные функции. Возможности любого производства определяются характером зависимости между объёмом выпускаемой продукции и соответствующими ему затратами сырья, энергии, труда, капиталовложений и т. д. Всевозможные затраты это факторы производства или ресурсы. Они имеют различные единицы измерения (тонны, метры, киловатт-часы и др.). Единицей измерения ресурсов может служить рубль или др. Функция, выражающая зависимость между стоимостью выпускаемой продукции и стоимостью суммарных затрат на её производство, называется однофакторной производственной функцией. Независимая переменная затраты; зависимая переменная уровень выпуска. Пример 1) y = a1x + a0 (a1 > 0; a0 > 0;  ), где y затраты на производство продукции; a0 условно-постоянные затраты; a1x условно-переменные затраты.Пример 2)  затраты на единицу выпускаемой продукции от объёма производства x.II этап. Повторение ранее изученного материала Рассмотрим три задачи на нахождение предела отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
(Ответ ученика). Закон движения материальной точки описывается функцией f, выражающей зависимость пути S от времени t:       S  0 путь, пройденный точкой к моменту времени t; путь, пройденный точкой к моменту времени  .За время  точка прошла путь  .За время средняя скорость равна  .Скорость движения в каждый конкретный момент времени отличается от средней скорости. Но чем короче отрезок , тем меньше различие между скоростями.  И  так: 2. Вычислить угловой коэффициент касательной к графику функции f(t) в точке с абсцисой  .Определение секущей и касательной. Секущая это прямая, проходящая через точки M1(x1; f (x1)) и M2(x2; f (x2 )). Касательной к графику функции 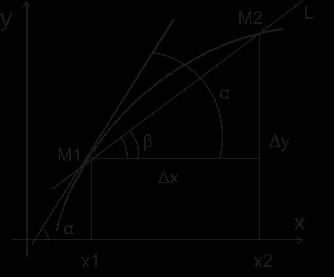 в точке M1 называют предельное положение секущей M1M2при условии, что точка M2вдоль кривой стремится к M1. (Можно дать ещё 2 определения касательной.)  Угловой коэффициент касательной к графику функции f(x) в точке с абсциссой  равен: 3. Вычислить предельные издержки производства при объеме производства х если функция затрат задана формулой f(x). Пусть x объём производства некоторой продукции. K суммарные затраты (издержки производства). K = f(x) функция затрат, описывает зависимость издержек производства K от объёма x выпускаемой продукции. Если объём производства увеличится на  единиц, то затраты возрастут на  единиц. среднее приращение издержек. предельные издержки. (Это дополнительные затраты на производство продукции при увеличении объёма производства на малую единицу, если исходный объём производства x единиц.) То есть  .Итак, мы видим, что решение каждой из задач приводит к необходимости нахождения предела отношения приращения функции к вызвавшему его приращению аргумента, когда последнее стремится к нулю. III этап.Анализ основных фактов. Схема решения всех задач следующая.
 ;
По этой же схеме можно решать задачи на отыскание плотности тела в данной точке, скорости протекания химических реакции в данный момент времени, теплоёмкости тела при данной температуре, скорости изменения спроса на товар при данной цене и др. В конечном итоге всё это задачи на нахождение производной функции  .IV этап. Выполнение практических заданий. Рассмотрим ряд примеров, при решении которых пригодятся имеющиеся у вас знания и выводы из рассмотренных задач.
S = 3 + t + t2 движется ускоренно. Найти его мгновенную скорость в момент времени t1= 2; t2= 4. Какова начальная скорость и средняя скорость на отрезке времени от t=1 до t=4? (Ответ: V(1) = 3; V(4) = 9; V(0) = 1; V(2) = 5; Vср[1; 4] = 6.)
(Ответ:    )
y = f(x) в точке (x0; f(x0)) (Ответ: y = f(x0) + f’(x0)(x-x0).)
(Решение:    K’(8) < K’(3) Ошибка! Объект не может быть создан из кодов полей редактирования.то есть если объём увеличивается, то предельные издержки дополнительные затраты на следующую за x малую единицу объёма уменьшаются.)
 , где p цена.Определить скорость изменения спроса, когда цена на товар составляет 1; 4 денежных единицы. (Решение:  ;d’(1) = -25, d’(4) = -4. С увеличением цены спрос на товар убывает.)
x = 20 + 8r - r2, а затраты ресурса составляют r = 2; 5 условных единиц. (Решение: x’=8-2r x’(2)=8-4=4 x’(5)=8-10=-2 С увеличением затрат данного ресурса выпуск уменьшается, производство данного товара становится экономически невыгодным.) Решение данных задач нам позволяет сделать вывод о том, что с увеличением объема производства предельные издержки (дополнительные затраты) убывают, если производная функции затрат принимает положительное значение, а сама функция затрат является убывающей функцией. Если производная поизводственной функции зависимости спроса на товар от цены принимает отрицательное значение, то это означает, что с увеличением цены спрос на товар убывает. V этап. Подведём итоги. Из определения производной и рассмотренных задач вытекает:
Как производные производственных функций, вычисляются и многие другие экономические показатели, такие как предельный спрос, предельная выручка, предельная производительность ресурса. С этими величинами, их ролью в экономическом анализе мы встретимся на следующем уроке.
 . Сравните и объясните результаты. |
;
.
функция затрат. Определить предельные издержки при объёме выпуска x1 = 3; x2 = 8.