Урока "Цярпенне і праца дапамогуць табе дабіцца жаданых поспеха"
 Скачать 0.52 Mb.
|
|
Рашэнне сістэм лінейных ураўненняў з дзвюма зменнымі Дэвіз урока: "Цярпенне і праца дапамогуць табе дабіцца жаданых поспехаў". Л.М.Талстой Тып урока: праверка ведаў і ўменняў. Мэты урока: 1) Адукацыйныя: праверка вучняў самастойна прымяняць веды, уменні і навыкі пры рашэнні сістэм лінейных ураўненняў з дзвюма зменнымі, паўтарэнне і замацаванне пройдзенага матэрыяла; 2)Развіваючая: садзейнічаць развіццю лагічнага мышлення, умення выконваць параўнальны аналіз аналітычнага і графічнага метадаў рашэння сістэм лінейных ураўненняў; 3) Выхаваўчая: выхаванне пазнавальнай актыўнасці, пачуцця адказнасці, упэўненнасці ў сабе, самастойнасці. Пабуджаць вучняў да самакантролю, узаемакантролю, самааналізу сваёй дзейнасці. Абсталяванне: дошка, крэйда, магнітная дошка, карткі для вусных заданняў, тэставыя заданні, ацэначныя лісты, праверачныя лісты-адказы тэстаў, карткі з заданнямі на дом. Формы работы: франтальная, калектыўная, індывідуальная. Метады навучання: метад праверкі і ацэнкі ведаў (вуснае апытанне, вуснае лічэнне, тэсціраванне, самаправерка). Віды работы: вуснае лічэнне, вуснае апытанне, праца ў дошкі, самастойная работа (выкананне тэставых заданняў). План урока. І. Арганізацыйны момант. ІІ. Актуалізацыя ведаў. 1) Праверка дамашняга задання. 2) Кантрольныя пытанні. 3) Вуснае лічэнне. 4) Вуснае рашэнне. ІІІ. Фізкультхвілінка. ІV. Рашэнне тэставых заданняў (самастойна). V. Работа ў дошкі. VІ. Дамашняе заданне. VІІ. Рэфлексія. Падвядзенне вынікаў урока. Работа вучняў складаецца з 6 этапаў. Вынікі сваёй дзейнасці запісваюцца ў ацэначных лістах. Самаацэнка за ўрок залежыць ад сумы (п) набраных балаў на ўсіх этапах. Ацэначны ліст вучня
Крытэрыі адзнак за заданні: Крытэрыі адзнак за ўрок: Няма памылак - "8-10 "балаў, "8-10 " - 32-36 балаў 1-2 памылкі - "6-7 "балаў, "6-7 " - 24-31 бал 3-4 памылкі - " 3 -5"балаў, "3 -5" - 12-23 балы больш 4 памылак - "1-2"балы "1-2" - менш 12 балаў. Ход урока. І. Арганізацыйны момант. (Аб’яўленне тэмы урока, мэты, дэвіза, плана урока) На сталах вучняў ляжаць ацэначныя лісты. Яны запаўняюцца вучнямі пасля кожнага этапа ўрока. ІІ. Актуалізацыя ведаў. 1) Праверка дамашняга задання. № 2.45(6) Праверыць правільнасць рашэння з рашэннем на дошцы (зараней падрыхтавана на дошцы) Рашэнне. 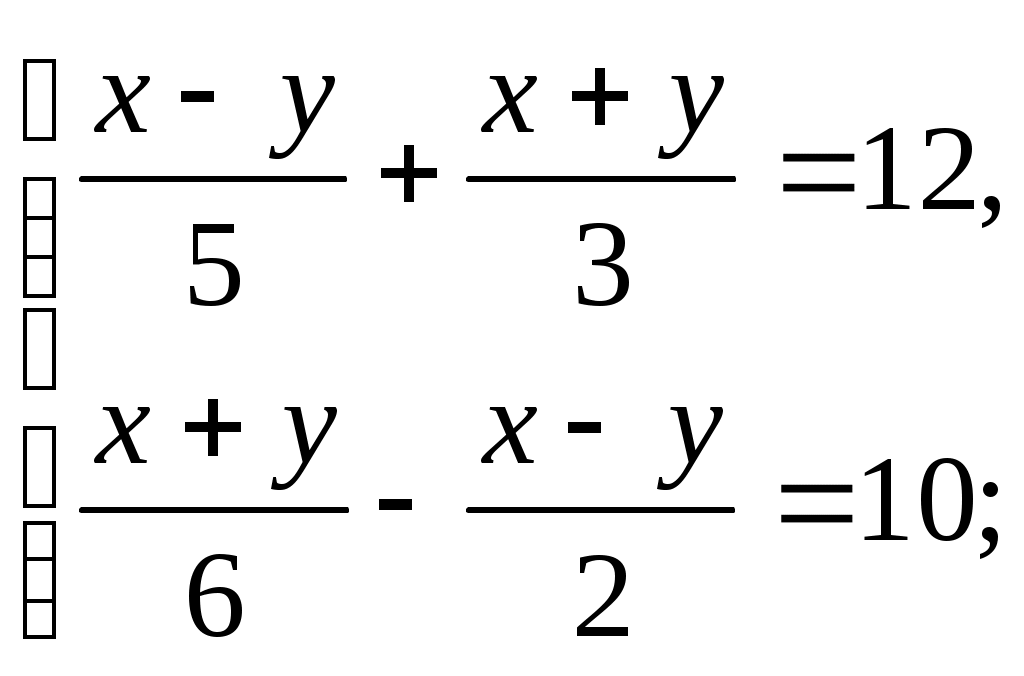 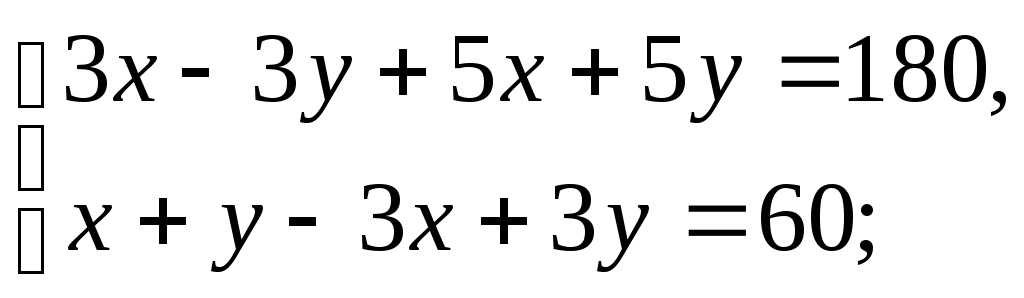     Рэшым другое ўраўненне сістэмы -х+180-8х=30, -9х=-150, 3х=50, х=  Маем 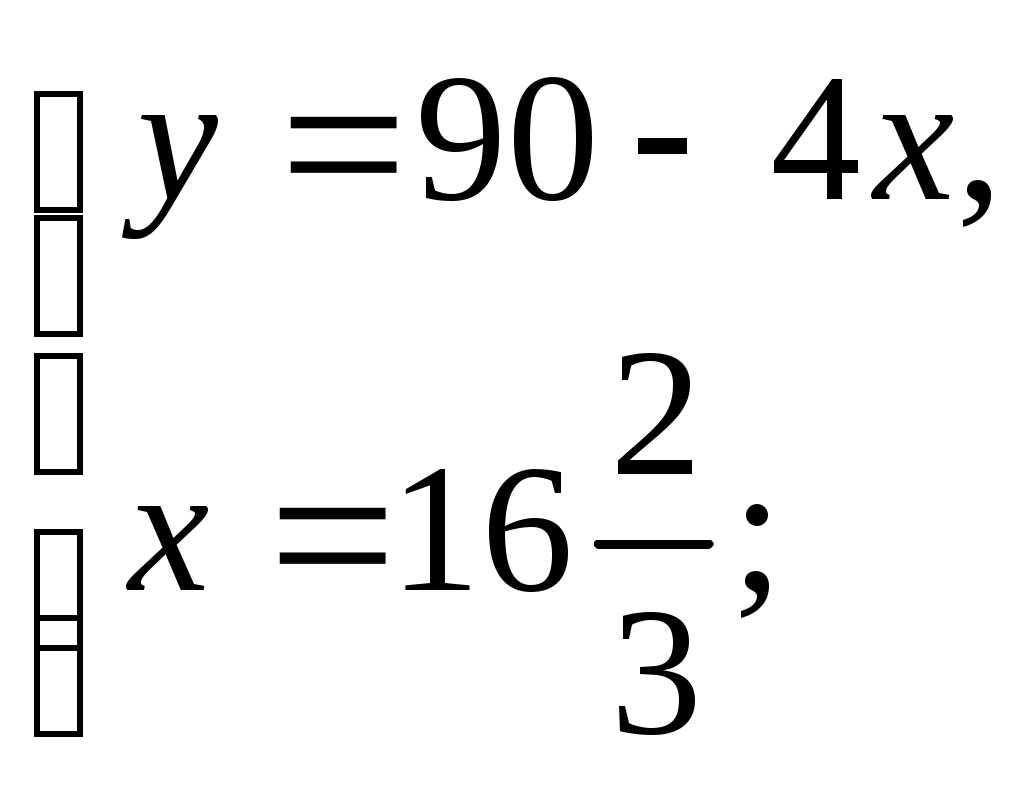  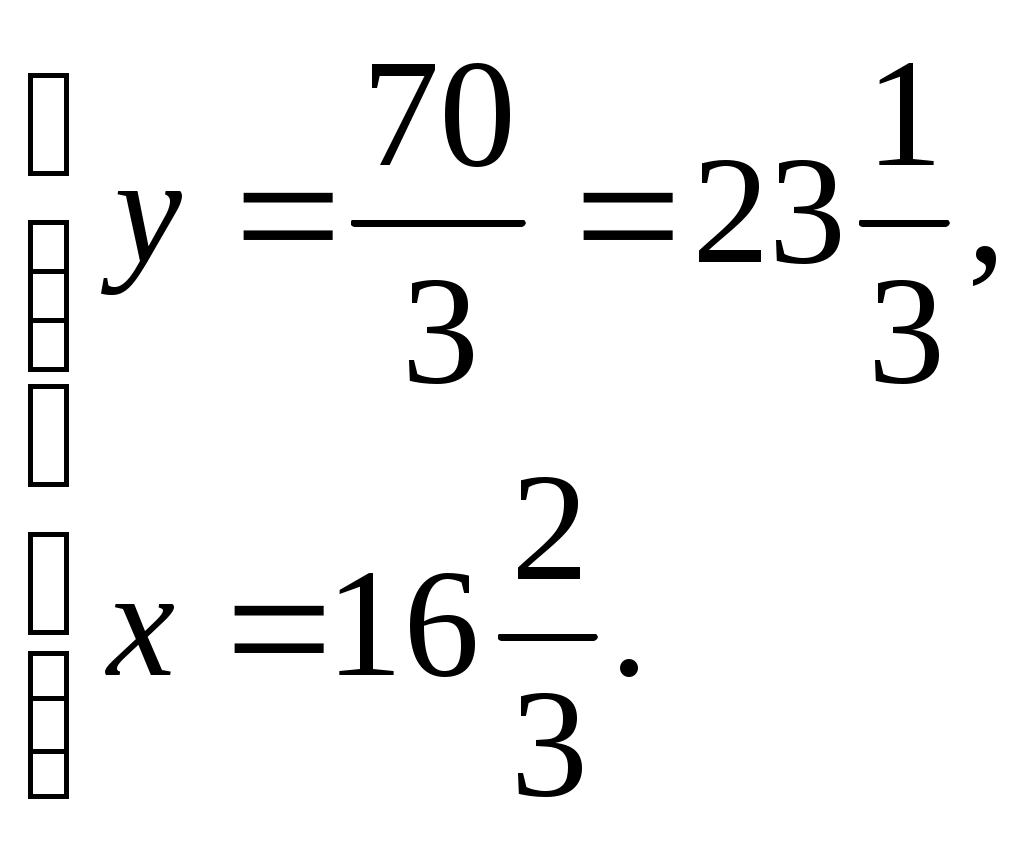 Адказ:  .№ 2.62(3,5) (вусна) Адказы: 3) мае, два пункты; 5) мае, адзін пункт. № 2.64(2) (вусна) Адказ: х2 + у2 = 53. 2) Кантрольныя пытанні. - Як запісваюць сістэму лінейных ураўненняў з дзвюма зменнымі? 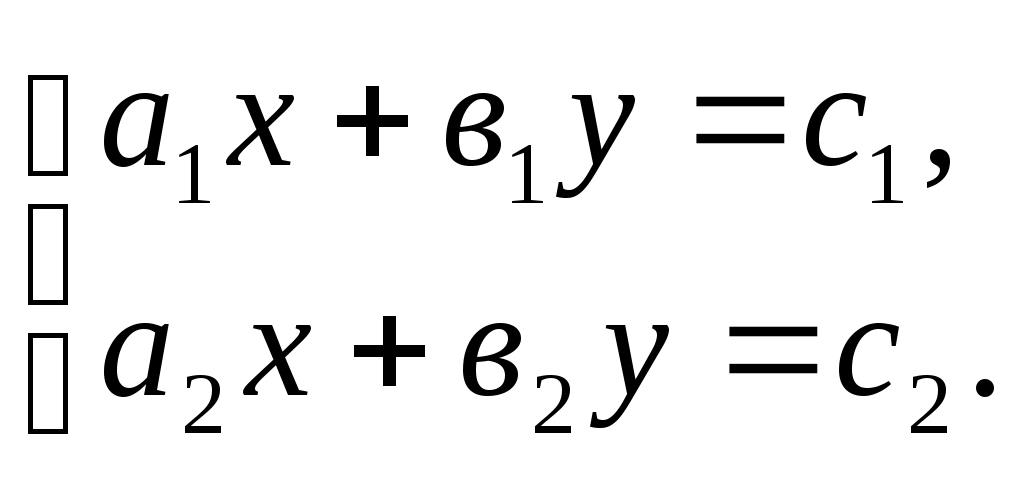 - Што называюць рашэннем сістэмы лінейных ураўненняў з дзвюма зменнымі? (упарадкаваная пара лікаў (х,у), якія пераўтвараюць кожнае ўраўненне сістэмы ў правільную лікавую роўнасць) - Якія дзве сістэмы ўраўненняў называюцца раўназначнымі? (калі рашэнне адной сістэмы з’яўляецца рашэннем другой) - Якія існуюць спосабы рашэння сістэм лінейных ураўненняў з дзвюма зменнымі? (аналітычны і графічны) - Назавіце аналітычныя спосабы рашэння сістэм ураўненняў? (спосаб складання , спосаб падстаноўкі) - У чым заключаецца графічны спосаб рашэння сістэм лінейных ураўненняў? (пабудаваннем графікаў лінейных функцый) - Пры якіх суадносінах паміж каэфіцыентамі а1,b1,с1,а2,b2,с2 сістэма лінейных ураўненняў 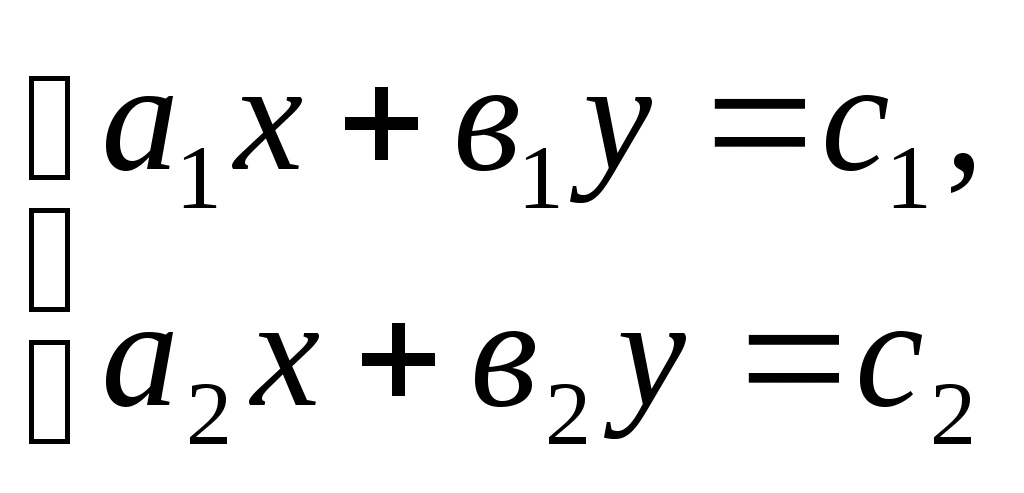 :а) мае адзіннае рашэнне;  б) мае бясконцае мноства рашэнняў;  в) не мае рашэнняў?  3) Вуснае лічэнне. 1. Назавіце ўсе пары натуральных лікаў, якія з’яўляюцца рашэннем ураўнення х+у=12. Колькі рашэнняў мае дадзенае ўраўненне? Ці можна паказаць усе пары цэлых лікаў, якія з’яўляюцца рашэннем дадзенага ўраўнення? 2. Ці праходзіць праз пункт М(0;3) прамыя х+у=3 і –х+2у=3? (праходзіць праз прамую х+у=3) 3. Пакажыце рашэнне сістэм ураўненняў: а)  (4;3) б)  (7;2)4. Для ўраўнення х-у=5 падбярыце такое ўраўненне першай ступені,каб з дадзеным ураўненнем утварылася сістэма, якая: а) мае адзінае рашэнне; б) мае бясконцае мноства рашэнняў; в) не мае рашэнняў. 5. Ці раўназначныя сістэмы ўраўненняў  і 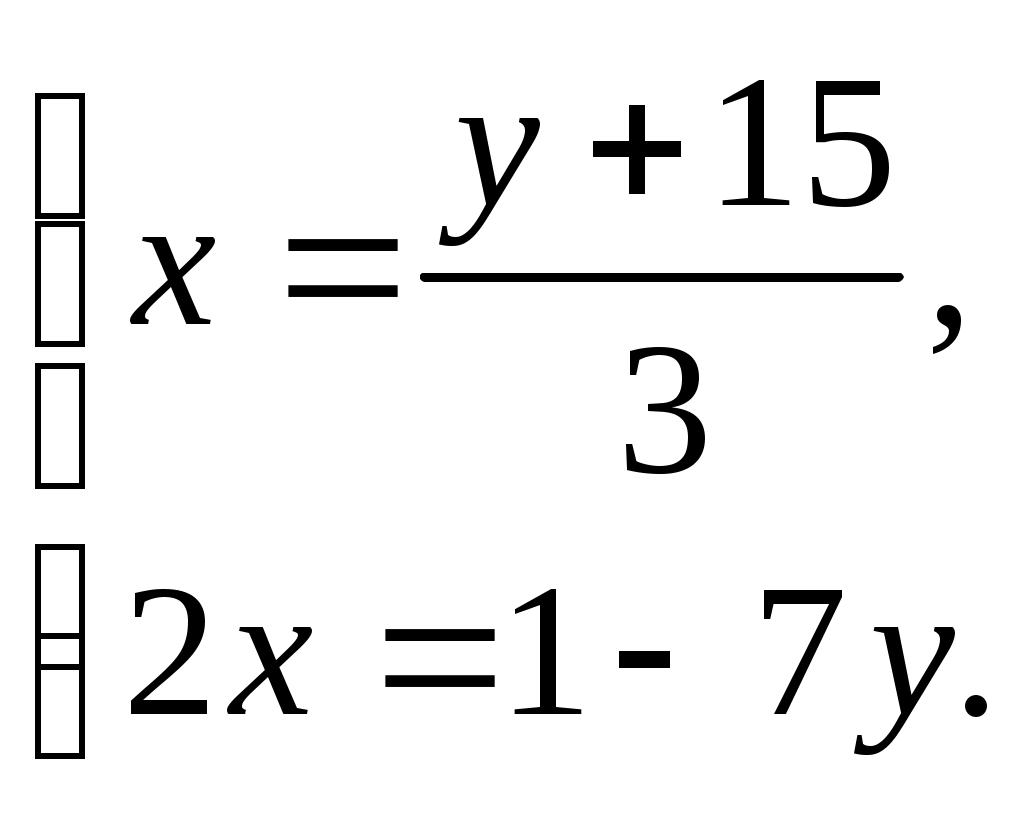 (так)4) Вуснае рашэнне. Карткі з заданнямі і табліца адказаў знаходзяцца на сталах у вучняў. а) Картка №1. Пакажыце прамыя, якія вызначаюцца ўраўненнямі сістэмы. Адказы: 1) Б; 2) Г; 3) Б. б) Картка №2. Пакажыце сістэму ўраўненняў, якая 1) ) не мае рашэнняў; (В) б) мае адзінае рашэнне; (В) в) мае бясконцае мноства рашэнняў; (Б) ІІІ. Фізкультхвілінка. ФХ для паляпшэння мазгавога кровазвароту: 1. Зыходнае становішча (з.с.) – седзячы на стуліку, 1-2 – адвесці галаву назад і плаўна нахіліць назад; 3-4 – галаву нахіліць наперад, плечы не падымаць. Паўтарыць 4-6 разы. Тэмп павольны. 2. З.с. - седзячы на стуле, рукі на поясе. 1 – паварот галавы направа; 2 – з.с.; 3 – паварот галавы налева; 4 – з.с. Паўтарыць 6-8 разоў. Тэмп павольны. Гімнастыка для вачэй: 1. З.с. – седзячы, адкінуўшыся на спінку стуліка. Прыкрыць павекі, крэпка зажмурыць вочы, потым адкрыць. Паўтарыць 4-6 разы. 2. З.с. – седзячы. Падняць вочы ўверх, зрабіць імі кругавыя рухі па часавой стрэлцы, потым супраць часавой стрэлкі. Паўтарыць 5-6 разоў. 3. З.с. – седзячы. Глядзець прама перад сабой на класную дошку 2-3 секунды, перавесці погляд на кончык носа на 3-5 секунды. Паўтарыць 6-8 разоў. ІV. Рашэнне тэставых заданняў (самастойна). Вучні выконваюць заданні і адказы заносяць у табліцу. Запоўніце табліцу:
Пасля выканання тэставых заданняў правяраецца іх правільнасць выканання лістамі-адказамі. V. Работа ў дошкі. Тэставае заданне. Няхай (х;у) – рашэнне сістэмы  Тады значэнне выразу 13∙(х-у) роўна 1) 18; 2) 40; 3) 108; 4) 2,6; 5) 3,6.Рашэнне. Для рашэння сістэмы прыменім спосаб складання:     + 3 ∙ + 2у = 5,13х = 29, 87 + 26у = 65, х =  26у = -22, у = -  = - .13∙(х-у) = 13 ∙  = 13 ∙ = 40.Адказ: 2. Рашыце самастойна: №7. Няхай (х;у) – рашэнне сістэмы 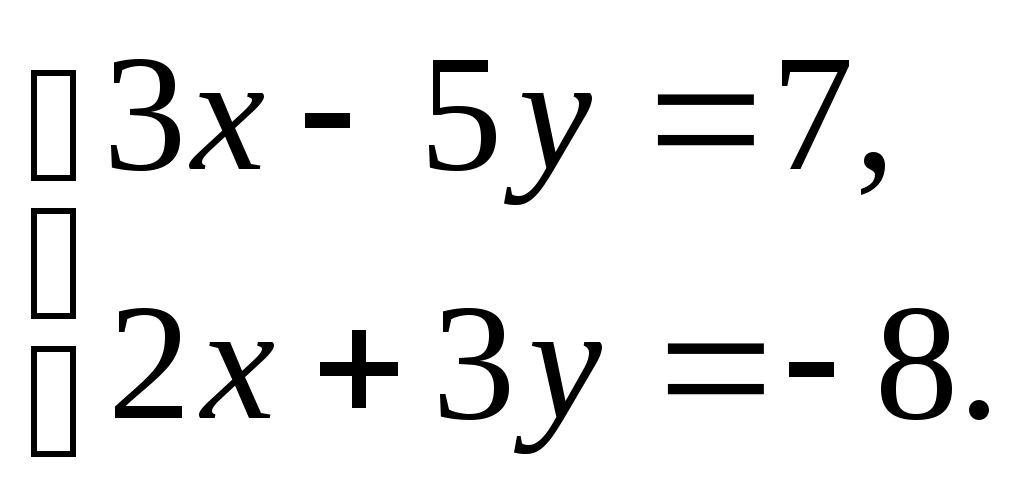 Тады сума х + у роўна 1) 0; 2) 4; 3) -4; 4) 3; 5) -3. Рашэнне. Для рашэння сістэмы прыменім спосаб складання:  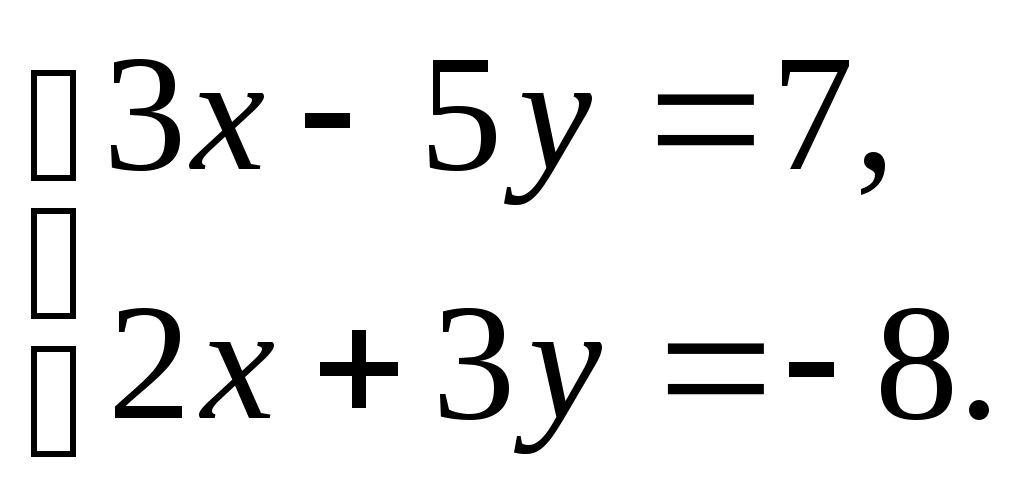  + 3х + 5∙2 = 7, 3х = -3, х = -1.-19у = 38, у =-2. х + у =-2 + (-1) = -3. Адказ: 5. Дадатковае заданне: (тэставае) Дадзен графік функцыі у = kx + b. Сума k + b роўна  1) 3 ; 2) -2; 3) - ; 4) 8; 5) 2 . (Рэп. 1,2этапы 2008/2009г.)Рашэнне. Прамая перасякае восі каардынат у пунктах (5;0), (0;3). Саставім сістэму ўраўненняў      Сума k + b = -0,6 + 3 = 2,4 = 2 .Адказ: 5. Рашыце самастойна: №8. (тэставае) Дадзен графік функцыі у = kx + b. Сума k + b роўна  1) 4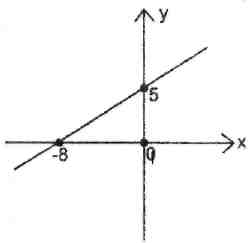 ; 2) 5 ; 3) -3; 4) 2 ; 5) - . (Рэп. 1,2этапы 2008/2009г.) Рашэнне.Прамая перасякае восі каардынат у пунктах (-8;0), (0;5). Саставім сістэму ўраўненняў      Сума k + b = 5 + =5 .Адказ: 2. VI. Дамашняе заданне (дыферанцыравана, па картках). VII. Рэфлексія. Падвядзенне вынікаў урока. Сёння на ўроку мы абагульнілі веды па рашэнню сістэм лінейных ураўненняў, замацавалі іх пры выкананні тэставых заданняў і кожны з вас зрабіў самаацэнку сваёй працы на ўроку, ацэнку сваіх ведаў па дадзенай тэме і вывеў некаторыя вынікі для сябе. Урок я хачу закончыць словамі: "Музыка может возвышать или умиротворять душу, Живопись - радовать глаз, Поэзия - пробуждать чувства, Философия - удовлетворять потребности разума, Инженерное дело - совершенствовать материальную сторону жизни людей, а математика способна достичь всех этих целей". Так сказаў амерыканскі матэматык Морыс Клайн. Дзякуй за працу на ўроку! Дамашнія заданні Варыянт 1. (ІІ узровень) 1.Рашыце метадам падстаноўкі сістэму ўраўненняў:  2.Рашыце сістэму ўраўненняў метадам складання:  3.Ці з’яўляецца рашэннем сістэмы ўраўненняў  пара лікаў (-1;4).Варыянт 2. (ІІІ узровень) 1.Рашыце метадам падстаноўкі сістэму ўраўненняў:  2.Рашыце сістэму ўраўненняў метадам складання: 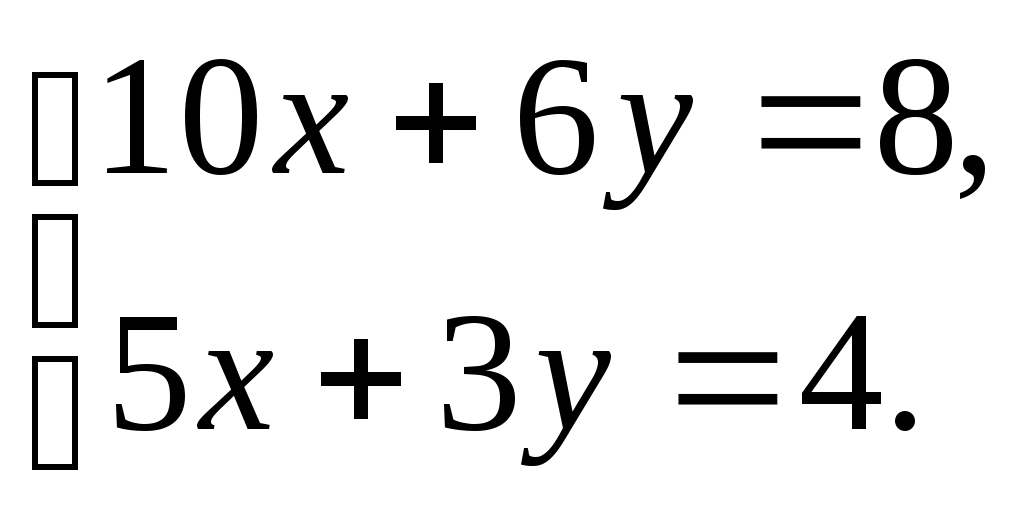 3. Прамая у = kх + b праходзіць праз пункты А(1;2) і В(2;-1). Знайдзіце k і b. Варыянт 3. (ІV узровень) 1.Рашыце сістэму ўраўненняў  2. Выбярыце ўраўненне, графік якога паказан на рысунку.  1) у – х = 2; 2) у + х = 2; 3) х – у = 2; 4) х + у = - 2; 5) 2х - 2у = 2. (РЦ 2 этап, 2007/2008 н.г.) Літаратура: 1. А.П.Кузняцова, Г.Л.Мураўёва. Алгебра. Вучэбны дапаможнік для 9 класа. 2-е выданне – Мінск “Народная асвета”, 2006. 1. К.А.Ананчанка, М.Ц.Вараб’ёў. Алгебра. Падручнік для 9 класа агульнаадукацыйнай школы з паглыбленным вывучэннем матэматыкі. 2-е выданне – Мінск “Народная асвета”, 1999 3. Дидактические материалы по алгебре: 9 класс: самостоятельные и контрольные работы / К.О.Ананченко, И.Н.Ринейский. – Минск: Аверсэв, 2008. – 188с. 4. А.П.Кузняцова, Г.Л.Мураўёва. Алгебра. Самастойныя і кантрольныя работы. Тэсты. Дапаможнік для настаўнікаў. – Мінск “Народная асвета”, 2005. 5. В.В.Веременюк, В.В.Кожушко Практикум по математике: подготовка к тестированию и экзамену – Мн.: ТетраСистемс, 2005. – 160с. 6. Заданні РЦ 2006-2009 н.г. І. Пакажыце прамыя, якія вызначаюцца ўраўненнямі сістэмы   Адказы на тэсты
Адказы на тэсты
- - |