|
|
Технологическая карта урока по геометрии на тему: Параллельный перенос. технологическая карта урока по геометрии параллельный перенос. Урока Тема урока Параллельный перенос Класс 8 Предмет геометрия
Технологическая карта урока
Тема урока: Параллельный перенос
Класс: 8
Предмет: геометрия
УМК: Геометрия. 8 класс / Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, И.И. Юдина
Тип урока: урок закрепление
Планируемые результаты обучения:
Личностные:
Развитие навыка самостоятельности в работе, трудолюбия, аккуратности, развитие навыков самоанализа и самоконтроля при оценке результата и процесса своей деятельности.
Метапредметные:
Формирование информационной, коммуникативной и учебной компетентности учащихся, умения работать с имеющейся информацией в новой ситуации.
Предметные:
Формирование навыка употребления термина «параллельный перенос».
Цели урока:
Образовательная цель: закрепление знаний о параллельном переносе, а так же знаний о выполнении параллельного переноса и их применение при решении задач.
Задачи:
закрепить понятие параллельного переноса;
закрепить полученные знания о выполнении построений параллельного переноса на практике;
сформировать умение решать задачи с применением знаний о параллельном переносе.
Развивающая цель: развитие логического мышления, памяти, математической речи, умение доказательно развивать свою мысль и умение делать выводы.
Задачи:
развивать память учащихся при повторении пройденного материала;
развивать познавательный интерес при решении задач разной направленности;
развивать умение преодолевать трудности при решении математических задач;
развивать умение делать выводы при решении задач на доказательство.
Воспитательная цель: воспитание нравственных качеств личности учащихся.
Задачи:
воспитать чувства уважительного отношения к ответам одноклассников;
требовать соблюдения аккуратности ведения записей в тетради, дисциплины в классе.
Методы обучения: активный, практический, частично-поисковый.
Средства обучения: учебник геометрии 7-9 классов Л.С. Атанасяна, карточки с домашним заданием.
|
Этапы урока
|
Деятельность учителя
|
Деятельность учащихся
|
УУД
|
|
|
1.Организационный момент
|
Здравствуйте, ребята! Присаживайтесь. Кирилл, кто сегодня отсутствует на уроке?
|
Приветствуют учителя. Кирилл называет отсутствующих.
|
Самоорганизация.
|
|
|
2. Проверка домашнего задания
|
Ребята, с какой темой вы познакомились на прошлом уроке? Витя, пожалуйста.
Всё верно.
Давайте вспомним, что же такое параллельный перенос на вектор?
Катя, пожалуйста.
Правильно, умница!
Ответьте на вопрос, является ли параллельный перенос движением? Саша, пожалуйста!
Молодец, верно!
Назовите, пожалуйста, основные свойства, которыми обладает параллельный перенос, Оля?
Спасибо, Оля.
Продолжи, во что переходят параллельные прямые, перпендикулярные прямые, Максим?
Хорошо!
Итак, вы повторили теоретические аспекты, и мне бы хотелось, чтобы вы сегодня на уроке научились применять их на практике, а именно, при решении задач.
Ребята, откройте тетради, запишите число и тему урока: «Параллельный перенос. Решение задач».
Обратите внимание на доску. На доске представлена точка 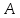 , отрезок , отрезок 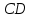 и вектор и вектор 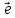 . Начертите у себя в тетрадях данные геометрические объекты. . Начертите у себя в тетрадях данные геометрические объекты.
Задание: «Постройте точку 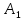 , отрезок , отрезок 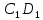 , которые получаются из точки , которые получаются из точки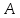 и отрезка и отрезка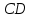 , соответственно, параллельным переносом на вектор , соответственно, параллельным переносом на вектор 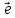 . .
Итак, закончили выполнять задание.
Поменяйтесь тетрадями в парах.
Расскажите, по какому принципу вы строил точку 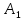 , Олег? , Олег?
Молодец, всё верно.
А как Вы построили отрезок 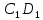 , Ксюша? , Ксюша?
Замечательно, Ксюша.
Даю минуту на исправление ошибок, можете в парах помочь друг другу.
Если есть вопросы по выполнению задания, поднимите руку.
|
Витя: «Параллельный перенос».
Катя: «Параллельным переносом на вектор 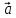 называется отображение плоскости на себя, при котором каждая точка называется отображение плоскости на себя, при котором каждая точка 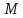 отображается в такую точку отображается в такую точку 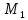 , что вектор , что вектор 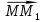 равен вектору равен вектору 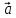 ». ».
Саша: «Да, параллельный перенос является движение, поскольку плоскость отображается на себя, сохраняя расстояния».
Оля: «Параллельный перенос является движением, при данном преобразовании отрезок переходит в равный ему отрезок, угол переходит в равный ему угол, окружность переходит в равную ей окружность и любой многоугольник переходит в равный ему многоугольник».
Максим: «Параллельные прямые переходят в параллельные прямые, перпендикулярные прямые переходят в перпендикулярные прямые».
Записывают тему урока в тетрадях: «Параллельный перенос. Решение задач».
Чертят в тетрадях точку, прямую, отрезок и вектор.
Выполняют задание.
По завершении выполнения задания меняются тетрадями в парах.
Олег: «Чтобы построить точку 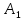 , необходимо от точки , необходимо от точки 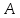 отложить вектор, равный вектору отложить вектор, равный вектору 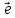 . Точка . Точка 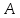 переходит в точку переходит в точку 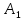 . Точка . Точка 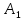 – искомая». – искомая».
Ксюша: «Чтобы построить отрезок 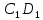 , сначала нужно от точки , сначала нужно от точки 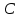 отложить вектор, равный вектору отложить вектор, равный вектору 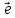 . Затем от точки . Затем от точки 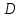 отложить вектор, равный вектору отложить вектор, равный вектору 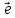 . Точка . Точка 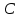 переходит в точку переходит в точку 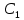 , точка , точка 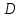 – в точку – в точку 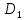 . Соединяем полученные точки. Отрезок . Соединяем полученные точки. Отрезок 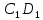 – искомый». – искомый».
|
Познавательные: применение предметных знаний; выполнение учебных заданий.
Регулятивные: выделение и осознание того, что уже пройдено. Постановка учебной задачи на основе известного.
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог.
Личностные: самоопределение.
Коммуникативные: развитие умения интегрироваться в группу сверстников и строить продуктивное взаимодействие
|
|
4. Закрепление изученного материала
|
Итак, вы вспомнили определение параллельного переноса, его основные свойства, а так же повторили, как построить точку и отрезок параллельным переносом на заданный вектор. Теперь можем приступить к решению задач.
Откройте учебник на странице 302, номер задачи 1164. К доске пойдет Кирилл.
Кирилл, прочитай условие задачи. Ты выполняешь задание под буквой а).
О чем говорится в задаче?
Как расположена точка 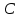 относительно точки относительно точки 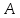 и и 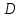 ? ?
Верно.
Запишите условие задачи, постройте чертеж.
Предлагаю обозначить вектор 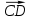 . .
Кирилл, как ты думаешь, что необходимо сделать, что бы построить точку 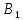 ? ?
Спасибо, Кирилл, всё верно, молодец! Присаживайся.
Под буквой б) задание выполнит Лёша, выходи к доске.
Что нам нужно доказать, чтобы фигура 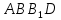 являлась трапецией? являлась трапецией?
Хорошо, а как доказать, что полученная трапеция является равнобедренной?
Верно, что ты можешь сказать об отрезках 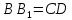 ? ?
Хорошо, а об отрезках 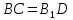 ? ?
Какой вывод можно сделать?
Верно. По условию дан равнобедренный треугольник, значит, что можно сказать о его боковых сторонах?
Да, теперь посмотри на 3 и 6 пункт, что ты можешь сказать?
Если 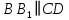 , то как будут расположены отрезки , то как будут расположены отрезки 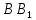 и и 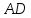 ? ?
Какой вывод можно сделать из пунктов 1, 2 и 8?
Хорошо, а теперь посмотри на все пункты доказательства и сделай заключительный вывод.
Молодец, Лёша, цель достигнута, присаживайся на место.
А сейчас обсудим задачу под номером 1178 на странице 304, которая будет являться вашим домашним заданием.
Саша, прочитай условие задачи.
Ответьте, о каких геометрических фигурах говориться в задачи, Катя?
Что требуется оказать в задаче, Данил?
Рассмотрите чертёж, что вы можете сказать о сторонах квадратов 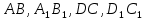 , Вера? , Вера?
Хорошо, а теперь обратите внимание на диагонали квадратов 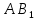 и и 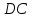 . Как они расположены по отношению друг к другу, Миша? . Как они расположены по отношению друг к другу, Миша?
А что ты можешь тогда сказать о половинах этих диагоналей 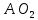 и и 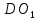 ? ?
Верно, вы уже устно доказали, что 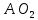 и и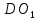 параллельны и равны, а в задаче требуется доказать, что параллельны и равны, а в задаче требуется доказать, что 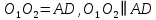 , значит какую фигуру можно рассмотреть, Женя, назови? , значит какую фигуру можно рассмотреть, Женя, назови?
Делаю вам подсказку: если вы докажите, что фигура 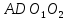 – параллелограмм, то задача будет решена. Дома вы подумаете над доказательством и оформлением доказательства. – параллелограмм, то задача будет решена. Дома вы подумаете над доказательством и оформлением доказательства.
|
Открывают учебник.
Кирилл: «Даны равнобедренный треугольник 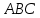 с основанием с основанием 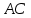 и точка и точка 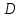 на прямой на прямой 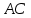 , такая, что точка , такая, что точка 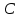 лежит на отрезке лежит на отрезке 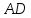 . .
а) Постройте отрезок 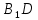 , который получается из отрезка , который получается из отрезка 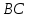 параллельным переносом на вектор параллельным переносом на вектор 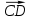 . б) Докажите, что четырехугольник . б) Докажите, что четырехугольник 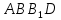 – равнобедренная трапеция». – равнобедренная трапеция».
Кирилл: «О равнобедренном треугольнике. Точка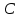 лежит между точками лежит между точками 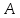 и и 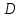 ». ».
Кирилл: «Дано:
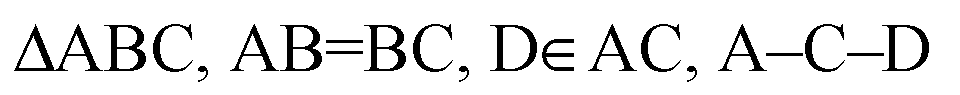
а) построить: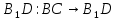 при перенос на при перенос на 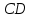 . .
Построение:
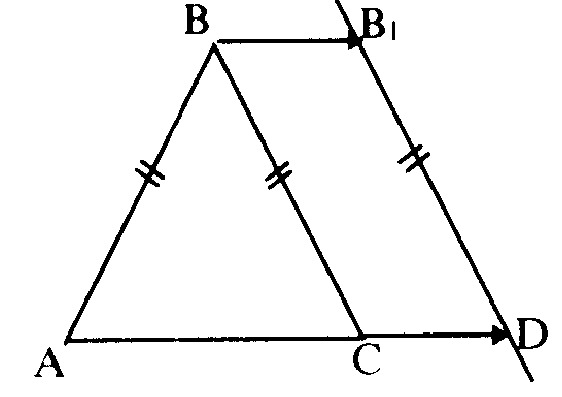
1. От точки 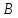 отложим вектор отложим вектор 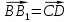 ; ;
2. Соединим точку 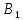 и и 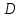
3. 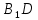 – искомый». – искомый».
Лёша: «Доказать: 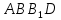 – равнобедренная трапеция. – равнобедренная трапеция.
Чтобы доказать, что фигура 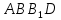 – трапеция, необходимо доказать, что – трапеция, необходимо доказать, что
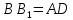 . .
Для этого нужно доказать, что 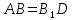 . .
1. 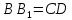 (по построению). (по построению).
2. 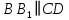 (по определению параллельного переноса). (по определению параллельного переноса).
3. 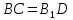 (по свойству параллельного переноса). (по свойству параллельного переноса).
4. 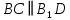 (по определению параллельного переноса). (по определению параллельного переноса).
5. Из (1), (2), (3), (4) – 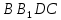 – параллелограмм (по определению параллелограмма). – параллелограмм (по определению параллелограмма).
Что и требовалось доказать».
6. 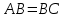 (по условию). (по условию).
7. Из (3), (6) – 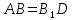 . .
8. 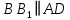 (по построению). (по построению).
9. Из (1), (2), (8) – 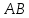 не параллелен не параллелен 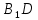 . .
10. Из (7), (8), (9) – 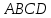 – равнобедренная трапеция. – равнобедренная трапеция.
Что и требовалось доказать».
Саша: «На сторонах 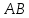 и и 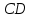 параллелограмма параллелограмма 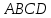 построены квадраты так, как показано на рисунке 332. Используя параллельный перенос, докажите, что отрезок, соединяющий центры этих квадратов, равен и параллелен стороне построены квадраты так, как показано на рисунке 332. Используя параллельный перенос, докажите, что отрезок, соединяющий центры этих квадратов, равен и параллелен стороне 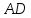 ». ».
Катя: «В задачи говориться о двух квадратах 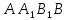 и и 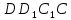 , а так же о параллелограмме , а так же о параллелограмме 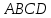 ». ».
Данил: «Доказать: 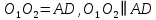 ». ».
Вера: «Данные стороны равны и параллельны по построению, поскольку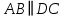 по условию». по условию».
Миша: «Диагонали расположены параллельно.
Диагонали так же будут равны друг другу и параллельны».
Женя: «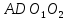 ». ».
|
Познавательные: извлечение из текстов математической информации, структурирование знаний, выбор способов решения задач, анализ объектов и синтез.
Построение логической цепи рассуждений.
Регулятивные: планирование пути достижения цели; прогнозирование.
Коммуникативные: развитие умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействия.
Личностные: осознание ответственности за общее дело.
Познавательные: осознанное и произвольное построение речевого высказывания.
Коммуникативные: выражение своих мыслей с достаточной полнотой и точностью, формирование и аргументация своего мнения в коммуникации.
|
|
5. Постановка домашнего задания
|
Наш урок подходит к концу. Открываем дневники, записываем домашнее задание. Учебник, номер 1178 на странице 304. Вам необходимо будет перенести чертеж в тетрадь, оформить доказательство задачи. А так же письменно выполнить задание на карточках.
Принести на следующий урок транспортир и циркуль.
У кого есть вопросы, как выполнять домашнее задание, поднимите руку?
Хорошо.
|
Записывают домашнее задание в дневники. Получают карточки.
|
|
|
6. Подведение итогов урока
|
Ребята, чему вы сегодня научились на уроке?
Сегодня вы закрепили знания о понятии параллельного переноса, а так же отработали на практике навыки построения геометрических фигур по средством параллельного переноса.
Ребята, продолжите фразы:
«Сегодня на уроке я повторил…»
«Сегодня на уроке я узнал…»
Хорошо!
На сегодняшнем уроке вы хорошо поработали.
Поставлю оценки тем, кто выходил к доске и отвечал с места. Кирилл получает 5, Лёша – 5 … и т.д.
На этом наш урок окончен. Всем спасибо за урок!
До свидания!
|
Решать задачи с использованием такого преобразования, как параллельный перенос.
Сегодня на уроке я повторил, как строить геометрические фигуры по средством параллельного переноса.
Сегодня на уроке я узнал, что параллельный перенос можно применять при решении задач.
До свидания!
|
Личностные: формирование навыков анализа, самоанализа и активности. Формирование умения нравственно-этического оценивания.
Коммуникативные: адекватно отображать свои чувства, мысли в речевом высказывании.
|
|
|
|
 Скачать 36.85 Kb.
Скачать 36.85 Kb.
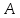 , отрезок
, отрезок 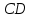 и вектор
и вектор 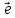 . Начертите у себя в тетрадях данные геометрические объекты.
. Начертите у себя в тетрадях данные геометрические объекты.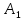 , отрезок
, отрезок 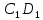 , которые получаются из точки
, которые получаются из точки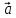 называется отображение плоскости на себя, при котором каждая точка
называется отображение плоскости на себя, при котором каждая точка 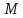 отображается в такую точку
отображается в такую точку 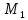 , что вектор
, что вектор 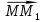 равен вектору
равен вектору 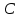 отложить вектор, равный вектору
отложить вектор, равный вектору 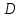 отложить вектор, равный вектору
отложить вектор, равный вектору 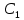 , точка
, точка 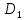 . Соединяем полученные точки. Отрезок
. Соединяем полученные точки. Отрезок 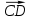 .
.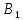 ?
?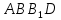 являлась трапецией?
являлась трапецией?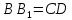 ?
?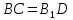 ?
?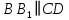 , то как будут расположены отрезки
, то как будут расположены отрезки 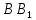 и
и 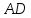 ?
?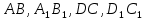 , Вера?
, Вера?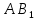 и
и 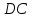 . Как они расположены по отношению друг к другу, Миша?
. Как они расположены по отношению друг к другу, Миша?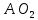 и
и 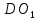 ?
?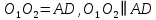 , значит какую фигуру можно рассмотреть, Женя, назови?
, значит какую фигуру можно рассмотреть, Женя, назови?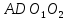 – параллелограмм, то задача будет решена. Дома вы подумаете над доказательством и оформлением доказательства.
– параллелограмм, то задача будет решена. Дома вы подумаете над доказательством и оформлением доказательства.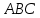 с основанием
с основанием 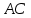 и точка
и точка 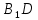 , который получается из отрезка
, который получается из отрезка 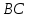 параллельным переносом на вектор
параллельным переносом на вектор 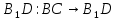 при перенос на
при перенос на 
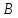 отложим вектор
отложим вектор 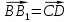 ;
;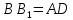 .
.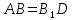 .
.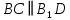 (по определению параллельного переноса).
(по определению параллельного переноса).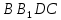 – параллелограмм (по определению параллелограмма).
– параллелограмм (по определению параллелограмма).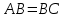 (по условию).
(по условию).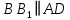 (по построению).
(по построению).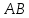 не параллелен
не параллелен 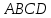 – равнобедренная трапеция.
– равнобедренная трапеция. 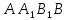 и
и 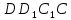 , а так же о параллелограмме
, а так же о параллелограмме 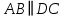 по условию».
по условию».