решение задач по теме смежные и вертикальные углы. Урок по геометрии в 7 классе.. Решение задач по теме Смежные и вертикальные углы
 Скачать 99 Kb.
|
|
Урок по геометрии в 7 классе. Решение задач по теме «Смежные и вертикальные углы». Федотова Татьяна Валентиновна, учитель математики. Тип урока: урок закрепления нового материала Цели урока: Образовательные: повторить и закрепить понятия о смежных и вертикальных углах; Развивающие: развивать умение анализировать условие задачи; Воспитательные: воспитание аккуратности (аккуратное выполнение чертежей на доске и в тетрадях, рациональное распределение записей). Структура урока: I этап. Организационный момент II этап. Актуализация опорных знаний III этап. Закрепление изученного материала IV этап. Зарядка для глаз V этап. Самостоятельная работа VI этап. Домашнее задание VII этап. Итог урока ХОД УРОКА I. Организационный момент Приветствие, сообщение темы, целей и задач. Учитель: Вам было задано домашнее задание: повторить п.14 и 15, ответить на вопросы 1, 2,3,6,7. Сейчас проверим, как вы подготовились к уроку. II. Актуализация опорных знаний Вопрос: Какие углы называются смежными? ( Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными полупрямыми)  В А О С Вопрос. Из рисунка назвать смежные углы. (Ответ: ∠ АОВ и ∠ВОС – смежные углы) Вопрос. Какая сторона у них общая? (Ответ: ОВ- общая сторона.) Вопрос. Назвать дополнительные полупрямые. (Ответ. ОС и ОА - дополнительные полупрямые.) В  опрос. Какими свойствами обладают смежные углы? Ответ. -  Сумма смежных углов равна 180°(теорема) 1 2∠1 + ∠2 = 180° -Если два угла равны, то и смежные с ними углы равны. - Если угол не развернутый, то его градусная мера меньше 180°. -Угол, смежный с прямым, есть прямой угол. Вопросы. Могут ли два смежных угла быть равными: а) 75° и 80°; Ответ: (нет, т.к.75° + 80°=155°) б) 94° и 96°; Ответ: (нет, т.к. 94° + 96°= 190°) в) 83° и 97°? Ответ: ( да, т.к. 83° + 97°= 180°) Устно. Д     ано: Доказательство. О∠АОВ 3 1. ∠3 смежный с ∠1, а ∩ АО А 1 ∠4 смежный с ∠2 . а ∩ ОВ 2 2. Т.к. ∠3 = ∠4 ( по условию), ∠  3 = ∠4 4 то ∠1 = ∠ 2, как углы,Доказать смежные равным углам. ∠1 = ∠2 ( по свойству смежных углов). Вопрос. Какие углы называются вертикальными? (Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого).   а 2 b₁ ∠ 1 и ∠ 3 - вертикальные углы 1 3 ∠ 2 и ∠ 4 – вертикальные углы b 4 а₁ Вопрос. Каким свойством обладают смежные углы? Ответ. Вертикальные углы равны. (теорема)   ∠ 1 = ∠ 32 ∠ 2 = ∠ 4 1 3 4 III этап. Закрепление изученного материала. Решение задач. №  3(учебник) Д  ано: Решение.∠  1 и ∠2- смежные 1 2∠  1 больше ∠2 в 2 раза 1. Пусть ∠2 = х, тогда ∠1=2хНайти ∠1 и ∠2 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 2х = 180° 3х = 180°, ⇒ х =180°: 3, х = 60°. 3.Следовательно: ∠2 = 60°, ∠1 = 2∙60°= 120° Ответ: ∠1= 120°, ∠2= 60° №6(2) Д   ано: Решение.∠1 и ∠2 – смежные ∠   1 : ∠2 = 3 : 7 1 2Найти ∠1 и ∠2 1. Пусть х. – коэффициент пропорциональности. Тогда ∠1 = 3х, ∠2 = 7х (по условию задачи) 2. Т.к ∠1 + ∠2 = 180°( по теореме о смежных углах), то 3х + 7х = 180°, 10х = 180°, х = 18°. 3. Следовательно: ∠1 =3 ∙ 18°=54°, ∠2 =7 ∙ 18°=126° Ответ: 54°; 126°. Д  ано: Решение∠  1 и ∠2 - смежные 1 2 ∠ 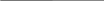 2 составляет 0,2 от∠1 Найти ∠1 и ∠2 1. Пусть ∠1 = х, тогда ∠2 = 0,2х ( по условию). 2. Т.к. ∠1 + ∠2 = 180°(по теореме о смежных углах), то х + 0,2х =180°, 1,2х = 180°, х = 150°, 3. Следовательно: ∠1=150°, ∠2= 0,2∙ 150°= 30°. Ответ: 150°, 30° Д  ано: Решение а ∩ b 2 а ∠  2 меньше ∠1 в 4 раза 1 3Найти ∠1, ∠2, ∠3 и ∠4 4 b 1.Пусть ∠2 = х , тогда ∠1 = 4х (по условию), 2. Т.к. ∠1+ ∠2 = 180° (по теореме о смежных углах), то 4х + х = 180°, 5х = 180°, х = 36°. 3.Следовательно: ∠2 = 36°, ∠1 = 4∙36° = 144° ∠3= ∠1, ∠4= ∠2( по теореме о вертикальных углах), значит ∠3= 144°, ∠4=36°. Ответ: 144°, 36°, 144°, 36°. Д  ано: Решение A   С ∩ ВD = O А В∠  ВОС = 23° О 23° Найти: ∠СОD, D С ∠АОВ, ∠АОD. 1. ∠АОD = ∠ВОС = 23° (по теореме о вертикальных углах) 2. ∠АОВ + ∠ВОС = 180° (по теореме о смежных углах). Следовательно: ∠АОВ =180°- ∠ВОС, т.е. ∠АОВ =180° - 23° = 157° 3. ∠СОD = ∠АОВ = 157° ( по теореме о вертикальных углах). Ответ: 157°, 157°, 23°. Устно. Вопрос. Назовите смежные и вертикальные углы.  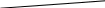    А DО  NM Ответ. Смежные углы:∠ АОМ и ∠ АОD, ∠АОD и ∠NОD, ∠NОD и ∠NОМ, ∠NОМ и ∠АОМ . Вертикальные углы: ∠АОМ и ∠NОD, ∠АОD и ∠NОМ. IV этап. Зарядка для глаз 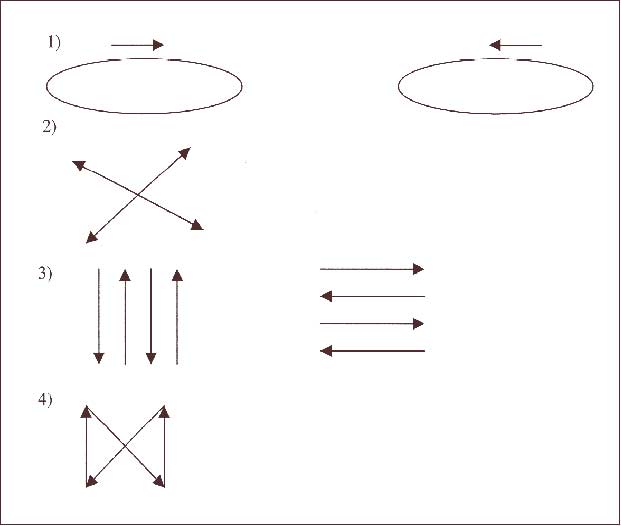 V этап. Самостоятельная работа ( на листочках)
Ответы
VI этап. Домашнее задание. 1) §2. Пункты 14-15. 2) Задачи на стр. 26. № 6(4), № 12. VII этап. Итог урока. Повторили понятия смежных и вертикальных углов Научились решать задачи, используя знания о смежных и вертикальных углах. Стали еще на одну ступеньку выше в изучении геометрии. |