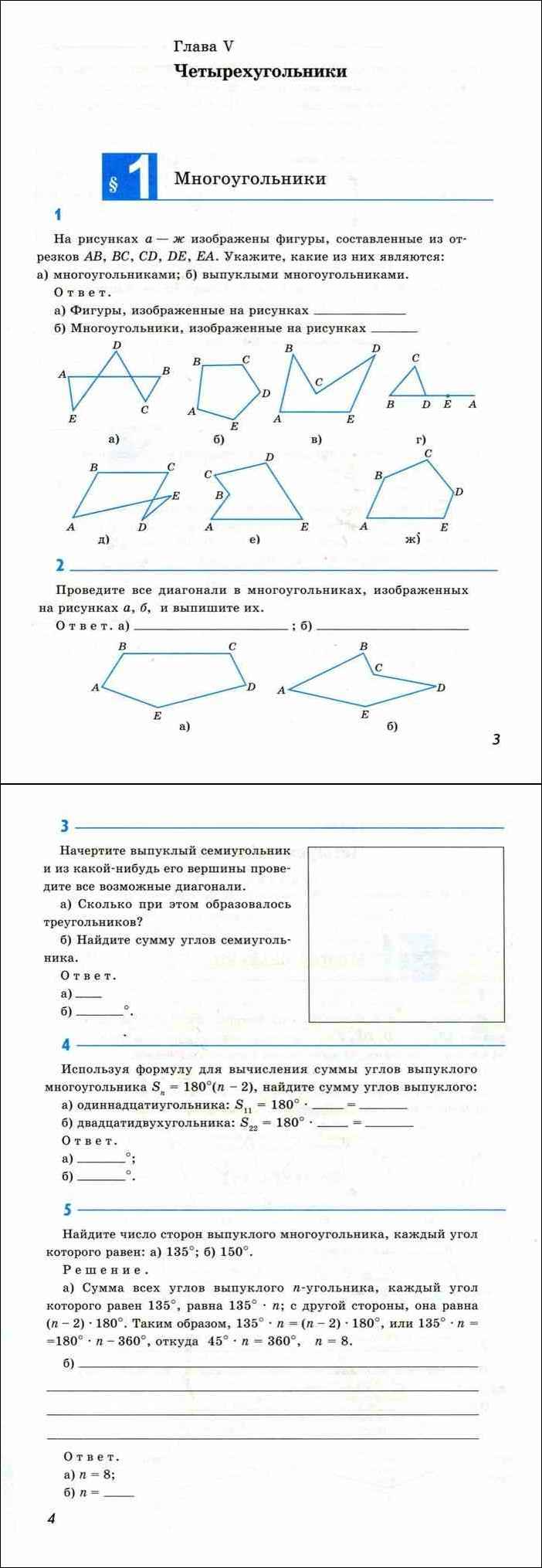
Этапы урока
|
№ слайда
|
Деятельность учителя
|
Организационный момент
|
№1
|
- Приветствует обучающихся, настраивает на работу.
- Предлагает проверить готовность рабочего места.
- Сообщает тему урока.
|
Актуализация знаний. Постановка проблемы
|
№2
|

- Проводит фронтальный опрос по чертежу на слайде.
- Что общего у фигур изображённых на экране?
|
Изучение нового материала и его первичное закрепление
|
№3
|
Даёт задание:
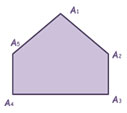
- Нарисуйте в тетради фигуру, изображённую на экране.
- Назовите отрезки, из которых состоит данная фигура.
- Названные вами отрезки можно разделить на смежные и несмежные.
|
№4
|
- Учитель формулирует определение смежных отрезков: cмежными называются отрезки, соединяющие соседние вершины фигуры.
- Запишите в тетради название двух смежных отрезков.
- Попробуйте сформулировать определение “несмежный” отрезок.
- Запишите в тетради название двух несмежных отрезков
|
№5
|
Учитель формулирует определение:Многоугольник - это фигура, состоящая из отрезков, причём смежные отрезки не лежат на одной прямой, а несмежные отрезки не пересекаются.
- Найдите в учебнике это определение и прочитайте его ещё раз про себя.
- Найдите в учебнике на стр. 98 рис. 150,151,152 и ответьте на следующие вопросы:
- Назовите многоугольники, изображённые на данных рисунках.
- Почему фигуру, изображённую на рис. 152 нельзя назвать многоугольником?
|
№6
|
- Запишите отрезки, из которых состоит многоугольник, нарисованный в тетради.
- Они называются сторонами многоугольника.
- Вспомните, что называется периметром треугольника, квадрата, прямоугольника.
- Учитель обобщает:
Периметром многоугольника называется сумма длин его сторон.
|
№7
|
- Соедините две несмежные вершины отрезком.
- Формулирует определение: отрезок, соединяющий две любые несоседние вершины многоугольника, называется диагональю.
- Проведите все диагонали многоугольника.
|
№8
|
- Около многоугольника нарисуйте “облачко” - образ плоскости.
- Формулирует определение внутренней и внешней области многоугольника.
- Формулирует ещё одно определение “многоугольника”: многоугольником называется фигура, состоящая из отрезков и внутренней области.
|
№9
|
- Информирует о том, что многоугольники бывают выпуклые и невыпуклые.
- Даёт определение: многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через любые две соседние вершины.
Многоугольник называется невыпуклым, если он лежит по разные стороны от хотя бы одной прямой, проходящей через две соседние вершины.
|
|
- В рабочей тетради выполните задания №1 и №2.
|
№10
|
- Нарисуйте в тетради выпуклый и невыпуклый многоугольники.
|
№11
|
- Нарисуйте четырёхугольник, пятиугольник и шестиугольник.
- Проведите в них диагонали, исходящие из одной вершины.
- Сколько треугольников образовалось в каждой фигуре?
|
№12
|
- Чему равна сумма углов в каждом многоугольнике?
|
|
- В рабочей тетради выполните задания №3.
|
№13
|
- Нарисуйте произвольный выпуклый n- угольник.
- Вопросы к классу:
- Сколько сторон в этом многоугольнике?
- Сколько образуется треугольников, если в нём провести диагонали, выходящие из одной вершины?
- Чему равна сумма углов в этом n- угольнике?
|
Самостоятельная работа с последующей проверкой
|
№14
|
- Выполните самостоятельно №364 из учебника
|
|
- В рабочей тетради выполните задания №4,5.
- Разберите по рабочей тетради выполнение задания №5 под буквой а) и выполните задание №5 б – самостоятельно.
|
Итог урока
|
№15
|
Подводит итоги урока.
Задает задание на дом.
|
 Скачать 115.07 Kb.
Скачать 115.07 Kb.