степень числа конспект урока. Уроки по теме "Решение дробных рациональных уравнений"
 Скачать 287.5 Kb.
|
1 2 Цели урока: Обучающие: Сформировать умения выполнять арифметические действия с числами, записанные в стандартном виде, и преобразовывать рациональные выражения, записанные с помощью степени с целым показателем. Развивающие: развитие логического и математического мышления, развитие творческой деятельности. Воспитательные: развитие личностных качеств. Ход урока. 1. Организационный момент. Ну-ка проверь, дружок, Ты готов начать урок? Все ль на месте, Все ль в порядке- Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят? Тут затеи и задачи, Игры, шутки – все для вас! Пожелаю всем удачи. За работу, в добрый час! 2. Мотивация урока. Сегодняшний урок мне хочется начать с цитаты Константина Эдуардовича Циолковского - основоположника космонавтики. «Сначала я делал открытия известные всем, затем известные не многим, а потом никому не известные». Вот и мы сегодня решим несколько известных вам задач, а затем, я думаю, вы сами научитесь составлять свои задачи. Но в начале проверим знания по теме степень с целым показателем. 3. Актуализация изучения темы. Проверка д/з. 1. Дайте определение степени с натуральным показателем. 2. Дайте определение степени с целым отрицательным показателем. 3. Чему равна нулевая степень любого отличного от нуля числа? 4. Как называется число, которое возводим в степень? 5. Как называется число, в которое возводим степень? 6. Какое число получаем при возведении в степень положительного числа? 7. Какое число получаем при возведении отрицательного числа с четным показателем? 8. Какое число получаем при возведении отрицательного числа с нечетным показателем? Проверьте, верно, ли выполнено действие. Если неверно, исправьте ошибку. 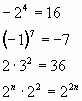 Вычислите: а) 3,2 * 10; б) 0,032 * 100; в) 0,032*1000; г) 32,3 : 10; д) 32,3 : 100; е) 32,3 : 1000. Решить № 242. 4. Изучение нового материала. Старт от английского слова (standard). Стандарт, это образец эталон, с которого сопоставляется, т. е. когда говорят о стандарте людям легче представить, о чем идет речь. Тема нашего урока: Стандартный вид числа. В окружающем нас мире мы сталкиваемся с очень большими и с очень маленькими числами. Где вы встречались с такими числами? Если числа очень большие или маленькие удобно ли записывать числа в таком виде? Почему? (занимает много места, времени для записи, сложно запомнить) Как вы считаете, какой выход нашли из этой ситуации. Записать с помощью степени. 598 000 000 000 000 000 Попробуйте записать это число короче. 598∙1015, 59,8∙1016, 5,98∙1017, 0,598∙1018 Все результаты верны. Подумайте, посоветуйтесь и выскажите свое мнение, какая же запись может быть стандартной. 5,98∙1017 –почему? Мы представили число в виде двух множителей. Первый множитель число принадлежащее промежутку от 1 до 10 «положительный». Второй множитель число 10 в любой степени тоже положительно, а при умножении двух положительных чисел получается только положительное число. -Итак, стандартным видом числа А называется запись вида а∙10n ,где 1≤ а<10. n- порядок числа, n-целое. Работа с учебником (с.64, п.8). Рассмотрим некоторые примеры: 25 000 = 2,5 * 104 ; 1230 = 1,23 * 103; 0,0036 = 3,6 * 10-3; 24 = 2,4 * 10; 0,5 = 5 * 10-1; 0,00038 = 3,8 * 10- 4; 560 000 000 = 5,6 * 108; 967 000 000 000 000 = 9,67 * 10 14; 0, 000 000 000 000 000 028 = 2,8 * 10 – 17. Решить устно №244. 4. Закрепление нового материала. 1) Запишите в стандартном виде. 1204 тыс.км2=1204000 км2=1,204∙106км2 2)0,0002007=2,007∙10-4 3)506 тыс.км2=506000 км2=5,06∙105км2 4)0,003008=3,008∙10-3 2) Назовите порядок числа, представленного в стандартном виде: а)1,2 * 10 9 –порядок = 9; б) 3,6 * 10 3 – порядок = 3; в) 2,7 * 10-3 – порядок = -3; г) 6,3 * 10-1 – порядок = -1; д) 4,42 * 10 5 - порядок = 5; е) 9,28 * 10- 4 – порядок = -4. 3) Запишите в стандартном виде число: а) 52 000 000 = 5,2 * 10 7; б) 2 180 000 = 2,18 * 10 6; в) 675 000 000 = 6,75 * 10 8; г) 40,44 = 4,044 * 10; д) 0,00281 = 2,81 * 10 – 3; е) 0,0000035 = 3,5 * 10- 6. 4) Запишите в стандартном виде число: а) 45 *10 3= 4,5 * 10 4; б) 117 * 10 5 = 1,17 * 10 7; в) 0,74 * 10 6= 7,4 * 10 5; г) 0,06 * 10 5 = 6 * 10 3. 5) Масса Земли равна 6 000 000 000 000 000 000 000 т, а масса атома водорода 0, 000 000 000 000 000 000 0017 г. Запишите в стандартном виде массу Земли и массу атома водорода. Решение: Масса Земли – 6 * 10 21 тонн, масса атома водорода – 1,7 9 10 – 21 граммов. 5. Физ. минутка -Разминаем руки плечи (круговые движения плечами) -Чтоб сидеть нам было легче, -Чтоб писать, считать, читать(руки пред грудью) -И совсем не уставать. -Голова устала тоже, так давайте ей поможем. -Вправо, влево, раз и два (круговые движения головой) -Думай, думай голова -Хоть зарядка коротка отдохнули мы слегка. (садимся) 6. Самостоятельная работа. Напишем графический диктант. На каждый вопрос вы даёте ответ: да + нет -. 1. Число 3∙105 записано в стандартном виде? 2. Число 0,81∙106 записано в стандартном виде? 3. Число 7,45∙10-5 записано в стандартном виде? 4. Число 50 записано в стандартном виде? 5. Верно ли высказывание: чем больше порядок, тем больше само число? 6. Если порядок числа отрицательный, то и само число отрицательно? 7. Стандартным видом числа А называется запись вида а∙10n ,где 1≤ а<10. 8. В стандартном виде можно записать любое число? 9. Различные величины и единицы измерения могут быть отрицательными? 10. Если n>0 то А>10 6. Итоги урока. Д/З. Ребята! Вот и подошёл к концу наш урок. Я прошу вас вспомнить: О чём мы сегодня вели речь на уроке? Какую запись числа называют его стандартным видом? Что такое порядок числа? Каким бывает порядок числа? Что можно сказать о числе с отрицательным порядком? С положительным? (Обучающиеся дают ответы с мест, активно участвуя в подведении итогов урока.) п 8. с. 64, решить № 245, 246, 247, 249. Придумайте задачу из различных областей знаний, где фигурируют числа записанные в стандартном виде. Выполнить на формате бумаги А4 Спасибо за урок. Урок алгебры по теме: «График обратной пропорциональности» Цели урока: научить учащихся выделять среди функций обратную пропорциональность, строить график и применять при решении упражнений; прививать аккуратность при построении графиков функций; развивать мышление и самостоятельность на уроке. Ход урока. I. Организационный момент. Эмоциональный настрой. 2. Постановка цели и мотивация. Начать наш урок хочу пословицей. Прочитайте её. Как вы понимаете смысл пословицы? МАТЕМАТИКЕ УЧИТЬСЯ – ВСЕГДА ПРИГОДИТЬСЯ. 2) Ребята, а зачем заниматься математикой? Не зря говорят: МАТЕМАТИКА – КОРОЛЕВА НАУК! БЕЗ НЕЁ НЕ ЛЕТЯТ КОРАБЛИ, БЕЗ НЕЁ НЕ ПОДЕЛИШЬ НИ АКРА ЗЕМЛИ, ДАЖЕ ХЛЕБА НЕ КУПИШЬ, РУБЛЯ НЕ СОЧТЁШЬ, ЧТО ПОЧЁМ, НЕ УЗНАЕШЬ, А УЗНАВ, НЕ ПОЙМЁШЬ! Над какой темой мы работали на предыдущем уроке? 3. Актуализация опорных знаний. Проверка д/з. Математика – это наука, которая всегда сопровождала человечество. Она призвана развивать логическое мышление, внимание, тренировать мозг. Недаром ее называют «гимнастикой ума». Так давайте выполним небольшую математическую разминку. 1. Зависимость между переменными, при которой каждому значению независимой переменной соответствует значение зависимой переменной (функция). 2. Независимая переменная или … (аргумент). 3. Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – значениями функции (график) 4. Функция, заданная формулой y=kx+b. (линейная) 5. Как называется число k в формуле y=kx+b? (угловой коэффициент) 6. Что является графиком линейной функции? (прямая) 7. Если k≠0, то график функции y=kx+b пересекает эту ось, а если k=0, то параллелен ей. Какой буквой обозначается эта ось? (икс) 8. Слово в названии функции y=kx (пропорциональность) 9. Буква латинского алфавита, которой часто обозначают функцию (игрек) 10. Один из способов задания функции (формула) Найдите область определения функций: y=x2+8; y=  ; y= ; y= ; y= 4. Изучение нового материала. Как заметил Г.Галилей, книга природы написана на математическом языке и её буквы - математические знаки и геометрические фигуры - невозможно понять её слова. И именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения, присущие природе. Впервые функция вошла в математику под именем «переменная величина» в знаменитом труде французского математика и философа Р. Декарта «Геометрия» (1637г.). С развитием науки понятие функции уточнялось и обобщалось. Основные понятия: независимая величина – аргумент, зависимая величина – функция, однозначность соответствия и др. Как известно, всякая функция описывает какие-то процессы, происходящие в окружающем нас мире. Рассмотрим, например, прямоугольник со сторонами x, y и S=8 см. Мы знаем, что x*y=8. Посмотрим, что будет происходить с другой стороной, если будем изменять одну из сторон прямоугольника, например x. Как выразить длину второй стороны? (длина второй стороны выражается формулой y=  ).Если X увеличим в 2 раза, то Y уменьшится в 2 раза; если X увеличить в 4, 5 раз, то Y уменьшится в 4, 5 раз и наоборот. Поэтому функцию y= называют обратной пропорциональностью. В общем виде функция записывается y= , где k- константа, k≠0.С такими функциями вы уже встречались на уроке физики. Закон Ома гласит, при постоянном напряжении сила тока обратно пропорциональна сопротивлению проводника и записывается I=  ; или при неизменном расстоянии скорость обратно пропорциональна времени  . Как же получить графики функций y= и y= ? (соединить плавной линией точки, построенные на координатной плоскости). Как провести график функции, если ее область определения x≠0 ? Одних точек недостаточно для построения графика функции, поэтому выясним свойства этих функций и тогда уже построим график. Что означает x≠0? (это означает, что график функции не пересекает ось OY). Может ли функция y= принимать значение 0? (нет, так как график функции не пересекает ось OX). Выясним, как изменяется Y, если X стремится к + ∞, X стремится к - ∞ и X стремится к 0, оставаясь положительным и отрицательным числом. 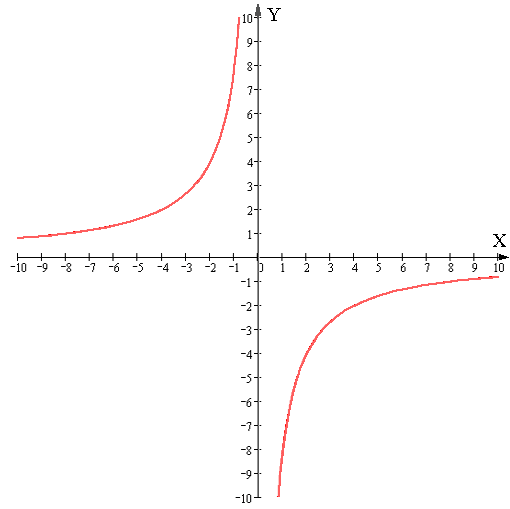 Решить устно № 312, 313, 315, 319. 5. Закрепление нового материала. Решить № 320, 322, 324. 6. Физкультминутка. Дышим носом глубоко Дышим носом глубоко- Поднимаемся легко. (Приседания.) Наклоняемся вперёд. Прогибаемся назад. Как деревья ветер гнёт. Так качаемся мы в лад- (Наклоны взад-вперёд.) Головой теперь покрутим- Так мы лучше думать будем. Поворот и поворот, А потом наоборот. (Вращения головой в стороны.) Встанем, дети, на носочки - (Потягивания — руки вверх.) На зарядке ставим точку. 7. Самостоятельная работа. Самостоятельная дифференцированная работа. 1 группа. Построить график функции y=  используя таблицу2 группа. Построить график функции y=  предварительно заполнив таблицу3 группа. Построить график функции  8. Итоги урока. Д/з. Закончи предложение: Что узнали, изучив тему… Чему научились, изучив тему… Какие испытали трудности… Выучить п. 10. решить № 321, 325 – 8 баллов, 323 -11 баллов. Творческое задание: сообщение «Из истории функции». 1 2 |