практикумы-моделирование. Уровень А. Откройте браузер на странице quickdraw withgoogle com. Попробуйте выполнить задание нарисовать несколько предметов, которые нейронная сеть попробует угадать.

• Название: Уровень А. Откройте браузер на странице quickdraw withgoogle com. Попробуйте выполнить задание нарисовать несколько предметов, которые нейронная сеть попробует угадать.
• Дата: 21.10.2022
• Размер: 181 Kb.
• Имя файла: практикумы-моделирование.doc
• Тип: Документы; #747620

И
22.10.2022
нформатика, 11 класс К.Ю. Поляков, Е.А. Еремин

6. 
   Искусственный интеллект

Уровень А.

1. 
   Откройте браузер на странице quickdraw.withgoogle.com. Попробуйте выполнить задание – нарисовать несколько предметов, которые нейронная сеть попробует угадать. Сколько из нарисованных вами изображений нейронная сеть определила правильно?
   

Ответ:

2. 
   С помощью сервиса bigjpg.com/ru выполните увеличение какого-нибудь изображения в 4 раза (можно использовать файл flowers.png). Добавьте в отчёт оригинал и полученное увеличенное изображение.
   

Оригинал	Увеличенное изображение

6. 
   Математическое моделирование

При выполнении этой работы нужно использовать шаблон – электронную таблицу в файле Кредит.xls.

Уровень A.

1. 
   Дядя Ваня решил взять кредит 100 тыс. рублей в банке на год под 13% годовых. Банк предложил ему выплачивать каждый месяц равные суммы (такой платёж называется аннуитетным). Сумма ежемесячной выплаты p вычисляется по формуле:
   

,

где S – сумма кредита, i – годовая процентная ставка кредита, делённая на 12; n – число месяцев, в течение которых нужно выплатить кредит.

Используя электронную таблицу или программу на языке программирования, определите, сколько всего денег выплатит дядя Ваня банку по процентам (сверх 100 тыс. рублей).

Ответ:

Уровень B.

2. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня выплатит по процентам не более 10000 руб.
   

Ответ:

Какова в этом случае будет величина ежемесячной выплаты:

3. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня будет ежемесячно выплачивать не более 9100 руб.
   

Ответ:

Какова в этом случае будет общая сумма выплат:

Уровень С.

4. 
   Существует ещё один вариант выплаты кредита, при котором выплачиваемая сумма изменяется (уменьшается) каждый месяц. Такая схема называется дифференцированными платежами. Выплаты за текущий месяц складываются из двух частей – выплат p₁ за основную часть кредита (100 тыс. руб) и выплат по процентам p₂.
   

Первая часть, p₁, всегда постоянна и определяется как сумму кредита, делённая на количество месяцев. Для примера, который рассмотрен в начале описания этой работы,

p₁ = 100000 : 12 = 8333,33 р.

Вторая часть, p₂, зависит от номера месяца k, поэтому будем обозначать её как p_2k. Она вычисляется как оставшаяся сумма основного долга, умноженная на годовую процентную ставку кредита, делённую на 12:



Например, в первый месяц выплат (выплат ещё не было), поэтому

p₂₁ = 100000  0,13 / 12 = 1083,33 р.

Во второй месяц оставшаяся сумма долга равна

S₁ = 100000 – 8333,33 = 91666,67 р.

При этом получается другая выплата по процентам:

p₂₂ = 91666,67  0,13 / 12 = 993,06 р.

5. 
   При ставке 13% постройте график выплат дяди Вани при дифференцированных платежах. Сколько всего денег он переплатит по процентам?
   

Ответ:

Какой способ выплат выгоднее для дяди Вани:

6. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня выплатит по процентам не более 10000 руб.
   

Ответ:

Какова в этом случае будет величина выплаты в первый месяц:

7. 
   Определите с точность до 0,1% наибольшую величину процентной ставки, при которой дядя Ваня будет ежемесячно выплачивать не более 9100 руб.
   

Ответ:

Какова в этом случае будет общая сумма выплат:

Моделирование эпидемии

Для выполнения работы откройте файл-заготовку Эпидемия.xls.

При эпидемии гриппа число больных изменяется по формуле

,

где – количество заболевших в -й день, а – количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:

,

где – общая численность жителей, – коэффициент роста и – число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):

.

Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.

Выполните моделирование развития эпидемии при и до того момента, когда количество больных станет равно нулю.

Уровень A.

1. 
   Постройте график изменения количества больных.
   

Ответ:

2. 
   Когда закончится эпидемия?
   

Ответ:

3. 
   Сколько человек переболеет, а сколько вообще не заболеет гриппом?
   

Ответ:

4. 
   Каково максимальное число больных в один день?
   

Ответ:

Уровень B.

5. 
   Изменяя коэффициент с шагом 0,1, определите, при каких значениях модель явно перестает быть адекватной.
   

Ответ:

Уровень C.

6. 
   *Сравните модель, использованную в этой работе, со следующей моделью:
   

, .

Постройте график изменений количества больных этой и предыдущей моделей на одном поле:

Анализируя результаты моделирования, докажите, что эта модель неадекватна.

Ответ:

Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?

Ответ:

Сравните поведение двух моделей при , и . Сделайте выводы.

Ответ:

6. 
   Модель «хищник-жертва»

Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.

Выполните моделирование биологической системы «щуки-караси»



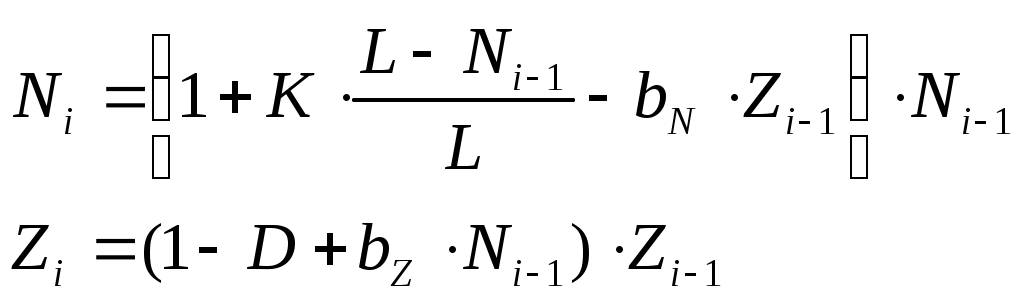
где – численность карасей

– численность щук

при следующих значениях параметров:

– коэффициент прироста карасей;

– предельная численность карасей;

– начальная численность карасей;

– начальная численность щук;

– коэффициент смертности щук без пищи;

и – коэффициенты модели.

Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.

Уровень A.

1. 
   Выполните моделирование двух популяций в течение 25 периодов. Постройте графики изменения численности карасей и щук.
   

Ответ:

2. 
   Сколько карасей и щук живут в водоеме в состоянии равновесия?
   

Ответ:

3. 
   Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
   

Ответ:

Уровень B.

4. 
   На что влияет начальная численность хищников и жертв?
   

Ответ:

5. 
   Подберите значения коэффициентов, при которых модель становится неадекватна.
   

Ответ:

bN =

bZ =

Уровень C.

6. 
   Установите значения коэффициентов и . Вставьте в отчёт график, который вы увидели:
   

Как вы можете объяснить это с точки зрения биологии?

Ответ:

7. 
   Установите значения коэффициента . Найдите экспериментально наибольшее значения коэффициента b_Z (с точностью 0,001), при котором к 25 году щуки вымирают, а численность карасей достигает предельно возможного значения.
   

Ответ:

bZ =

Как вы можете объяснить это с точки зрения биологии?

Ответ:

6. 
   Саморегуляция

Для выполнения работы откройте файл-заготовку Саморегуляция.xls.

Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:

, (*)

Эта модель отличатся от модели ограниченного роста только дополнительным множителем , где и – некоторые числа (параметры), смысл которых вам предстоит выяснить.

Уровень A.

1. 
   Выполните моделирование для 30 периодов при следующих значениях параметров модели:
   

Постройте на одном графике кривые, показывающие изменение численности по классической модели ограниченного роста и по модели (*).

Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.

Ответ:

2. 
   Постройте аналогичные графики для F = 500:
   

Сделайте вывод о том, как коэффициент F на саморегуляцию.

3. 
   Через 10 периодов в результате изменения природных условия число животных уменьшилось до 400 (то есть, ). Используйте значение F = 500. Выполните моделирование при этих условиях и постройте графики:
   

Опишите, чем отличается поведение двух сравниваемых моделей.

.

Как влияет изменение F на переходные процессы?

Уровень B.

4. 
   Повторите моделирование при и постройте графики:
   

Cделайте выводы:

Уровень C.

5. 
   Экспериментируя с моделями, найдите минимальную численность популяции , при которой она выживает в соответствии с моделью (*).
   

Ответ:

6. 
   Сделайте выводы о смысле коэффициента в модели (*).
   

Ответ:

7. 
   Сравните свойства саморегуляции для модели ограниченного роста и модели (*).
   

Ответ:

http://kpolyakov.spb.ru