Задача. Задача 1. Задача 1 (Разбор)

• Название: Задача 1 (Разбор)
• Анкор: Задача
• Дата: 31.05.2022
• Размер: 1 Mb.
• Имя файла: Задача 1.docx
• Тип: Задача; #560596

Задача 1 (Разбор) В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей? Решение: 𝑆 = 18 млн. руб. − сумма кредита 𝑟 = 10% → 𝑘 = 1 +( 𝑟/100)

𝑍 = 27 − общая сумма выплат.






Воспользуемся формулой суммы арифметической прогрессии:


-умножим числитель первой дроби на 𝑛, а числитель второй дроби приведем к общему знаменателю




__________________________________________________________________

Задача 2 (Разбор) В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы: — в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом; — с февраля по июнь нужно выплатить часть долга одним платежом. Определите, на какую сумму взяли кредит банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 156 060 рублей больше суммы взятого кредита. Решение: 𝑥 = ? − ежегодная выплата 𝑟 = 30% → 𝑘 = 1 +( 𝑟/100)

𝑍 = 156 060 руб. − общая сумма выплат

Важно отметить, что сумма трех платежей равна сумме кредита, которую и нужно найти: 𝑆 = 3 ∙ 𝑥, то есть решать систему можно по-разному, главное помнить, что необходимо найти. Также долг после последнего платежа стал равен 0, поэтому: ((𝑆 ∙ 𝑘 − 𝑥) ∙ 𝑘 − 𝑥) ∙ 𝑘 − 𝑥 = 0 − раскроем скобки

𝑆 ∙ 𝑘 3 − 𝑘 2 ∙ 𝑥 − 𝑘 ∙ 𝑥 − 𝑥 = 0 − вынесем 𝑥 за скобки

𝑆 ∙ 𝑘 3 − 𝑥 ∙ (𝑘 2 + 𝑘 + 1) = 0





____________________________________________________________________

Задача 3 (разбор) В июле планируется взять кредит на сумму 1 342 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить некоторую часть долга. Сколько рублей необходимо будет отдать, если кредит будет погашен 4 равными платежами Решение: Составим таблицу на 4 года: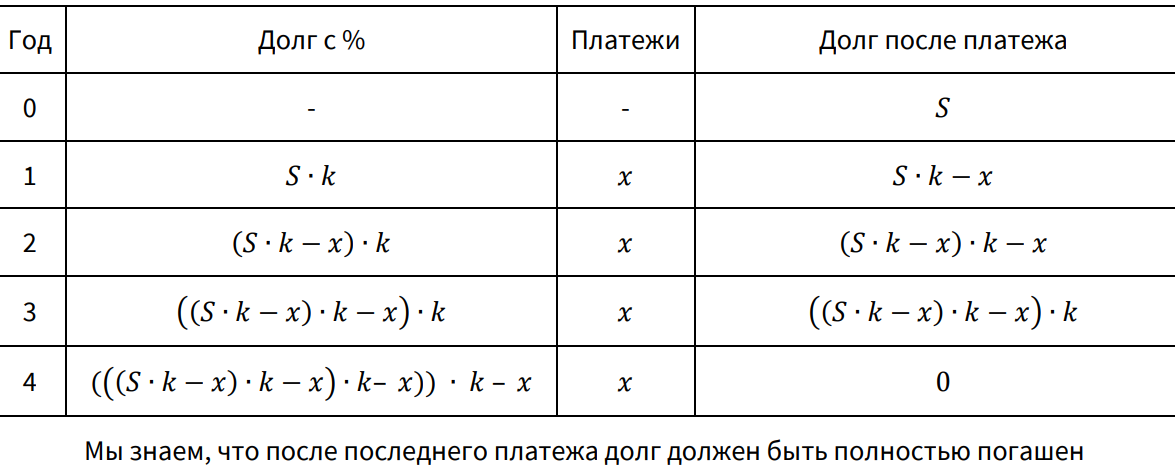




(((𝑆 ∙ 𝑘 − 𝑥) ∙ 𝑘 − 𝑥) ∙ 𝑘– х) ∙ 𝑘 – 𝑥 = 0 − раскроем скобки

((𝑆 ∙ 𝑘^2 − 𝑥 ∙ 𝑘 − 𝑥) ⋅ 𝑘 − 𝑥) ⋅ 𝑘 − 𝑥 = 0 − еще раз раскроем скобки

(𝑆 ∙ 𝑘^3 − 𝑥 ∙ 𝑘^2 − 𝑥 ∙ 𝑘 − 𝑥) ⋅ 𝑘 − 𝑥 = 0 − последний раз раскроем скобки

𝑆 ∙ 𝑘^4 – 𝑘^3 ∙ 𝑥 – 𝑘^2 ∙ 𝑥 − 𝑘 ∙ 𝑥 − 𝑥 = 0 − вынесем (−𝑥) за скобки

𝑆 ∙ 𝑘^4 − 𝑥 ∙ (𝑘^3 + 𝑘^2 + 𝑘 + 1) = 0 − выразим х




Ответ: 2 073 600

Задача 4 (разбор) В августе 2020 года взяли кредит. Условия возврата таковы - каждый год долг увеличивается на r% - с февраля по июль необходимо выплатить часть долго - кредит можно выплатить равными платежами за четыре года по 777 600 рублей или за два года равными платежами по

1 317 600 рублей Найдите r% Решение: 𝑘 = 1 + (𝑟/100)

𝑦 = 777 600 − выплата при 4 равных платежах

𝑥 = 1 317 600 − выплата при 2 равных платежах допустим мы выплатили долг за 2 года:







______________________________________________________________________Задача_5_(Разбор)'>Ответ: 20%

____________________________________________________________________

Задача 5 (Разбор) В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 47 млн рублей?

Решение: 𝑆 = 20 млн. − сумма кредита 𝑟 = 30% → 𝑘 = 1 + (𝑟/100)

𝑍 = 47 − общая сумма выплат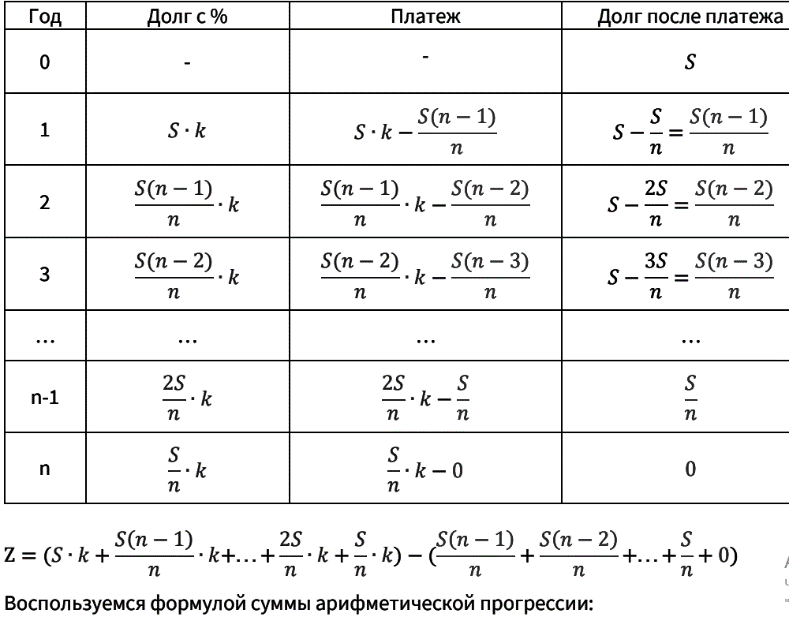









____________________________________________________________________

Задача 6 (Разбор) 31 декабря 2017 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплат кредита следующая:

— 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга,

— затем Тимофей переводит в банк платеж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он отдал банку, если бы смог выплатить долг за 2 равных платежа?

Р ешение: Составим таблицу на 3 года

𝑥 = 1925000 ⋅ 1,728 𝑥 = 3326400 𝑥 = 3326400, но мы нашли сумму одного платежа, всего их 3 То есть всего придется отдать 3326400 ⋅ 3 = 9979200




Мы знаем, что после последнего платежа долг должен быть полностью погашен: (𝑆 ∙ 𝑘 − 𝑥) ∙ 𝑘 − 𝑥 = 0 − раскроем скобки 𝑆 ∙ 𝑘 2 − 𝑘 ∙ 𝑥 − 𝑥 = 0 − вынесем (−𝑥) за скобки 𝑆 ∙ 𝑘 2 − 𝑥 ∙ (𝑘 + 1) = 0 − выразим 𝑥 𝑥 = 𝑆𝑘 2 𝑘+1 Подставим данные значения 𝑥 = (7007000⋅1,44)/ (2,2) Сократим числитель и знаменатель на 2,2 значит 𝑥 = 3185000 ⋅ 1,44 𝑥 = 4586400 - мы нашли сумму одного платежа, всего их 2. То есть всего придется отдать 4586400 ⋅ 2 = 9172800 Находим разницу между суммами платежей за 3 и за 2 года 9979200 − 9172800 = 806400

Ответ: 806400

Задача 7 (разбор) Взяли кредит в банке на сумму 250 000 рублей под r % процентов годовых и выплатили за 2 года платежами 150 000 рублей в первый год и 180 000 рублей — во второй.

Найдите r. Решение: 𝑘 = 1 + 𝑟 100 𝑥1 = 150 000 𝑥2 = 180 000 𝑆 = 250 000

Мы выплатили долг за 2 года:



(𝑆 ∙ 𝑘 − 𝑥1 ) ∙ 𝑘 − 𝑥2 = 0 − раскроем скобки

𝑆 ∙ 𝑘^2 − 𝑘 ∙ 𝑥1 − 𝑥2 = 0 подставим данные значения

250 000𝑘^2 − 150 000𝑘 − 180 000 = 0 − сократим на 10 000

25𝑘^2 − 15𝑘 − 18 = 0 Решим квадратное уравнение:

𝐷 = 225 − 4 ⋅ 25(−18) = 2025

𝑘1 = (15+4)/ (50) = 1,2

𝑘2 = (15−45)/ (50) = −0,6 но процент не может быть отрицательным

Таким образом 𝑘 = 1,2 Значит 𝑟 = 20% Ответ: 𝟐𝟎%

____________________________________________________________________

Задача 8 (Разбор) 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r. Решение: 𝑆 − сумма кредита 𝑘 = 1 + 𝑟 100 𝑍 = 1,3𝑆 − общая сумма выплат

𝑛 = 19 − число месяцев




Воспользуемся формулой суммы арифметической прогрессии:





Задача 9 (Разбор) 15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы: − 1-го числа k-ого месяца долго возрастёт на 1% по сравнению с концом предыдущего месяца; − со 2-го по 14-е число k-того месяца необходимо выплатить часть долга; − 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?

Решение:

𝑆 − сумма кредита 𝑘 = 1 + (𝑟/100) = 1,01

𝑍 = 1,2𝑆 − общая сумма выплат

𝑛 − число месяцев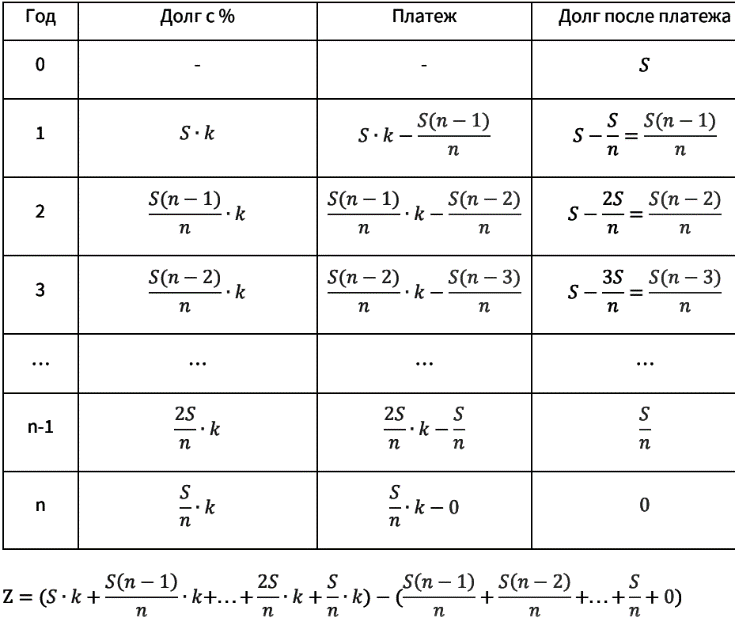





Воспользуемся формулой суммы арифметической прогрессии: