Формулы. Усечённый конус Если в усеч конус можно впис окр., то
 Скачать 76.63 Kb. Скачать 76.63 Kb.
|
|
Тела вращения. Цилиндр 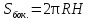 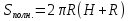 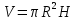 Конус 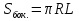 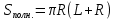 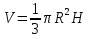 Усечённый конус 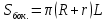 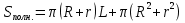 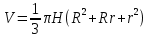 Если в усеч. конус можно впис. окр., то 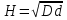 Сфера 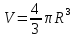 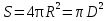 Пирамида: V= 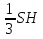 Комбинации сферы с другими телами (радиус): 1. Описанной около правильного тетраэдра с ребром a: 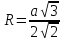 2. Описанной около правильной треугольной пирамиды с высотой h и ребром основания a: 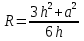 3. Описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a: 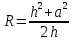 4. Описанной около конуса: 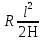 5. Описанной около призмы: 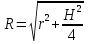 Вектора. 1. Расстояние между точками 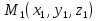 и и 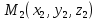 : : 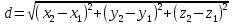 2. Уравнение плоскости по 3-м точкам 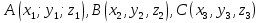 : : 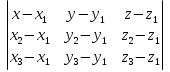 3. Определитель второго порядка: 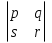 =ps-rq =ps-rq4. 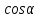 между прямой, заданной вектором между прямой, заданной вектором 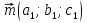 и плоскостью, заданной уравнением и плоскостью, заданной уравнением 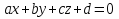 : : 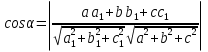 5. Длина вектора по его координатам 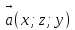 : : 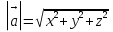 6. Расстояние от точки 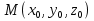 и плоскостью, заданной уравнением и плоскостью, заданной уравнением 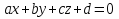 : : 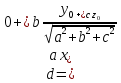 7. Произведение векторов 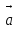 и и 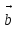 : : 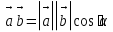 = = 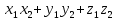 8. Угол между двумя прямыми, заданными направляющими векторами: 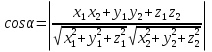 Окружность. 1. Длина дуги окр. L радиуса R с центральным углом  (в радианах): L=R (в радианах): L=R 2. Площадь сектора радиуса R с центральным углом 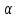 : : 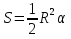 3. Длина окружности: 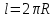 4. Площадь круга: 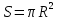 Треугольник. 1. Высота равнобедренного треугольника: 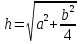 2. Высота, медиана и биссектриса равнобедренного тр.: 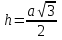 3. Длина биссектрисы: 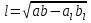 , , 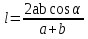 4. Высота, проведённая из прямого угла: 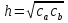 5. Длина медианы: 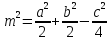 6. Окр., вписанная в прям. тр.: 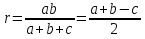 7. S прям. тр.: 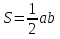 ; через впис. окр.: S=de ; через впис. окр.: S=de8. S равнобедр. тр.: 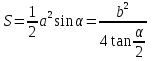 9. S равносторон. тр.: 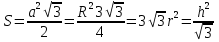 10. S через стороны: 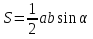 11. 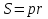 , p-полупериметр, r-впис. окр. , p-полупериметр, r-впис. окр.12. 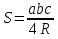 , R-опис. окр. , R-опис. окр.13. Герона: 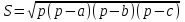 , p-полупериметр , p-полупериметр14. Биссектриса: А) Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам: 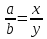 Б) Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. 15. Высота: А) В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному. Б) В остроугольном треугольнике две его высоты отсекают от него подобные треугольники. 16. Медиана: А) Медиана разбивает треугольник на два треугольника одинаковой площади. Б) Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. В) Весь треугольник разделяется своими медианами на шесть равновеликих треугольников. 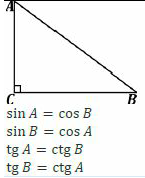 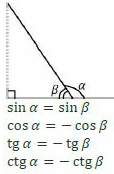 17. Серединный перпендикуляр: А) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. Б) Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника. 18. Теорема Менелая: 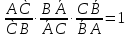 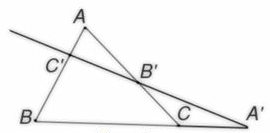 |
