энгс. Условия притока жидкости и газов к скважинам 1 Приток жидкости к скважине
 Скачать 2.74 Mb.
|
|
ГЛАВА 1 УСЛОВИЯ ПРИТОКА ЖИДКОСТИ И ГАЗОВ К СКВАЖИНАМ 1.1 Приток жидкости к скважине При эксплуатации скважины движение пластовой жидкости осуществляется в трех системах пласт-скважина-коллектор, которые действуют независимо друг от друга, при этом взаимосвязаны между собой.  Рис. 1.1. Схема добычи нефти из пласта. Приток жидкости в скважины происходит под действием разницы между пластовым давлением и давлением на забое скважины. Разность между пластовым и забойным давлением называется депрессией на пласт.  Р = Рпл - Рзаб (1.1)Так как движение жидкости в пласте происходит с весьма малыми скоростями, то оно подчиняется линейному закону фильтрации - закону Дарси. При постоянной толщине пласта и открытом забое скважины жидкость движется к забою по радиально-сходящимся направлениям. В таком случае говорят о плоскорадиальной форме потока. Если скважина достаточно продолжительно работает при постоянном забойном давлении, то скорость фильтрации и давление во всех точках пласта перестают изменяться во времени и поток является установившимся. Рассмотрим задачу притока жидкости в скважину в круговом пласте, схема которого представлена на рис. 1.2. 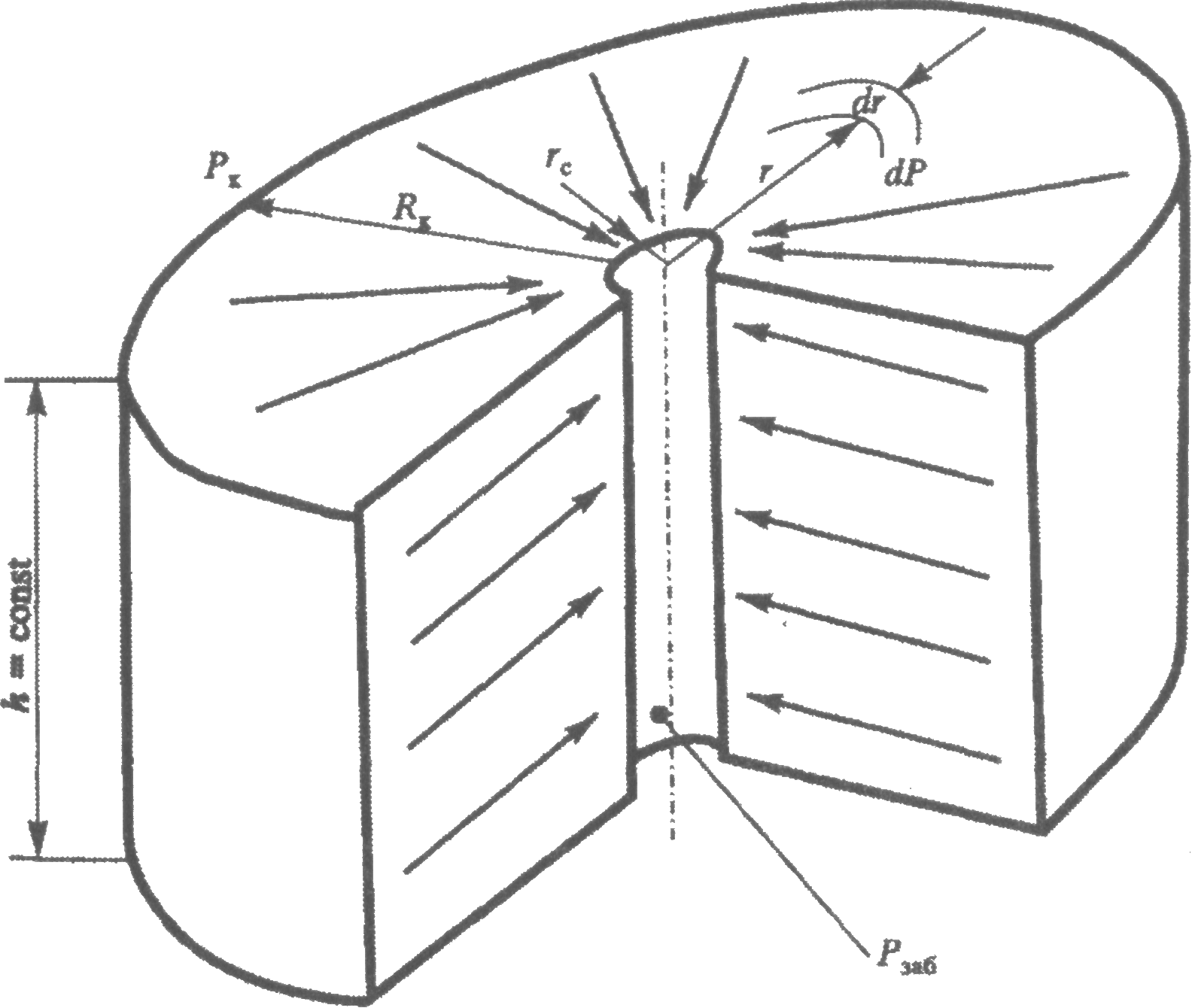 Рис. 1.2. К выводу уравнения Дюпюи Для решения задачи введем следующие допущения: 1. Пласт круговой, в центре которого расположена единственная совершенная скважина. 2. Пласт однородный и изотропный постоянной толщины. 3. Процесс течения флюида изотермический  = const).4. Движение жидкости плоскорадиальное и соответствует закону Дарси. 5. В процессе фильтрации отсутствуют любые физические и химические реакции. Запишем уравнение Дарси:  (1.2)где Q — объемный расход жидкости, м3/с; F— поверхность фильтрации, м2;  — перепад давлений, Па; — вязкость флюида, Па с;l — путь течения флюида, м; к — коэффициент пропорциональности, который учитывает не только среду в которой осуществляется фильтрация, но и все процессы взаимодействия между фильтрующимся флюидом и твердой поверхностью среды, м2. Для схемы рис. 1.2 обозначим: Rk — радиус контура питания (равен половине расстояния между двумя соседними скважинами), м; rс— радиус скважины, м; h— толщина пласта, м; Рк— давление на контуре питания, Па; Рзаб — давление на забое скважины, Па. Выделим мысленно (рис. 1.2) на расстоянии г от оси скважины элемент пласта толщиной dr. Перепад давлений на этом элементе обозначим через dP. Поверхность фильтрации для выделенного элемента такова:  Запишем уравнение Дарси для рассматриваемой схемы: 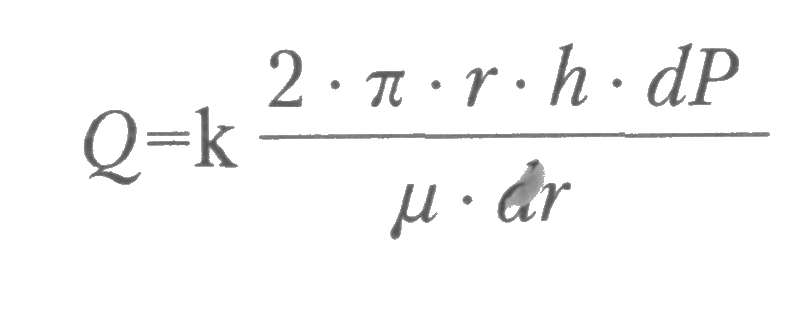 После разделения переменных получим: 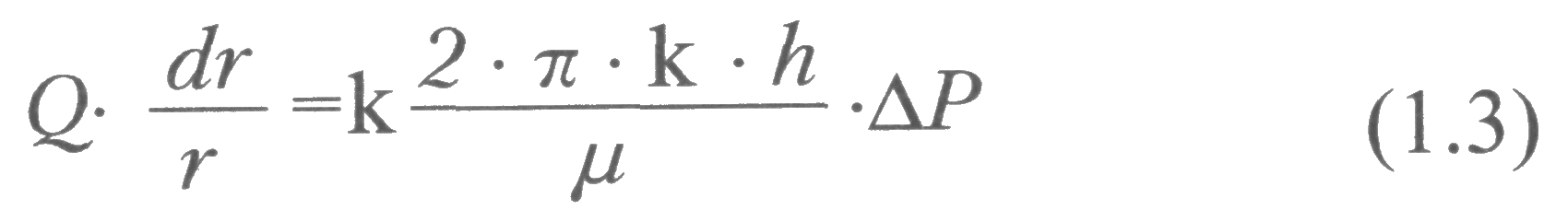 Пределами интегрирования для уравнения (1.3) являются: по P:от Рk до Рзаб; по r. от Rкдо гс. Таким образом, имеем: 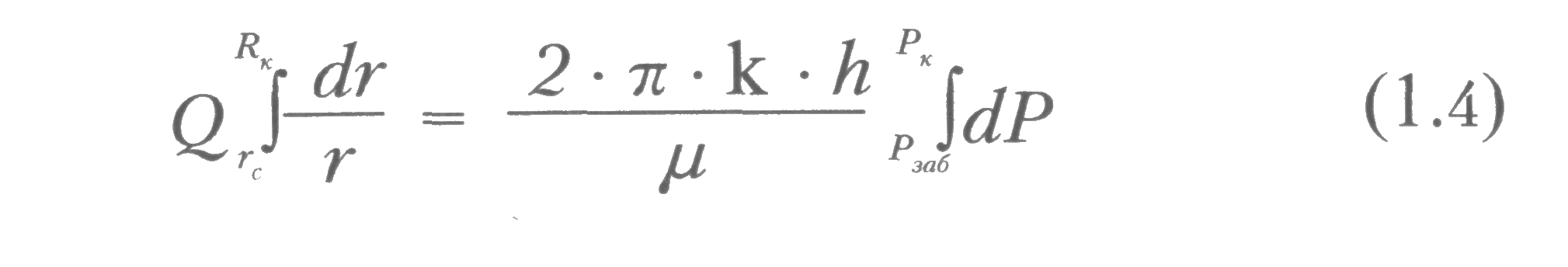 После интегрирования получаем: 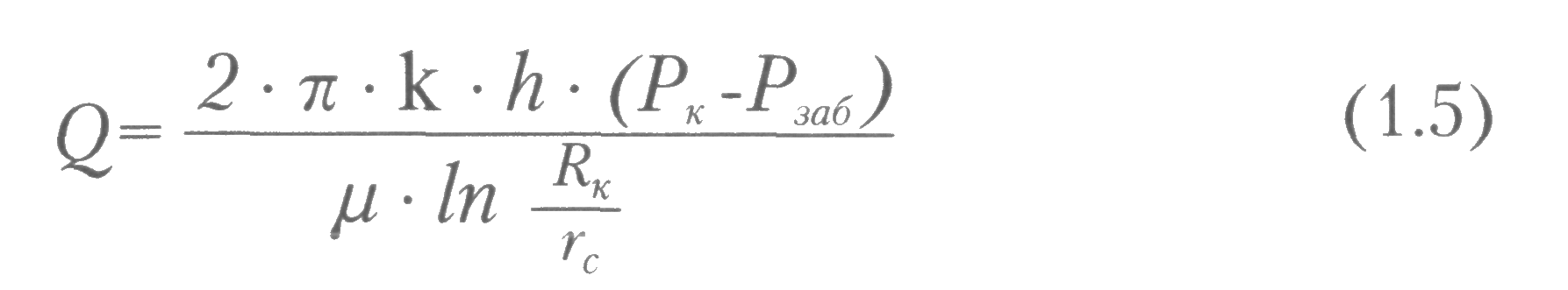 Уравнение (1.5) называется уравнением Дюпюи и описывает приток жидкости в скважину для схемы на рис. 1.3 при принятых допущениях. Как видно из (1.5), распределение давления в пласте вокруг работающей скважины является логарифмическим, что представлено на рис. 1.3. 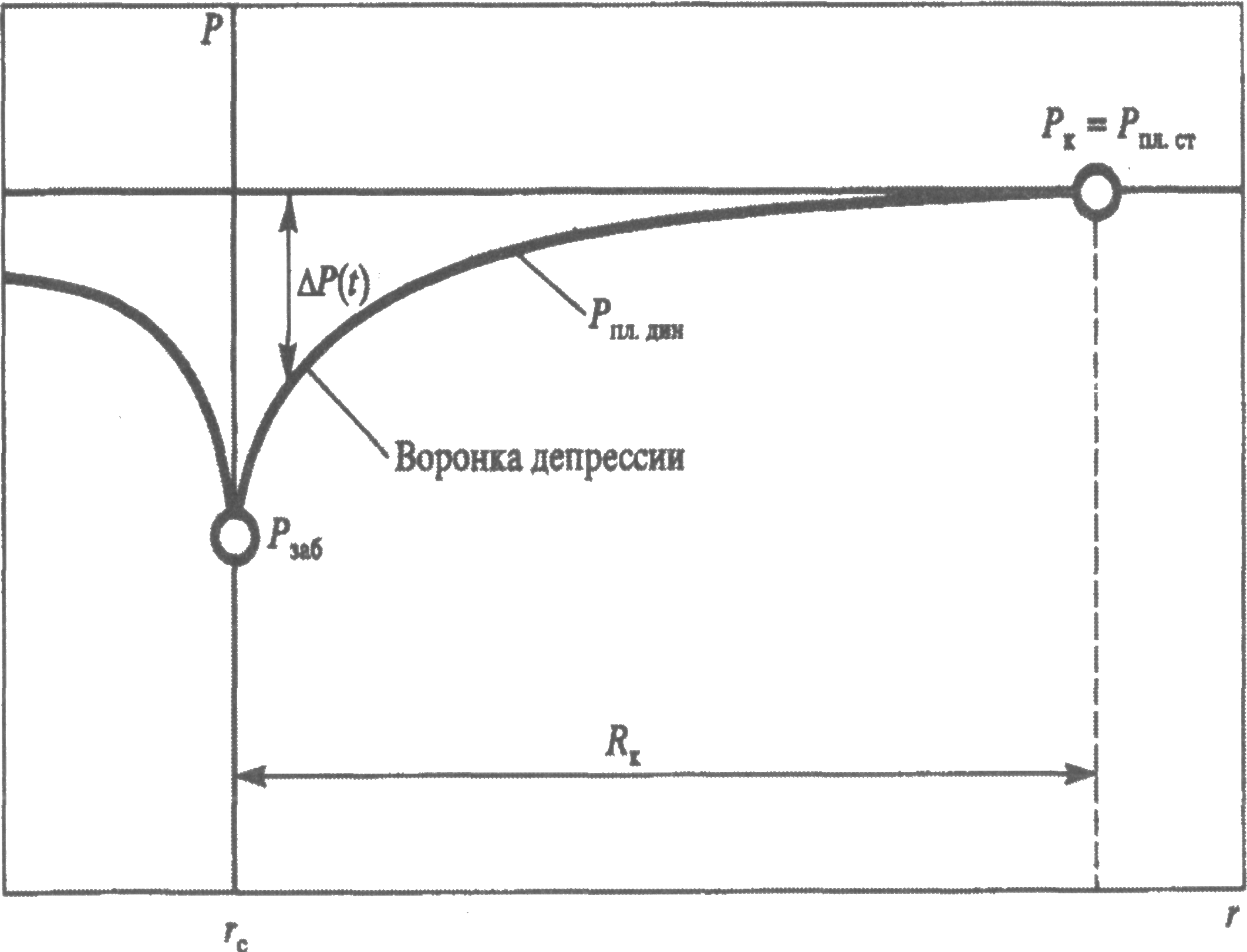 Рис. 1.3. Распределение давления в пласте вокруг работающей скважины Давление на контуре питания Ркявляется пластовым статическим давлением Pплст, в дальнейшем просто Рпл (Рплст — статическое пластовое давление — давление, которое существует в системе до момента отбора продукции, т.е. когда Q = 0). Давление вокруг работающей скважины в любой точке пласта (между давлением на забое скважины и давлением на контуре питания) называется динамическим пластовым давлением Рплдин. Динамическое пластовое давление на стенке скважины будем называть забойным давлением Рза6. 1.2. Виды гидродинамического несовершенства скважин Процесс течения продукции в пористой среде сопровождается определенными фильтрационными сопротивлениями. В призабойной зоне скважины возникают дополнительные фильтрационные сопротивления, связанные, во-первых, с наличием самой скважины и, во-вторых, с конкретным ее исполнением. Для сравнения скважин между собой и оценки каждой конкретной скважины вводятся понятия гидродинамически совершенной скважины и гидродинамически несовершенных скважин. На рис. 1.4 приведены схемы гидродинамически совершенной и гидродинамически несовершенных скважин. Рис. 1.4. Схемы гидродинамически совершенной (а) и гидродинамически несовершенных скважин: б - по степени вскрытия; в - по характеру вскрытия; г - по степени и характеру вскрытия: 1 - обсадная колонна; 2 - цементный камень; 3 - перфорационное отверстие; 4-перфорационный канал 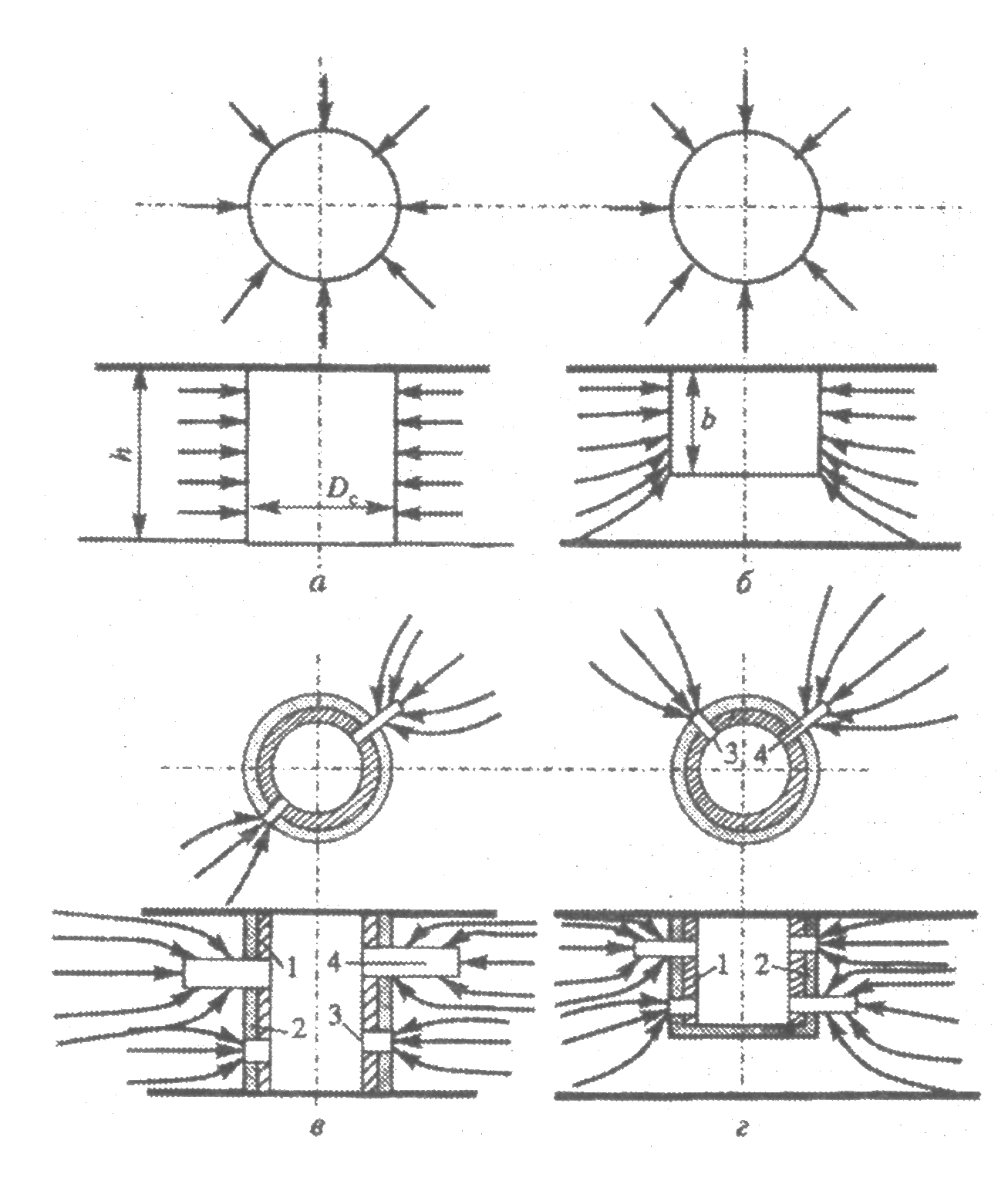 Под гидродинамически совершенной будем понимать такую скважину, которая вскрыла продуктивный горизонт на всю его толщину h и в которой отсутствуют любые элементы крепи (обсадная колонна, цементный камень, забойные устройства), т.е. скважина с открытым забоем. При течении продукции в такую скважину фильтрационные сопротивления обусловлены только характеристикой продуктивного горизонта и являются минимально возможными (рис. 1.4 а). Большинство реальных скважин относятся к гидродинамически несовершенным. Среди гидродинамически несовершенных скважин выделяют:1. Несовершенные по степени вскрытия (рис. 1.4 б). Несовершенными по степени вскрытия называются скважины, которые вскрывают продуктивный горизонт не на всю толщину. 2. Несовершенные по характеру вскрытия (рис. 1.4 в). Несовершенными по характеру вскрытия называются скважины, которые вскрывают пласт на всю толщину, но скважина обсажена и проперфорирована. 3. Несовершенные по степени и характеру вскрытия (рис. 1.4 г). Несовершенными по степени и характеру вскрытия называются скважины, которые вскрывают продуктивный горизонт не на всю толщину и скважина обсажена и проперфорирована. При расчете дебита скважин их гидродинамическое несовершенство учитывается введением в формулу Дюпюи коэффициента дополнительных фильтрационных сопротивлений С: 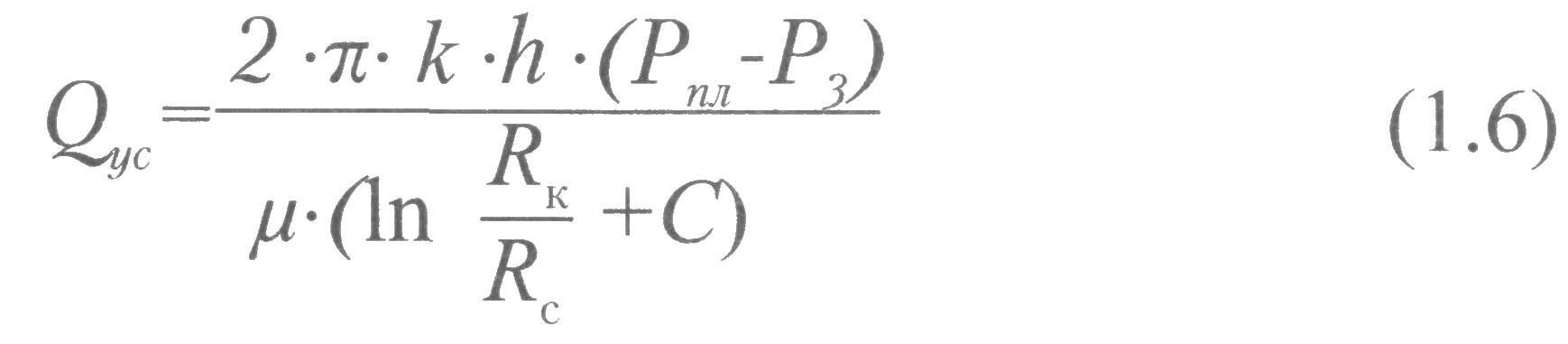 Величина коэффициента дополнительных фильтрационных сопротивлений зависит от степени вскрытия пласта, плотности перфорации, длины и диаметра перфорационных каналов. Коэффициент дополнительных фильтрационных сопротивлений можно представить в виде: С = С1+ С2(1.7) где С1- коэффициент, учитывающий несовершенство скважины по степени вскрытия. Этот коэффициент учитывает возрастание фильтрационных сопротивлений за счет изменения геометрии течения жидкости. Он будет зависеть от толщины продуктивного пласта h, диаметра скважины по долоту Dc и от относительного вскрытия пласта 8. Коэффициент С1определяется по специальным графикам.  где b- часть толщины продуктивного горизонта, вскрытого скважиной. С2- коэффициент, учитывающий несовершенство скважины по характеру вскрытия. Дополнительные фильтрационные сопротивления для таких скважин связаны с изменением геометрии течения продукции вследствие наличия перфорационных отверстий и каналов. Он будет зависеть от плотности перфорации (количества отверстий) на один погонный метр п; средней длины перфорационного канала l; диаметра перфорационного канала d. Коэффициент С2также определяется по специальным графикам. 1.3. Коэффициент гидродинамического совершенства скважины Любое гидродинамическое несовершенство скважины приводит к снижению дебита. В общем случае дебит несовершенной скважины Qhcзаписывается в виде: 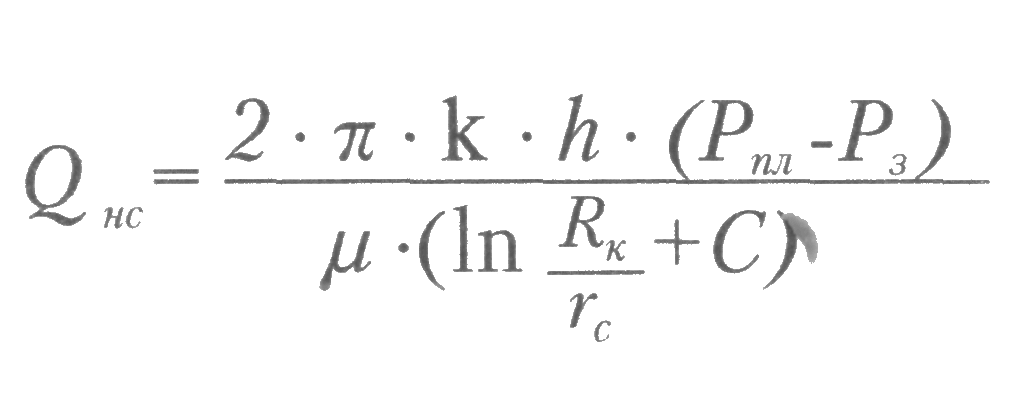 Коэффициентом гидродинамического совершенства скважины ф называется отношение дебита несовершенной скважины Qhcк дебиту совершенной скважины Qc, вычисляемому по формуле (1.5).  Учет гидродинамического несовершенства скважины может быть выполнен с использованием понятия приведенного радиуса скважины rпр. Приведенный радиус скважины - это радиус такой фиктивной совершенной скважины Qфс , дебит которой равен дебиту реальной несовершенной скважины Qрс. Для совершенной скважины rпр=rс, для несовершенных rпр <rс. Формулу (1.6) можно представить с использованием понятия приведенного радиуса скважины rспр: 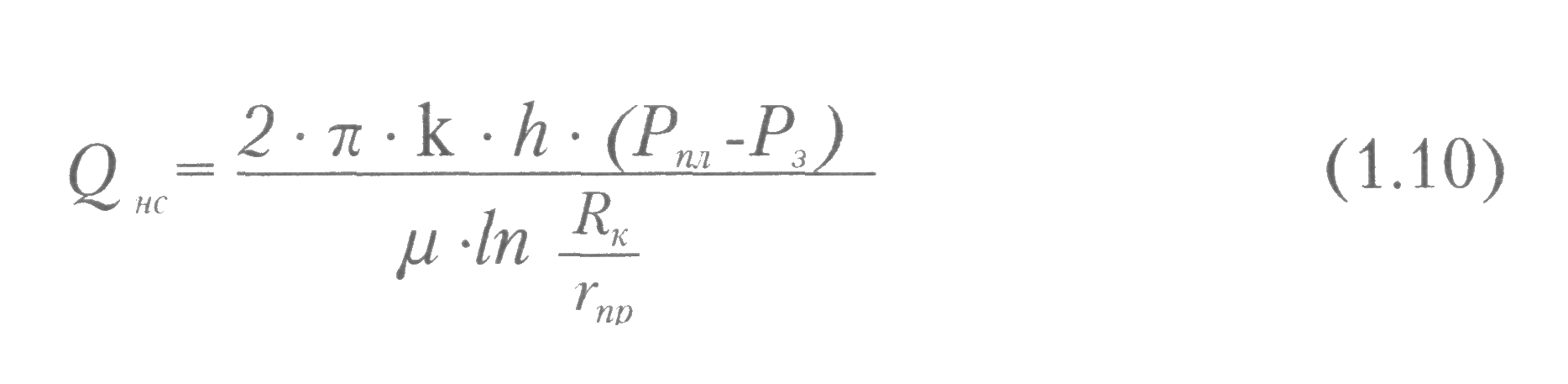 Численная величина приведенного радиуса скважины может быть определена по результатам исследования скважины на нестационарном режиме. В настоящее время гидродинамическое совершенство скважин рассчитывается по результатам экспериментального определения приведенного радиуса rпр, что существенно повышает точность, так как отпадает необходимость определения С1и С2по специальным графикам при заведомо недостоверной информации. 1.4. Оптимальный и потенциальный дебиты скважин Один из важнейших вопросов в добыче нефти и газа - установление обоснованной величины отбора нефти (газа) как из отдельных скважин, так и из залежи в целом. При прочих равных условиях максимальный дебит скважины можно получить при максимальной депрессии на пласт. Очевидно, что максимальная депрессия будет при Рзаб=0. Дебит скважины, получаемый при максимальной депрессии, называется потенциальным дебитом. Однако далеко не во всех скважинах можно добывать нефть (газ) при потенциальном дебите. Чаще всего задолго до наступления максимальной депрессии эксплуатационная обсадная колонна может быть смята внешним давлением. Возможно также интенсивное разрушение горной породы, слагающей пласт, при увеличении на него депрессии. Кроме того, при максимальной депрессии нерационально расходуется пластовая энергия вследствие бурного выделения из нефти растворенного газа и проскальзывания его в скважину без дополнительных работ по вытеснению нефти. По указанным и некоторым другим причинам приходится ограничивать отбор жидкости (газа) из пласта, чтобы получить из пласта наибольшую нефтеотдачу, а сам процесс добычи протекал бесперебойно, скважины не выходили из строя вследствие чрезмерного отбора флюидов. Следовательно, для каждой скважины в зависимости от условий эксплуатации, которые могут изменяться, существует какой-то оптимальный отбор жидкости. Величина оптимального отбора и является максимальным дебитом для скважины, при котором учитываются геолого-технические и экономические требования. Дебит скважины, удовлетворяющий указанным требованиям, называют оптимальным дебитом. Оптимальный дебит служит технической нормой добычи нефти (газа) из скважины. Контрольные вопросы: 1. Условия притока жидкости в скважину. 2. Какие допущения вводятся для вывода формулы Дюпюи. 3. Какие величины входят в формулу Дюпюи? 4. Охарактеризуйте виды гидродинамического несовершенства скважин. 5. Дайте характеристику гидродинамически совершенной скважине. 6. Чем учитывается несовершенство скважины? 7. Как определяется коэффициент совершенства скважины? 8. Дайте понятия оптимального и потенциального дебитов. |