Устойчивость систем. Устойчивость систем автоматического управления
 Скачать 154.25 Kb. Скачать 154.25 Kb.
|
|
УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ Понятие устойчивости системы управления связано со способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели её из этого состояния. Система называется устойчивой, если из возмущенного состояния А2 она перейдет в некоторую конечную область, окружающую невозмущенное состояние равновесия А0 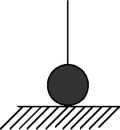 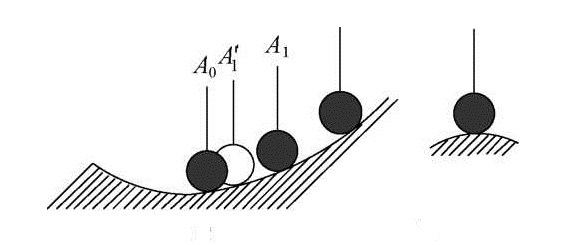 А2 А0 Ао а) б) в) Иллюстрации устойчивости положений равновесия системы: а -устойчивое; 6 - неустойчивое; в - безразличное Решение дифференциального уравнения системы автоматического управления относительно регулируемой величины имеет вид суммы функции x(t)перех, описывающей переходный процесс и функции x(t)уст, описывающей установившийся режим. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то реальная система будет устойчивой (Рис.1) Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то реальная система будет неустойчивой (рис.2) 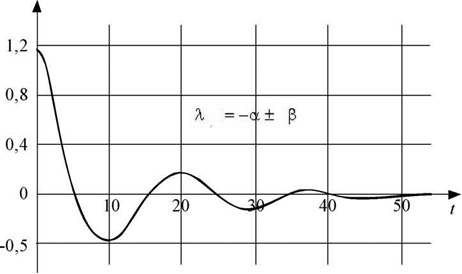 Рис. 1 Устойчивая система 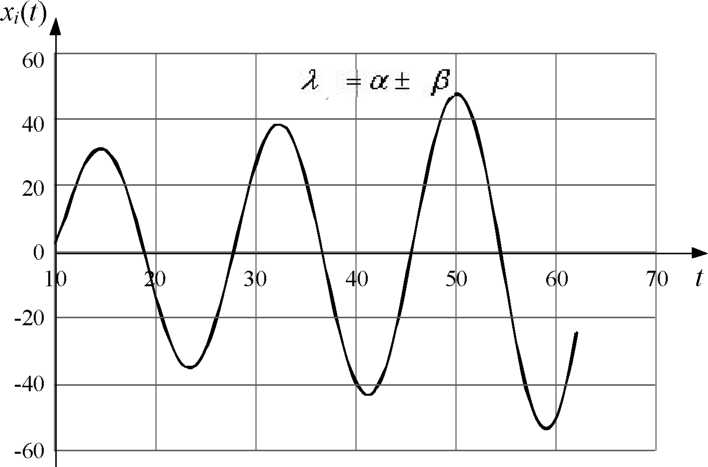 Рис.2 Неустойчивая система Переходную составляющую системы второго порядка можно представить в виде: 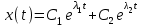  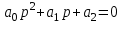 имеют отрицательные вещественные части ЗАДАНИЕ Найти корни характеристического уравнения системы второго порядка и определить, является ли система устойчивой. Сделать вывод, какой вариант системы является устойчивым. Коэффициенты характеристического уравнения берутся из таблицы по номеру варианта
Сделать рисунки полиномов характеристического уравнения (рис.3) и зависимостей переходного процесса от времени (рис.1 и 2) и сделать выводы о характере переходного процесса (апериодический при вещественных корнях или колебательный при комплексных корнях) 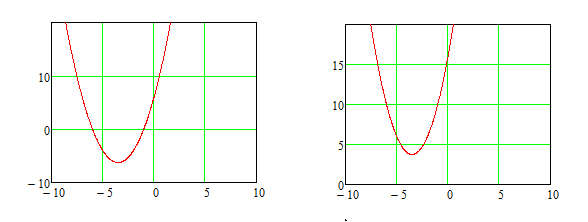 а) корни вещественные, б) корни комплексные Рис.3 Полиномы характеристического уравнения |
