практическая. Математика практическая. Узулен Мария Сергеевна
 Скачать 54.09 Kb. Скачать 54.09 Kb.
|
Практическое задание
дисциплине
Пермь 2021 Задание 1 Решить систему линейных алгебраических уравнений 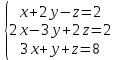 Решение: Решим систему трех уравнений методом Крамера. Находим определитель системы по правилу треугольника. 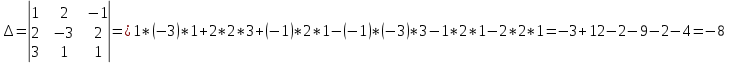 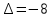 Находим определитель 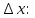 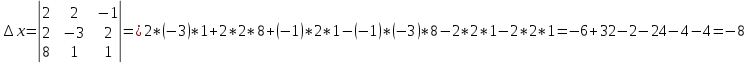 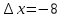 Находим определитель 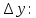 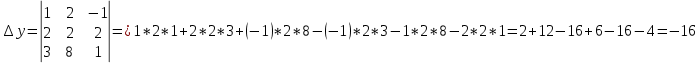 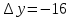 Находим определитель 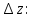 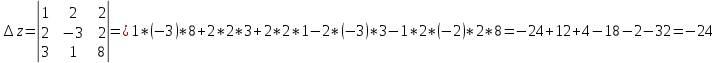 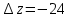 Находим неизвестные по формулам Крамера: x= 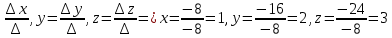 Проводим проверку: 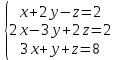 1+2*2-3=1+4-3=2, 2 = 2, верно. 2*1-3*2+2*3=2-6+6=2, 2 =2, верно. 3*1+2+3=3+2+3=8, 8 = 8, верно. Ответ: (1;2;3) Задание 2 Дано z1 = 5 – 4i и z2 = –1 – i. Выполнить действия: А) z1+ z2; Б) z1 × z2; В) z1 / z2. Решение: А) z1+ z2 = 5 – 4i + (–1) – i Суммой комплексных чисел z1=а1+b1i и z2=a2+b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть – сумме мнимых частей чисел z1 и z2, то есть z = (a1+a2)+(b1+b2)i. Следовательно, a1= 5, b1= -4, a2 = -1, b2 = -1. Подставляем значения: (5+(-1)) + (-4+(-1))i = 4-5i Б) z1 × z2 = (5 – 4i) * (–1 – i) = -5 – 5i + 4i – 4 Произведением комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число z, определяемое равенством: z = (a1a2 - b1b2) + (a1b2+ a2 - b1)i. Подставляем значения: (5*(-1)-(-4)*(-1))+(5*(-1)+(-1)*(-4))i = (-5-4) + (-5+4)i = -9 – i В)z1 / z2 = (5 – 4i) / (–1 – i) 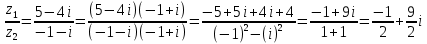 = -0,5 + 4,5i = -0,5 + 4,5iОтвет: А) 4 – 5i Б) -9 – i В) -0,5 + 4,5i Задание 3 Найти математическое ожидание и дисперсию, заданной законом распределения:
Решение: Найдем математическое ожидание случайной величины х по данной формуле: 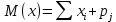 М (х) = (-5)*0,4+2*0,3+3*0,1+4*0,2= -0,3 Найдем закон распределения для случайной величины х2:
Найдем математическое ожидание от х2 по данной формуле: 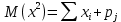 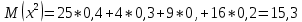 Найдем дисперсию ожидание случайной величины х по формуле: 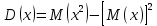 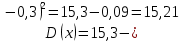 Ответ: 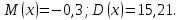 Задание 4 Вычислить предел 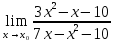 при x0=2. при x0=2.Решение: Подставим x0=2 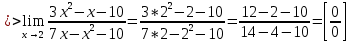 . .В данном случае мы получили неопределенность типа 0/0. Необходимо преобразовать числитель и знаменатель выражения. Данные выражения представляют собой квадратные многочлены, поэтому, пользуюсь формулой 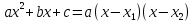 разложения квадратного многочлена на множители, разложим на множители числитель и знаменатель. разложения квадратного многочлена на множители, разложим на множители числитель и знаменатель.Найдем корни первого многочлена: 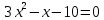 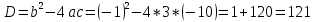 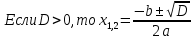 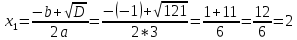 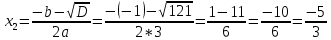 Найдем корни второго многочлена: 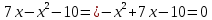 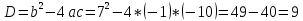 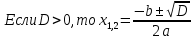 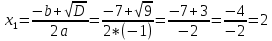 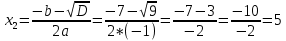 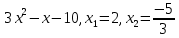 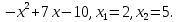 Подставляем значения: 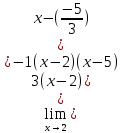 Ответ: 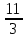 Задание 5 Найти производную функции 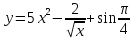 . .Решение: 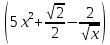 `= `=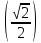 `+ `+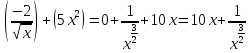 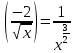 Производную этого выражения находим по формуле: 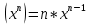 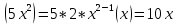 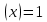 При вычислении были использованы следующие правила дифференцирования: 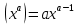 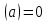 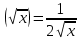 Ответ: 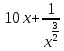 Задание 6 Вычислить неопределенный интеграл 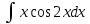 . .Решение: Определим u и dv: u = x dv = cos(2x)dx Вычислим (2x)dx дифференциал по формуле: du = u`dx du = dx dv = cos(2x)dx Определим v путем вычисления интеграла: 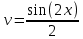 Подставим u = x, 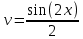 du = dx и dv = cos(2x)dx в 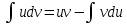 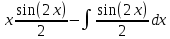 Используем св-во интегралов: 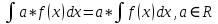 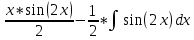 Преобразуем интеграл, используя подстановку: t = 2x 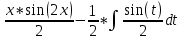 Используем св-во интегралов: 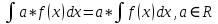 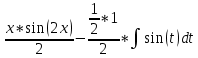 Умножим дроби: 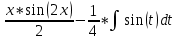 Используя 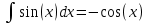 , найдем интеграл: , найдем интеграл: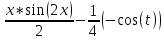 Сделаем обратную замену: t = 2x 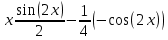 Упростим выражение: 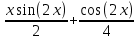 Ответ:  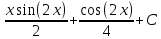 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
