Вайсберг_Астрономия для астрологов-1. В. А. Астрономия для астрологов в 3х частях. М. Цаи, 1992. 87 с. Isbn 5866610078 Эта книга
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
|
z ИЕеЕсИЫй Для астрономов представляет интерес еще один большой круг небесной сферы, образованный пересечением небесной сферы с плоскостью галактического экватора, т.е. плоскостью симметрии Млечного Пути (рис. II.7). Прямая, перпендикулярная плоскости галактического экватора и проходящая через центр небесной сферы, пересекает ее в двух диаметрально противоположных точках — северном Г и южном Г" полюсах галактики. Рис.И.7.Галактический экватор Все перечисленные элементы небесной сферы, кроме небесного экватора, неподвижны относительно наблюдателя и не участвуют в суточном вращении небесной сферы, а небесный экватор вращается вместе с небесной сферой, скользя в неподвижных точках востока и запада. Все остальные небесные светила и точки небесной сферы участвуют в ее суточном вращении, перемещаясь по малым кругам, плоскости которых параллельны плоскости небесного экватора. ІІ.З. Системы небесных координат Принцип построения любой системы небесных координат достаточно прост. Для определения координатной сетки выбирают один из больших кругов небесной сферы — истинный горизонт, небесный экватор, эклиптику или галактический экватор — и принимают его за базовый для данной координатной системы. "Горизонтальную" составляющую сетки координат представляют выбранный базовым большой круг небесной сферы и ее малые круги, параллельные большому. "Вертикальную" составляющую координатной сетки представляют большие круги, перпендикулярные выбранному базовому. Наиболее древней и наиболее часто используемой астрологами является эклиптическая система координат. Эта система — основа всех старинных атласов звездного неба. Координаты звезд в эклиптической системе не меняются в течение суток и не зависят от места нахождения наблюдателя. В горизонтальной системе координат координаты небесных тел зависят от места наблюдения на Земле. Из-за этого горизонтальная система не подходит для построения звездных карт, но очень удобна для вычисления положения небесных тел относительно горизонта. Иногда в горизонтальной системе небесных координат измеряют и координаты места на Земле. Эта система удобна для определения видимости небесных тел и весьма полезна в астрологии. В экваториальной системе небесных координат сетка координат вращается вместе с небесной сферой, и экваториальные координаты звезд остаются практически неизменными на протяжении больших промежутков времени. Эта система не зависит от времени суток и места наблюдения на Земле и удобна для использования в звездных каталогах и на звездных картах. Существует и еще одна система экваториальных небесных координат, где одна из координат — часовой угол — зависит не только от времени наблюдения, но и от места на земной поверхности. Она удобна для измерения времени. В последнее время для изучения нашей галактики используется галактическая система небесных координат. Экваториальные координаты небесных тел астрономы определяют непосредственно из наблюдений, а эклиптические и галактические получают путем вычислений из экваториальных. Системы небесных координат подразделяют также в зависимости от положения их центра в пространстве: mono-центрическая — та, в которой центр находится на поверхности Земли; геоцентрическая система небесных координат — если центр координат в центре Земли. Другие планетоцентрические системы координат, например, селеноцентрическая для Луны, афоцентрическая для Венеры, арео-центрическая для Марса — интереса для астрологов не представляют, чего нельзя сказать о гелиоцентрической системе. Н.3.1. Горизонтальная система Горизонтальную систему используют тогда, когда необходимо знать условия видимости того или иного небесного тела в определенный момент времени. Горизонтальная система координат (рис. II.8) строится на истинном (математическом) горизонте (см. рис. II. 1). Ее координатную сетку составляют малые круги, параллельные плоскости истинного горизонта и называемые кругами равной высоты, или альмукантарами (от арабского "к у а н т а р а" — изгибать сводом), и большие круги, перпендикулярные плоскости истинного горизонта и проходящие через зенит Z и надир Z'. Они называются вертикалами, или кругами высоты. Положение любого небесного тела (на рис. II.8 обозначенного "М") определяется двумя сферическими координатами — азимутом А и высотой h. Высотой hназывают угловое расстояние от истинного горизонта, измеряемое по кругу высоты. Высота над горизонтом — положительна, под горизонтом — отрицательна. Пределы изменения высоты от -90 до +90°. Иногда вместо высоты h по кругу высоты измеряют зенитное расстояние z— угловое расстояние от зенита Z. Оно изменяется от 0° (в зените) до 180° (в надире) и всегда положительно. Значения высоты h и зенитного расстояния z одного и тoгo же небесного тела связывает простейшая формула: z=90° — h.   Вторая координата — азимут А — это угловое расстояние круга высоты от точки юга S, измеряемое по истинному горизонту по часовой стрелке, т.е. в направлении запад, север, восток, юг, в пределах от 0 до 360°. Чтобы предупредить возможные ошибки, отметим, что иногда азимут отсчитывают от точки юга S в обе стороны, считая направление к западу положительным (от 0 до +180°), к востоку — отрицательным (от 0 до -180°). Кроме того, в геодезии азимут отсчитывают от точки севера N по часовой стрелке (в направлении восток, юг, запад) в пределах от 0 до 360°. II.3.2. Экваториальная система В экваториальной системе сетка небесных координат вращается вместе с небесной сферой, поэтому координаты звезд практически не изменяются во времени. Эта система находит самое широкое распространение в звездных атласах. Рис.П.9. Экваториальная система небесных координат Экваториальная система небесных координат (рис.И.9) строится на небесном экваторе (см. рис. И.2). (Напомним, что эта плоскость совпадает с плоскостью земного экватора.) Ее координатную сетку составляют малые круги, параллельные плоскости небесного экватора, — суточные (или небесные) параллели, и большие полукруги, перпендикулярные небесному экватору — круги склонения (или часовые круги).  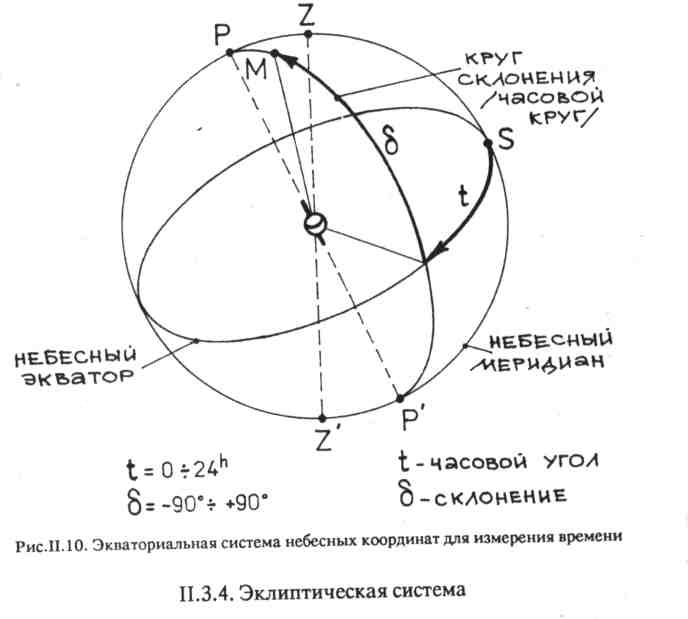 Любое небесное тело М находится на каком-либо круге скло-| нения и небесной параллели, и его положение определяется двумя сферическими координатами — прямым восхождением а и скло нением /сигма/. 1 Склонение д — это угол между направлением на небесное тело и плоскостью небесного экватора, измеряемый по кругу склонения. В северном полушарии небесной сферы склонение д положительно, в южном — отрицательно. Таким образом, величина склонения у различных небесных тел изменяется от +90 до -90°. (Для Полярной звезды д= +90°). Прямое восхождение а отсчитывают от точки весеннего равноденствия /Овен / в сторону против суточного вращения небесной сферы и измеряют в пределах от 0 до 360° (либо в единицах времени от 0 до 24 часов). П.3.3. Экваториальная система для измерения времени В данной системе координатная сетка та же, что и в описанной выше, а из двух сферических координат сохранена лишь одна. Причина в том, что для счета времени необходима сферическая координата, которая в ходе суточного вращения небесной сферы изменялась бы равномерно. В качестве этой координаты принят часовой угол t(рис. 11.10). Его отсчитывают от южной части небесного меридиана в направлении суточного вращения неба до круга склонения (часового круга), на котором лежит небесное тело М. За сутки часовой угол небесного тела М изменяется в пределах от 0 до 24 часов. Реже этот угол измеряют не часовой, а угловой мерой в пределах от 0 до 360°. Вторая небесная координата — склонение д . Склонение измеряется в пределах от -90 до +90°. Эта система координат — основа первых звездных атласов. И сегодня для решения многих задач именно ей астрологи отдают пред-почтение. Эклиптическая система (рис. ИЛ 1) строится на плоскости эклиптики (см. рис. И.6). Ее координатную сетку составляют малые круги, параллельные плоскости эклиптики и называемые кругами равной широты, и большие круги, перпендикулярные плоскости эклиптики и проходящие через полюса эклиптики. Большие круги называют кругами широты. Положение небесного тела определяется двумя сферическими координатами — эклиптической долготой (или просто долготой) L и эклиптической широтой (или просто широтой) В. Эклиптическая  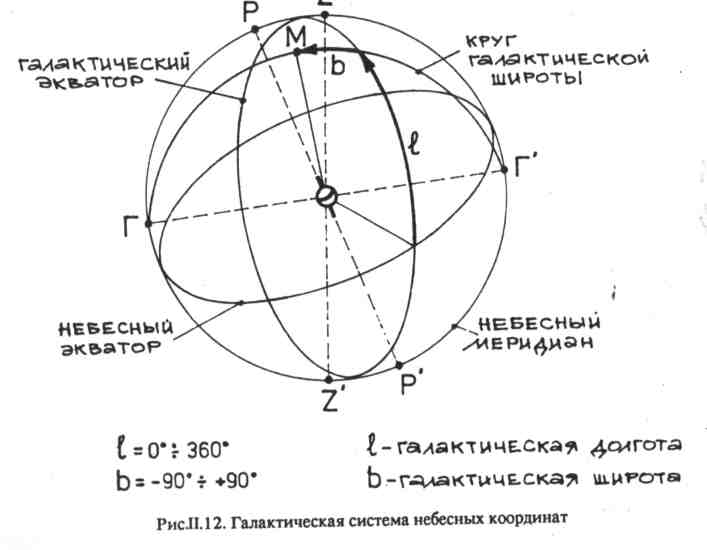 долгота Lотсчитывается от плоскости, проходящей через полюса эклиптики и точку весеннего равноденствия /овна/ в направлении годичного движения Солнца, т.е. по ходу знаков Зодиака. Долгота L измеряется в пределах от 0 до 360°. Эклиптическая широта В — это угловое расстояние от эклиптики, измеряемое по кругу широты. Значение В положительно в сторону северного полюса эклиптики и отрицательно в сторону южного. Пределы изменения эклиптической широты от -90 до +90°. ІІ.3.5. Галактическая система Эта система используется для изучения нашей галактики. Галактическая система небесных координат строится на галактическом экваторе — плоскости симметрии Млечного Пути. Координатную сетку составляют малые круги, параллельные плоскости галактического экватора, и большие круги, перпендикулярные ей и проходящие через полюса галактики. Положение небесного тела определяется двумя сферическими координатами — галактической долготой 1 и галактической широтой b (рис. 11.12). Галактическая широта Ь отсчитывается к северу от экватора галактики со знаком "+", а к югу — со знаком "-". Таким образом, пределы ее изменения от -90 до +90°. Галактическая долгота 1 отсчитывается в направлении возрастания прямых восхождений от плоскости, проходящей через полюса галактики и точку пересечения экватора галактики с небесным экватором. Пределы ее изменения — от 0 до 360°. II.4. Географические координаты Положение точек на земной поверхности определяется географической долготой и географической широтой. В сетке географических координат через полюса Земли проводят большие круги — географические меридианы, а параллельно плоскости земного экватора — малые круги, называемые географическими параллелями. За начальный или нулевой принят Гринвичский меридиан, на котором находится астрономическая обсерватория вблизи Лондона. Географическая долгота Xотсчитывается вдоль экватора к востоку от Гринвичского меридиана со знаком "+" и к западу — со знаком "-". Географическая широта учитывается вдоль меридианов в направлении географических полюсов со знаком "+" к северу и со знаком"-" к югу от экватора. Географическая широта принимает значения от -90 до +90" а долгота — от -180 до +180° (рис. 11.13). Иногда географическую долготу измеряют в единицах времени от 0 до 24 часов, причем отсчитывают ее только в одном направлении — к востоку от Гринвича. Перевод угловых единиц в единицы времени проводят из расчета: 360° = 24 часа; 1 градус =4 минуты; 1мин= 4 секунды; 1 час - 15°; 1 минута= 15'; 1 секунда - 15". 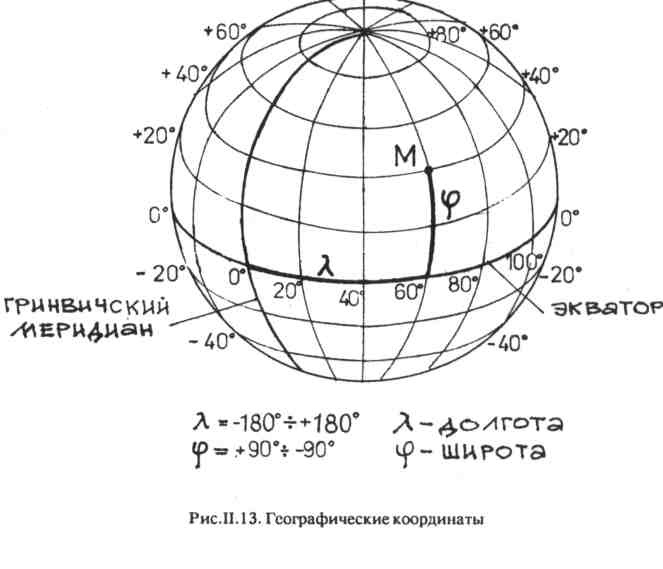 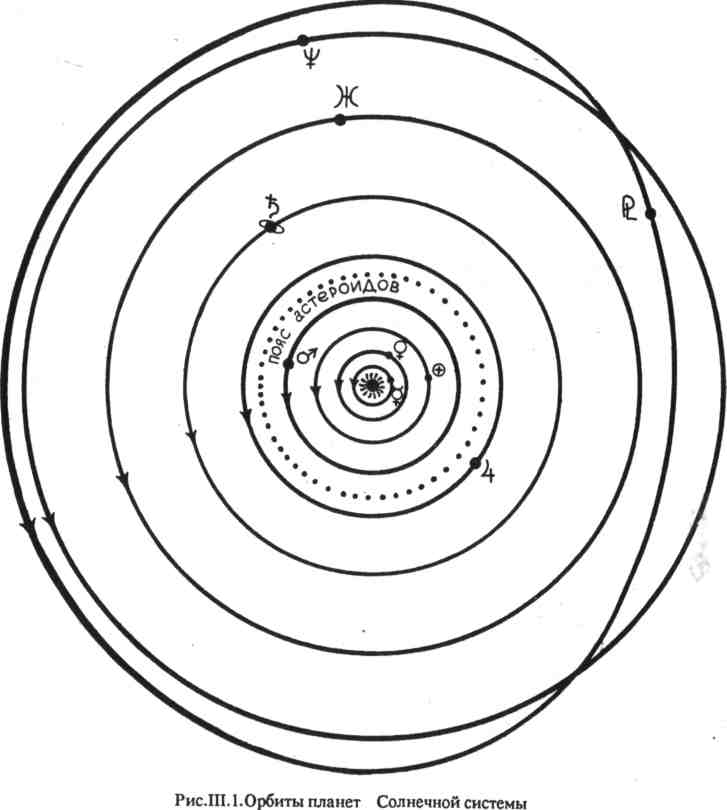 Ш. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ Наша Земля вместе с другими планетами вращается вокруг Сол-нца. Ближайшая к Солнцу планета — Меркурий. Далее, по мере удаления от Солнца, следуют Венера, Земля, Марс, Юпитер, Сатурн Уран, Нептун, Плутон. Орбиты этих планет лежат вблизи одной плоскости, называемой плоскостью эклиптики. Кроме планет, Солнечная система включает тысячи астероидом иногда называемых малыми планетами, множество комет и миллионы метеорных и метеоритных тел. Астероиды — это твердые глыбы неправильной формы. (Лишь у четырех самых крупных форма близка к щарообразной). Большинство из них движутся вокруг Сол-нца между орбитами Марса и Юпитера, образуя пояс астероидов. По своим физическим характеристикам планеты Солнечной системы делятся на две группы. Планеты, расположенные между Солнцем и поясом астероидов — Меркурий, Венера, Земля, Марс,-земная группа планет. Они невелики по размерам и массе, имею-твердую поверхность и довольно высокую плотность и, кроме Мер курия, обладают атмосферами. Планеты, движущиеся за кольцом астероидов, образуют группу планет-гигантов: Сатурн, Уран, Не-птун. Они представляют собой газообразные тела, сжатые пол гигантским давлением. Данные о последней обнаруженной к сегод-няшнему дню планете — Плутоне — неполны. Все планеты, включая Землю, обращаются вокруг Солнца и одном направлении, которое мы будем называть прямым (рис. III.1 масштабы искажены). Размеры планетной системы огромны. Ее диаметр около 12 млрд км, а самая удаленная планета Плутон отстоит от Солнца в 40 paз дальше, чем земля, Относительные средние расстояния планет от Солнца и периоды их обращения представлены в табл. III. 1. Великий математик и астроном Иоганн Кеплер вывел законы, описывающие орбитальное движение планет: П  ланеты в своем движении вокруг Солнца описывают эллипс, причем Солнце находится в одном из фокусов этого эллипса. ланеты в своем движении вокруг Солнца описывают эллипс, причем Солнце находится в одном из фокусов этого эллипса.Прямая линия, соединяющая планету с Солнцем, так называемый радиус-вектор планеты, описывает равные площади в равные промежутки времени. Следствие из этого закона — непостоянство скорости движения планет по орбите. Квадраты периодов обращения любых двух планет соотносятся между собой как кубы их средних расстояний от Солнца. III. 1. Относительные средние расстояния планет от Солнца и периоды их обращения
| ||||||||||||||||||||||||||||||||||||||||||
