Вайсберг_Астрономия для астрологов-1. В. А. Астрономия для астрологов в 3х частях. М. Цаи, 1992. 87 с. Isbn 5866610078 Эта книга
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
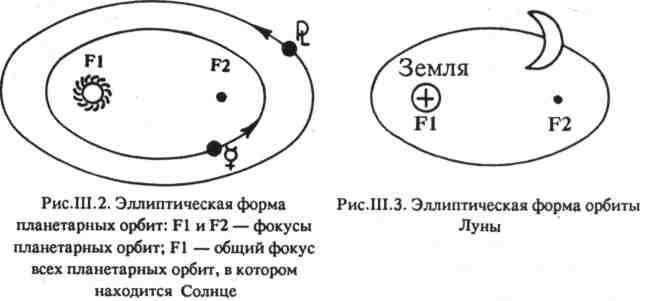 Орбиты всех планет имеют один общий фокус, находящийся в центре Солнца (рис. Ш.2). Эллиптическую форму имеет и орбита Луны — спутника Земли. В одном из фокусов этого эллипса находится Земля (рис. Ш.З). 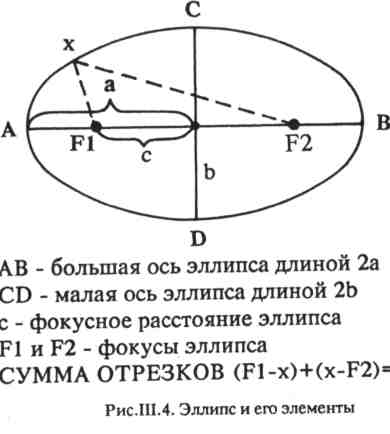 Можно нестрого определить эллипс как сплюснутую окружность, но лучше воспользоваться математическим определением: эллипс — это плоская замкнутая кривая, для любой точки которой сумма расстояний от двух фокусов постоянна и vравна длине большой оси эллипса (рис. Ш.4). Степень вытя-нутости эллипса характеризуется эксцентриситетом е - с/а. Значение эксцентриситета меняется от 0 до 1. При е - 0 эллипс превращается в окружность, а при е- 1 — в разомкнутую кривую — параболу, имеющую лишь один фокус. Все планеты Солнечной системы, кроме Меркурия и Плутона, имеют маленькие эксцентриситеты, т.е. движутся по орбитам, близким к правильным окружностям. Орбиты самой ближней к Солнцу и самой удаленной от него планет более вытянуты (см. табл. III.2). Данные таблицы показывают, что наиболее близкие к окружности орбиты имеют Венера и Нептун. Еще древние астрономы и астрологи знали, что планеты, перемещаясь по звездному небу 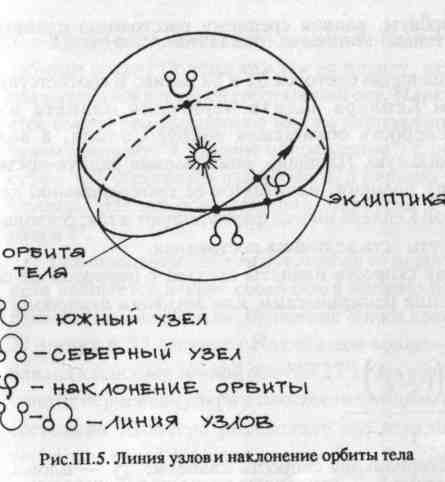 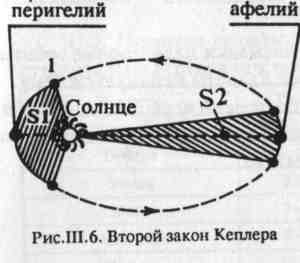 111,2. Эксцентриситеты и наклон орбит планет Солнечной системы
вблизи эклиптики, периодически удаляются от нее в обе стороны на небольшие угловые расстояния, например, Юпитер — на Г, Марс — на 2, Сатурн — на 2,5, Меркурий — на 7°. Эти удаления планет объясняются наклонением плоскостей их орбит к плоскости земной орбиты, т.е. плоскости эклиптики. Величины наклона орбит планет I представлены в табл. Ш.2, откуда видно, что наиболее приближена I к плоскости эклиптики плоскость орбиты Урана, а наиболее удалены плоскости орбит Меркурия и Плутона. Прямая линия, по которойплоскость орбиты планеты (любой, кроме Земли, чья плоскость орбиты и является плоскостью эклиптики) пересекается с плоскостью эклиптики, называется линией узлов орбиты, а точки ее пересечения с эклиптикой — узлами орбиты данной планеты. В восходящем узле планета переходит к северу от эклиптики, а в нисходящем — к югу от нее (рис. III.5). Поэтому восходящий узел иногда называют северным,а нисходящий -южным. Вернемся к рассмотрению второго закона Кеплера. Ближай шая к Солнцу точ- ка орбиты называется перигелием1, а наиболее удаленная — афелием. . Эти точки лежат на большой оси орбиты по разные стороны от солн-ца (рис. Ш.6). Большая ось орбиты носит название линии апсид. При движении планеты вокруг Солнца ее гелиоцентрическое расстояние (радиус-вектор) постоянно изменяется. Несложно показать, что длина радиус-вектора при нахождении планеты в точке перигелия равна а(1 — е), в точке афелия а(1 + е), где а — длина большой полуоси "пери" (греч.) — около. Искаженное "апогелий", где "а п о" (греч.) — вдали.  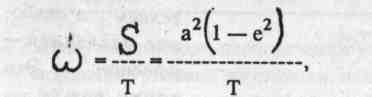 эллиптической орбиты, равная среднему расстоянию планеты от Солнца. На рис. III.6 площади секторов S1 и S2 равны. В соответствии со вторым законом Кеплера вблизи перигелия планета имеет максимальную скорость обращения вокруг Солнца, а вблизи афелия — минимальную. Площадь, описываемая радиус-вектором планеты в единицу времени, называется ее секториальной скоростью. Второй закон Кеплера иногда формулируют и так: секториаль-ная скорость планеты есть величина постоянная. Секториальная скорость планеты связана с периодом ее обращения вокруг Солнца (сидерическим, или звездным периодом) формулой: где W— секториальная скорость планеты; S— площадь ее орбиты; Т — сидерический период обращения; а — большая полуось орбиты; е — эксцентриситет. Первые два закона Кеплера описывают планетарные орбиты по отдельности, а третий связывает все планеты в единую систему. Если через Тп обозначить сидерический период обращения п-ой планеты, а через ап — ее среднее гелиоцентрическое расстояние (большую полуось орбиты планеты), то 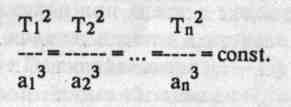 По известным периодам обращения небесных тел вокруг Солнца несложно вычислить их средние расстояния от него в относительных единицах (см. табл. III. 1). Кроме поступательного движения планет по их эллиптическим орбитам вокруг Солнца каждая из планет, включая Землю и Луну, вращается вокруг своей собственной оси. Меркурий медленно вращается вокруг оси вращения в том же направлении, что и Земля (далее будем говорить "в прямом направлении") с периодом 58,65 земных суток, что составляет примерно 2/3 периода его обращения вокруг Солнца* Наклон оси вращения Меркурия к плоскости его орбиты равен 7°. Ось вращения Венеры отклонена от перпендикуляра на 3°. Планета вращается вокруг своей оси в направлении, обратном направлению вращения Земли. Вращение Марса прямое с периодом 24 часа 37 минут и 23 секунды. Наклон оси вращения Марса (24е 48') близок к наклону земной оси (23°27'). Ось вращения Юпитера отклонена от перпендикуляра к плоскости его орбиты на 3°7\ Газообразное состояние Юпитера определяет его зональное вращение. Экваториальная зона вращается с периодом 9 часов 50,5 минут, а умеренные зоны — несколько медленнее — 9 часов 55,7 минут. Быстрым
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
