В. А. Нахалов Моделирование радиоэлектронных схем
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
|
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения» Кафедра «Телекоммуникации» В.А. Нахалов Моделирование радиоэлектронных схем Лабораторный практикум Хабаровск Издательство ДВГУПС 2008 УДК 621.38 (075.8)ББК З 844.1 я 73 Н 349 Рецензент: Доктор технических наук, заведующий кафедрой «Автоматика и телемеханика» Дальневосточного университета путей сообщения А.И. Годяев Нахалов, В.А. Н 349 Моделирование радиоэлектронных схем: лабораторный практикум / В.А. Нахалов. – Хабаровск : Изд-во ДВГУПС, 2008. – 24 с.: ил. Лабораторный практикум соответствует ГОС ВПО направления 190400 «Системы обеспечения движения поездов» специальности 190402 «Автоматика, телемеханика и связь на железнодорожном транспорте» по дисциплине «Каналообразующие устройства». Рассмотрены вопросы моделирования радиоэлектрических схем с использованием пакета программ Electronic Workbench. Предназначен для студентов 3 курса всех форм обучения, изучающих курс «Каналообразующие устройства железнодорожной автоматики, телемеханики и связи». УДК 621.38 (075.8)ББК З 844.1 я 73 © ГОУ ВПО «Дальневосточный государственный  университет путей сообщения (ДВГУПС), 2008 университет путей сообщения (ДВГУПС), 2008ВВЕДЕНИЕ В каналообразующих устройствах систем связи преобразователи спектров играют важную роль. Ранее используемые нелинейные приборы (диоды и транзисторы) в процессе преобразования дают широкий спектр гармоник, что заставляет применять сложные фильтры. Поэтому параметрические элементы и, в первую очередь аналоговые перемножители получили широкое распространение в приемо-передающей аппаратуре в качестве модуляторов, демодуляторов, преобразователей частоты. В предлагаемый лабораторный практикум включен цикл лабораторных работ и исследований радиоэлектронных схем, выполненных на моделях аналоговых перемножителей, предложены задания для студенческих научных работ. 1. Аналоговые перемножители В радиоэлектронных цепях, кроме линейных и нелинейных, широко используются параметрические цепи – это цепи, в которых хотя бы один из коэффициентов (параметров) зависит от времени. Примером такой цепи может служить усилители с управляемым коэффициентом усиления, изменения барьерной емкости p-n перехода под действием напряжения и т. д. Из курса электроники известно, что коэффициент усиления пропорционален крутизне транзистора и сопротивлению нагрузки, т. е. Если один из параметров схемы S или R изменять внешним воздействием от отдельного входа т 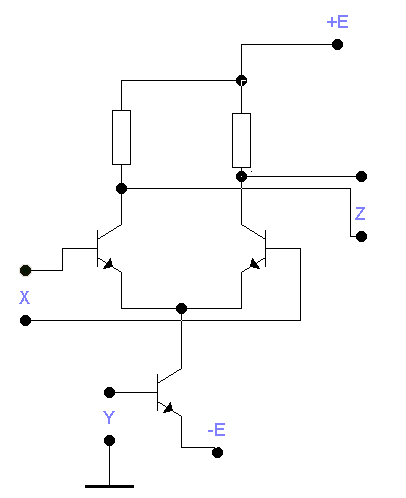 Рис. 1. Перемножитель на дифференциальном усилителе . е. получаем идеальный перемножитель. Основным элементом современного аналогового перемножителя является дифференциальный усилитель (ДУ), в состав которого включен управляемый источник тока в цепи эмиттеров. Дополнительный входной сигнал Y подается на базу транзистора источника тока. При этом изменяется ток источника тока, изменяются токи эмиттеров транзисторов ДУ. При изменении токов эмиттеров транзисторов ДУ пропорционально изменяется их крутизна, а следовательно и коэффициент передачи (усиления) ДУ по входу X. В итоге получим перемножение сигналов подаваемых на входы X и Y. Отметим, что в рассмотренной схеме напряжение на входе Y должно быть только положительным, в противном случае транзистор генератора стабильного тока закроется, и коэффициент передачи схемы по входу X будет равен нулю. Для обеспечения работы перемножителя при любом знаке напряжения на входе Y в схеме вводят дополнительные элементы, которые образуют дифференциальный усилитель из двух источников тока, поэтому на вход Y можно подавать напряжение любой полярности. Такие перемножители называются четырехквадрантными. Этим названием подчеркивается возможность их работы, как с положительным, так и с отрицательными напряжениями на любом из входом. Примером может служить интегральная микросхема KР525ПСIA (зарубежный аналог АД532), предназначенная для работы в радиоэлектронной аппаратуре в качестве аналогового перемножителя сигналов с регулируемым масштабным коэффициентом. В десятой и восьмой версиях EWB имеется ее модель. Во всех версиях, включая EWB 5.12, имеется идеальная модель, которая также через диалоговое окно позволяет устанавливать коэффициенты усиления по входам X и Y, и общий коэффициент усиления, а так же устанавливать постоянные составляющие. Рассмотрим пример. Имеется источник У  словное обозначение перемножителя приведено на рис. 2. словное обозначение перемножителя приведено на рис. 2.2. МОДУЛЯТОРЫ 2.1. Амплитудные модуляторы Процесс, при котором амплитуда высокочастотных колебаний изменяется по закону управляющего сигнала, носит название амплитудной модуляции (АМ). В простейшем случае выражение для АМ сигнала будет иметь вид На вход X перемножителя поступает модулирующее (гармоническое) низкочастотное напряжение 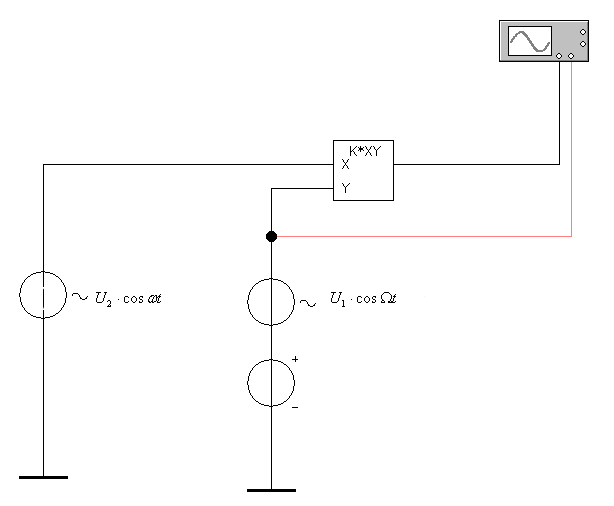 Рис. 3. Схема амплитудного модулятора На второй вход Y перемножителя поступает напряжение несущей Раскрывая скобки и произведя тригонометрические преобразования, получим Таким образом, произошел перенос сигнала с частотой Ω в диапазоне частоты Если не производить тригонометрических преобразований, то 2.2. Моделирование амплитудных модуляторов 1. Собрать схему, показанную на рис. 3. Установить следующие параметры. Частота несущей – 1 кГц, частота модуляции – 100 Гц. Для этого взять из библиотеки генераторы переменного напряжения, установить действующее напряжение 1 В ( 2. Исследовать зависимость коэффициента модуляции от амплитуды несущей, постоянного напряжения, амплитуды модулирующего сигнала и частоты модулирующего сигнала. Построить графики 3. Используя меню Analysis\Fourier, получить спектр исследуемого сигнала. Зарисовать амплитудный спектр, сравнить амплитуды боковых и несущей с расчетными. 4. Установить 5. Исследовать работу амплитудного модулятора, подавая на него модулирующие сигналы (например, треугольные) от функционального генератора. 6. В технике связи широко используются однополосные сигналы (сигнал ОБП – одной боковой полосы). Другая боковая и несущая на выходе отсутствуют. Идея метода фазирования достаточно проста. Пусть даны входные сигналы Записав это выражение в виде В диалоговом окне генераторов установить указанное значение действующего напряжения, частоты и начальной фазы. Все коэффициенты усиления умножителей и сумматоров принять равными единице. Запустить схему и выключить. Зарисовать осциллограмму выходного напряжения. Произвести Фурье-анализ. Повторить эксперимент для верхней боковой частоты, для чего в одном из генераторов несущей изменить фазу на 180°. 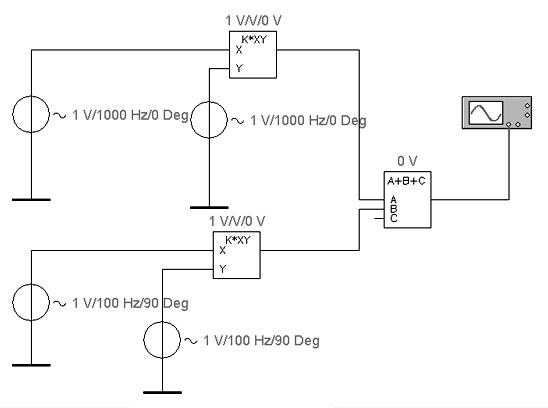 Рис. 4. Модулятор ОБП-сигнала 2.3. Частотный модулятор Для получения частотной модуляции нужно, чтобы частота колебаний генератора несущей изменялась под действием управляющего сигнала Изменение частоты генерируемых колебаний может быть достигнуто изменением одного из реактивных элементов контура (L или С). Для осуществления частотной модуляции параллельно контуру подключают параметрический элемент, реактивное управляемое сопротивление которого изменяется под воздействием модулирующего сигнала Рассмотрим случай, когда в качестве сопротивления В этом случае частота генерируемых колебаний определяется как 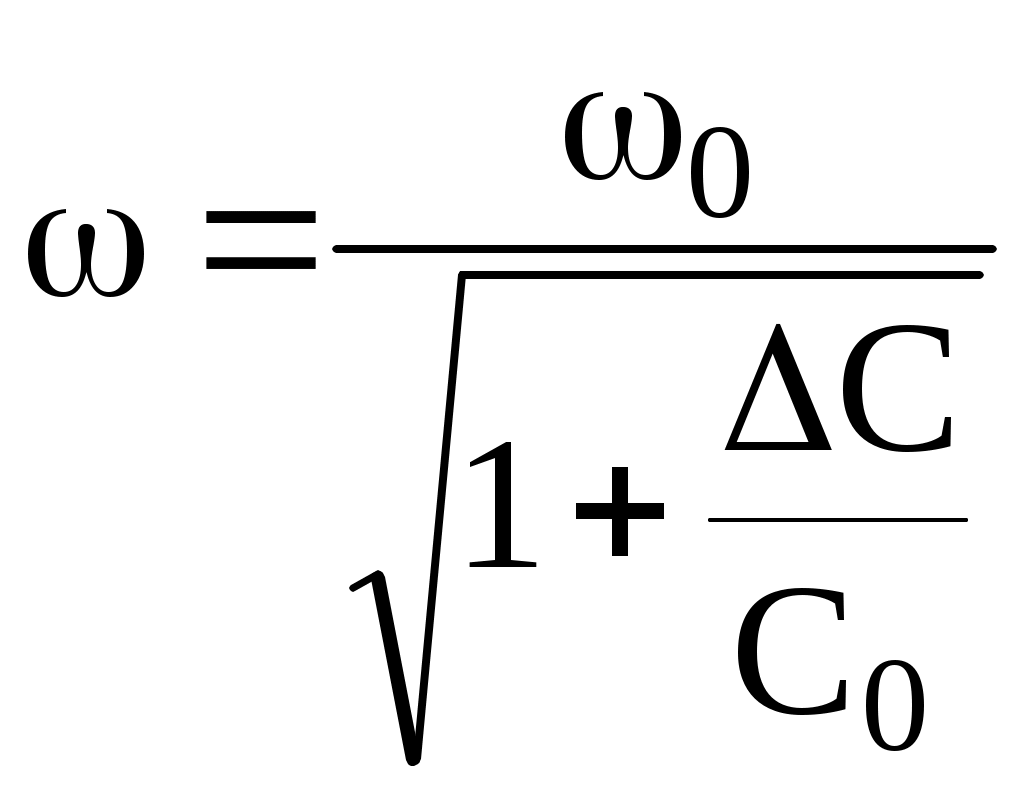 . Изменение общей емкости контура на величину . Изменение общей емкости контура на величину 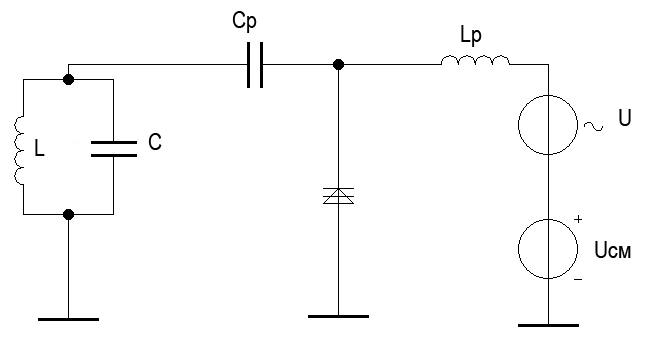 Рис. 5. Схема подключения варактора Продифференцировав выражение резонансной частоты, получим Таким образом, если относительное изменение емкости (или индуктивности) невелико, то оно вызывает пропорциональное изменение частоты генерируемых колебаний. Практическая схема управляемой емкости, влияющей на частоту генератора, приведена на рис 6. Она будет использоваться в модели ЧМ-генератора. 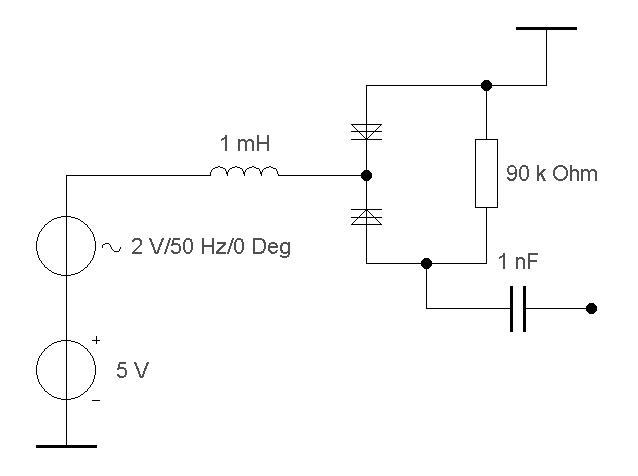 Рис. 6. Схема включения варакторов Емкость 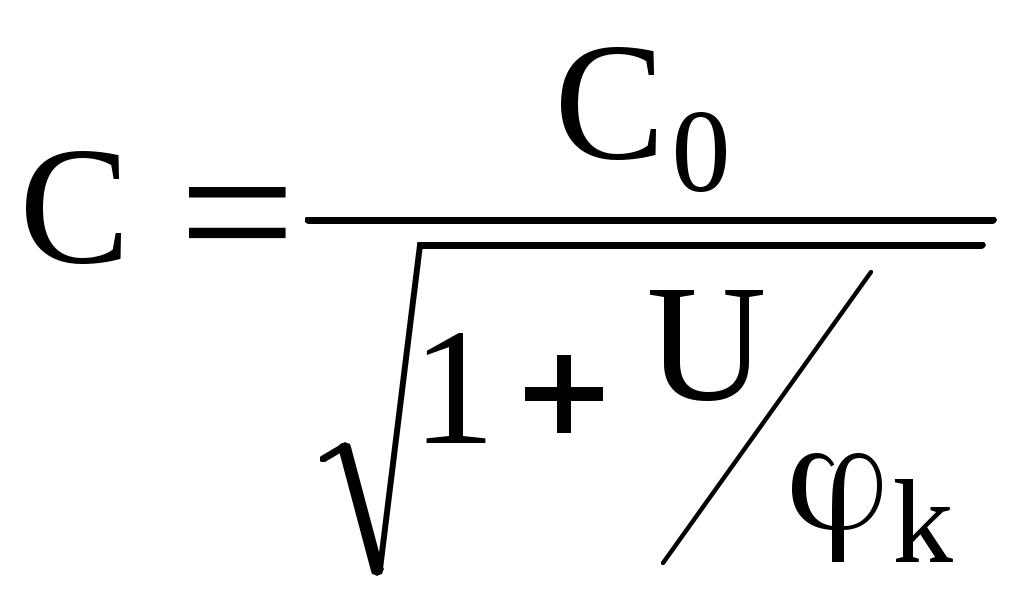 , где , где По этим данным можно определить отклонение емкости 2.4. Исследование частотного модулятора Собрать схему, показанную на рис. 7. Модулирующий блок отключить (клавишей Space). Измерить по осциллограмме период и определить частоту. Подключить к выходу генератора ЧМ-детектор и убедиться в отсутствии НЧ-колебаний. Подключить модулирующий блок. Установить Использую меню Analis\Fourier, получить спектры ЧМ-колебаний для 5. Используя параметры варактора и номинальные величины элементов схемы рассчитать девиацию  Рис. 7. Исследование частотного модулятора 2.5. Фазовый модулятор Для осуществления фазовой модуляции (ФМ) нужно иметь устройство, на выходе которого фаза колебаний изменяется пропорционально модулирующему сигналу. Как известно, ФМ и ЧМ связаны между собой: изменение частоты во времени по закону Другой способ получения ФМ основан на преобразовании АМ-колебания в ФМ-колебания. При осуществлении ФМ получается колебания Это выражение можно получить, если перемножить 2.6. Исследование фазового модулятора 1. Собрать схему, показанную на рис 8.  Рис. 8. Схема фазового модулятора 2. Установить для перемножителя Кх = Ку = 1, Квых = 2, для сумматора Ка = Кс = Квых = 1. 3. Изменяем амплитуду модулирующего напряжения (F = 1 кГц) от 0,1 В до 0,6 В (шаг 0,1 В), измерить фазовый сдвиг выходного сигнала по отключению генератора 2V/10kHz/90 Deg. Обратить внимание на появление паразитной амплитудной модуляции. Отметить амплитуду модулирующего напряжения, при котором появляется паразитная АМ. 4*. Предложить схему ФМ модулятора, в которой АМ модуляция сведена к минимуму. |
