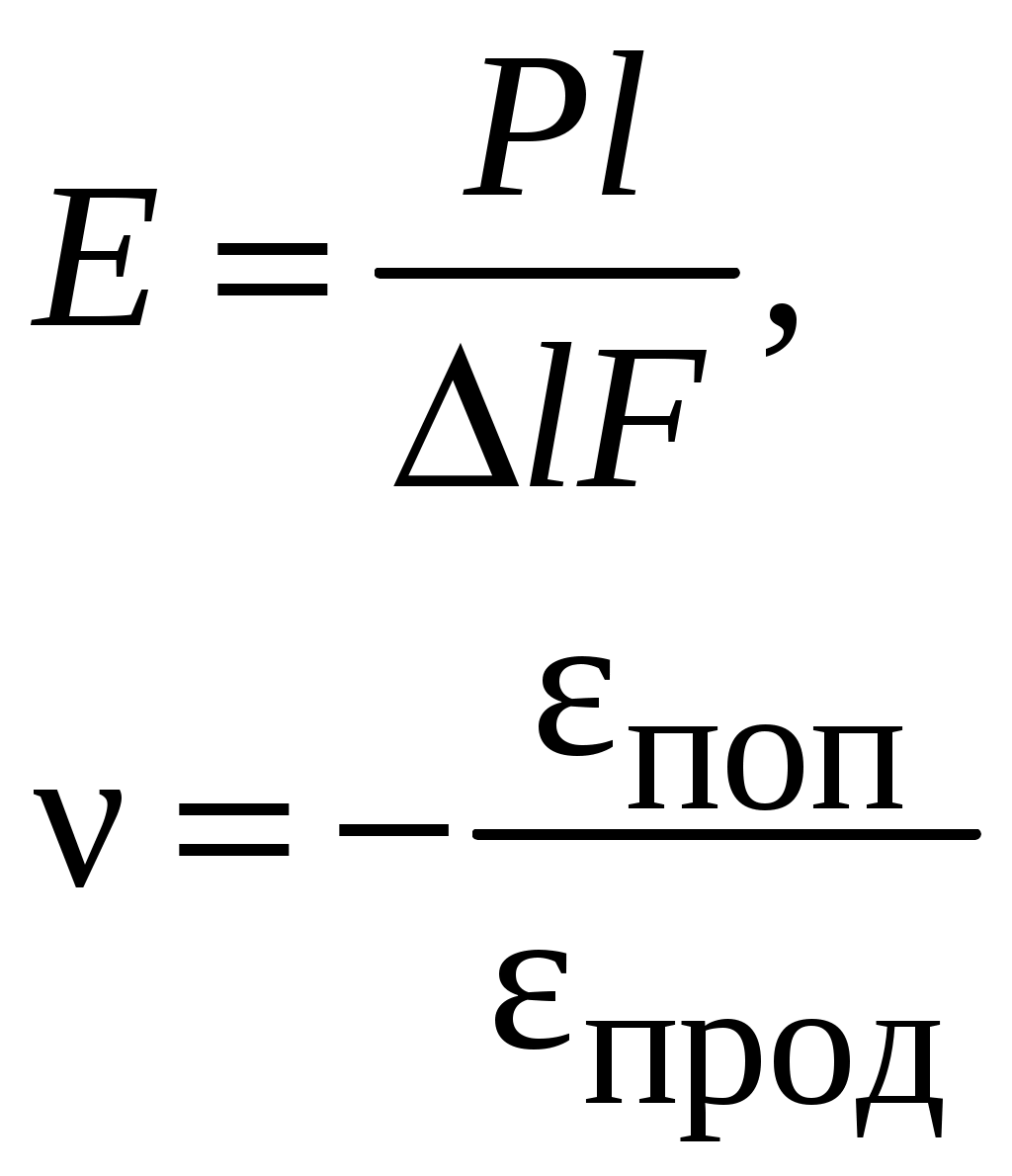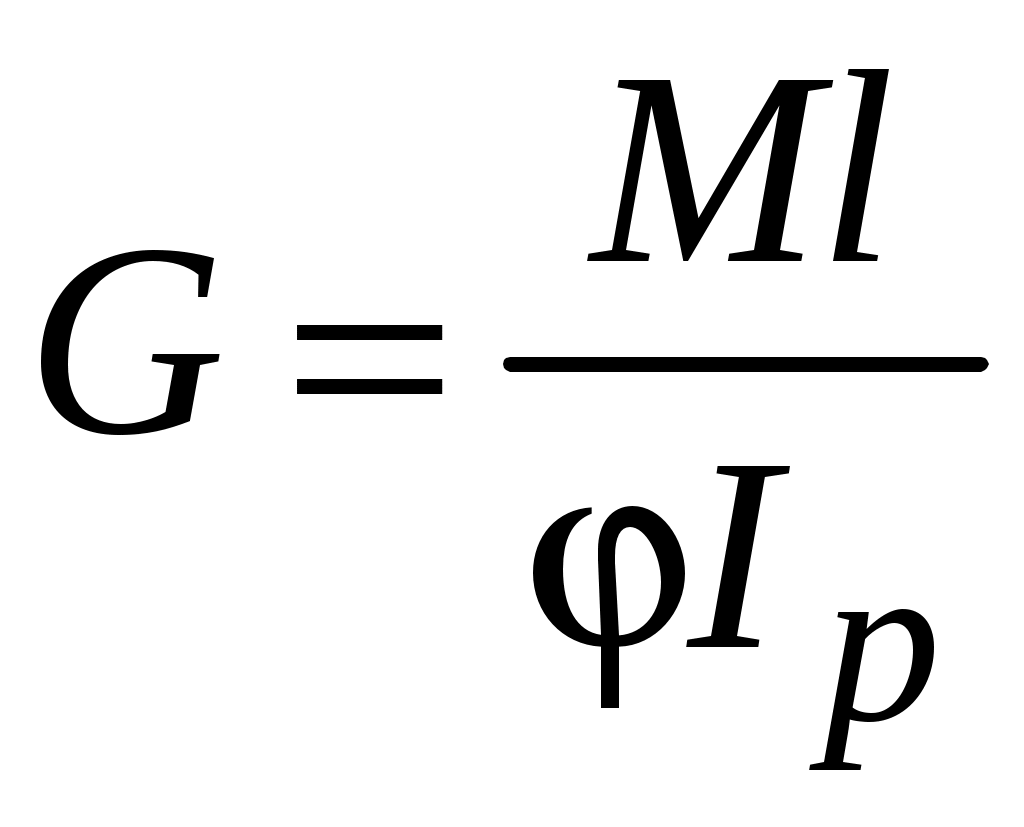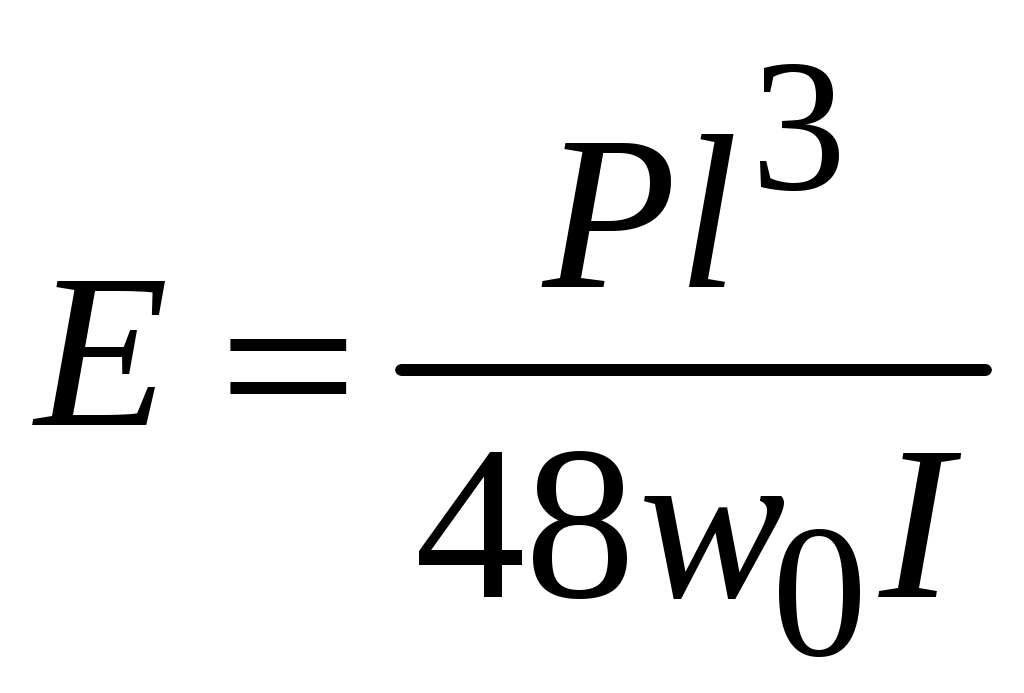Лабораторная работа 2 ТОЭ. В. И. Ульянова (Ленина) методы определения механических свойств материалов учебнометодическое пособие
 Скачать 7.97 Mb. Скачать 7.97 Mb.
|
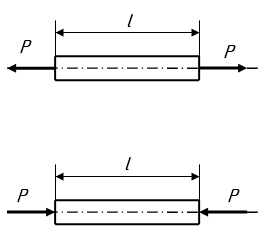
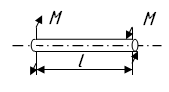
1 2 МИНОБРНАУКИ РОССИИ  Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина) МЕТОДЫ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВУчебно-методическое пособие Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ» 2  017 017УДК 621.396(075.8) ББК 31.23я73 М55 Авторы: Ю. А. Шукейло, С. К. Степанов, Е. Ю. Белова, Т. С. Липьяйнен, А. И. Лысков. М55 Методы определения механических свойств материалов: учеб.-метод. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2017. 32 с. ISBN 978-5-7629-2071-1 Содержит основные теоретические сведения и методики проведения лабораторных работ по определению механических свойств материалов. Предназначено для студентов дневной и вечерней форм обучения технических факультетов университета, изучающих дисциплину «Конструкционные и биоматериалы». УДК 621.396(075.8) ББК 31.23я73 Рецензент: канд. техн. наук, зав. кафедрой технической механики и инженерной графики ФГБОУ ВО СПХФА Минздрава России Л. М. Ображей. Утвержденоредакционно-издательским советом университетав качестве учебно-методического пособия ISBN 978-5-7629-2071-1  © СПбГЭТУ «ЛЭТИ», 2017 © СПбГЭТУ «ЛЭТИ», 2017Лабораторная работа № 1 ОПРЕДЕЛЕНИЕ МОДУЛЕЙ УПРУГОСТИ МАТЕРИАЛА РЕЗОНАНСНЫМ МЕТОДОМ Цель работы: ознакомление с методикой измерения и приобретение практи-ческих навыков определения модулей упругости материала (модуля Юнга) с по-мощью прибора типа «Звук»; определение относительной погрешности измерений. 1.1. Общие сведения Модули упругости являются фундаментальными физическими величинами, характеризующими механические свойства материалов. Их измерение весьма важно при изучении физико-механических свойств вещества. Модули упругости входят в качестве коэффициентов в соотношения, связывающие напряжения и деформации в твердом теле, и используются в расчетах напряженно-деформированного состояния этих тел. У большинства конструкционных материалов при малых деформациях связь между напряжениями и деформациями является линейной и выражается законом Гука. В случае изотропных материалов закон Гука имеет следующий вид: 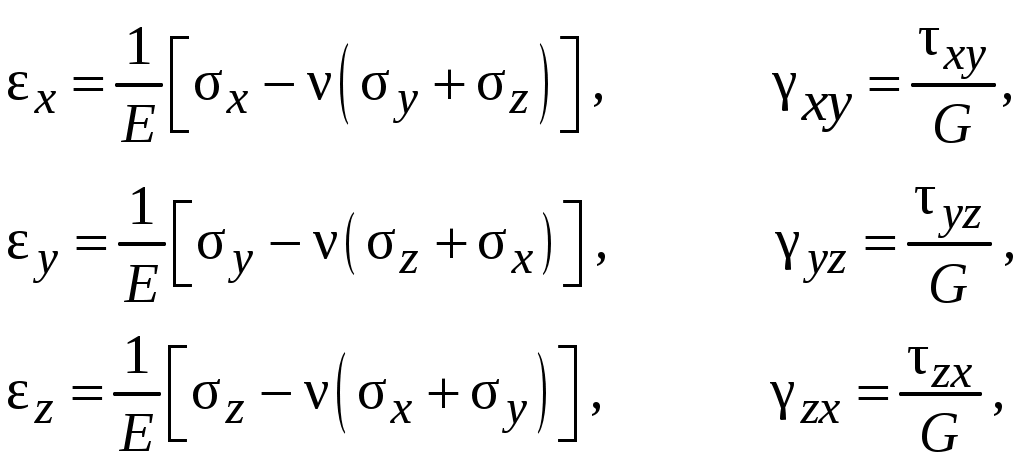 где Из трех величин E, ν, G – независимых только две, так как имеет место соотношение 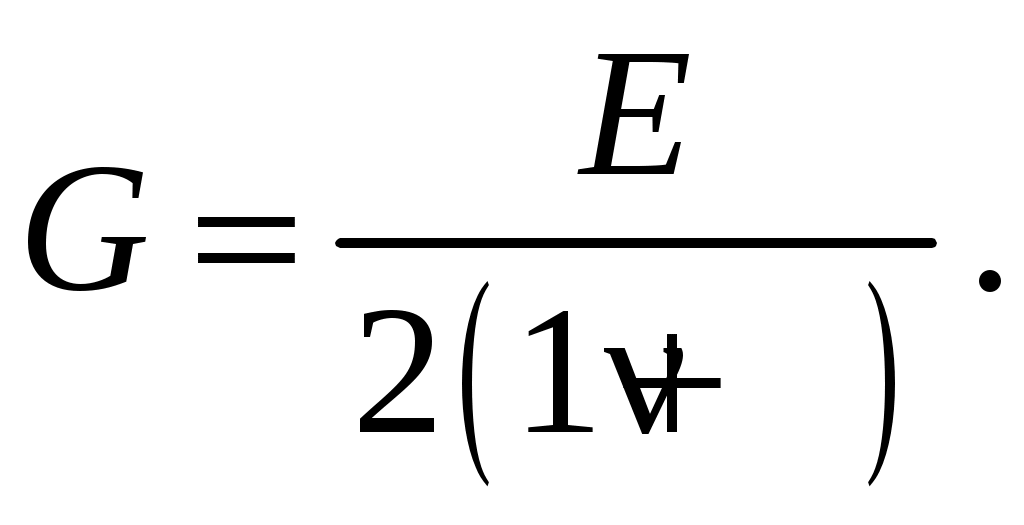 (1.1) (1.1)Модули упругости определяются экспериментально. Методы определения модулей разделяются на статические и динамические. Их существенное различие состоит в том, что в статических методах образец подвергается неизменному (или медленно изменяющемуся) во времени воздействию (статическое испытание), а в динамических методах воздействие является переменным во времени (периодическим), причем частота его такова, что длина возбуждаемой в образце упругой волны меньше или, по крайней мере, сравнима с его характерным размером (упругой волной называются распространяющиеся в среде с некоторой конечной скоростью упругие деформации). Модули упругости зависят от внешних факторов, в частности, от температуры. Как правило, с повышением температуры модули E и G уменьшаются, а коэффициент Пуассона увеличивается, приближаясь к 0,5. Влияние температурного фактора на модули упругости необходимо учитывать при расчете конструкций, поэтому измерение модулей упругости проводят при различных, в частности при весьма высоких (до 2000 °С) температурах. При статических испытаниях наиболее просто модули упругости определяются при растяжении (сжатии), кручении и изгибе стержней (таблица). Определение модулей упругости
Примечания: 1. Обозначения в формулах: F – начальная площадь поперечного сечения образца; 2. Звездочкой отмечены номера стандартов, которые регламентируют определение модулей упругости. На значение модулей упругости, определяемых статическими методами (статическое испытание обычно продолжается 5...10 мин), оказывает влияние ползучесть материала (ползучесть – возрастание деформаций с течением времени при постоянном уровне напряжений; рис. 1.1: У металлов ползучесть существенна лишь при высоких температурах, у высокополимерных материалов (пластмассы, резина, каучук) ползучесть заметна и при комнатных температурах. 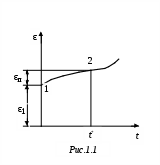 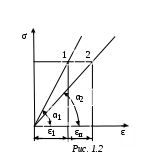 При статических испытаниях «мягких» материалов (получающих большие деформации при малых нагрузках) трудно оставаться в пределах чисто упругой деформации без частичного перехода в пластическую область (рис. 1.3, точка 2); это ведет к кажущемуся снижению модулей Eи G, 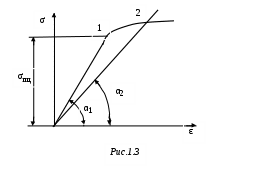 От указанных недостатков свободны динамические методы, в которых величины напряжений и деформаций и время протекания процессов весьма малы и поэтому не возникают пластические деформации и не успевают развиться деформации ползучести. Следовательно, динамические методы являются более точными, чем статические. Существенные трудности возникают при использовании статических методов для определения модулей упругости весьма хрупких материалов, например, керамики, так как приходится измерять чрезвычайно малые перемещения. Динамические методы определения модулей упругости основаны на связи последних со скоростью упругих волн, которая прямо или косвенно измеряется в исследуемом образце. Рассмотрим явление распространения волн в упругих телах на примере продольной волны, распространяющейся в тонком полубесконечном призматическом стержне. Пусть к торцу стержня внезапно приложена постоянная сжимающая сила (рис. 1.4). В первый момент сила Р вызовет сжатие бесконечно малого элемента, непосредственно примыкающего к торцу. Это сжатие передается следующему элементу и т. д., причем этот процесс будет постепенно (не мгновенно) развиваться во времени. В момент времени t сжатой будет лишь некоторая часть длины стержня (она заштрихована на рисунке), тогда как остальная часть еще не испытывает сжатия. Обозначим через vl скорость, с которой распространяется деформация сжатия вдоль оси стержня. Тогда vlt 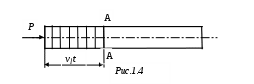 есть длина сжатого участка в момент времени t. Сечение А–А, которое служит границей между напряженной и ненапряженной частями стержня, называется фронтом упругой волны, этот фронт движется со скоростью vl. Распространение волны можно трактовать как движение фронта волны. В соответствии с законом Гука укорочение сжатой части равно Рvlt/ЕF. Это выражение также определяет перемещение торца стержня в рассматриваемый момент времени, следовательно, скорость движения торца определяется выражением С этой же скоростью движутся все частицы, принадлежащие сжатой части, причем скорость v во много раз меньше скорости vl, так как в упругом состоянии P/F << Е. Применим для сжатой части стержня теорему о количестве движения. В течение времени t на нее действует сила Р, следовательно, импульс силы равен Pt. В начальный момент времени вся выделенная часть была в покое, в момент t вся она движется со скоростью v, следовательно, изменение количества движения равно (ρvltF)v, где ρ – плотность; ρvltF – масса сжатой части. Приравняем импульс силы изменению количества движения, получим Из (1.2) и (1.3) находим скорость упругой продольной волны в тонком стержне: Если к концу стержня с круглым поперечным сечением приложить момент в плоскости торца, то возникнет крутильная волна, распространяющаяся вдоль стержня. Аналогично предыдущему можно получить выражение, определяющее ее скорость: В неограниченной упругой среде распространяются волны двух типов – продольные и поперечные. В продольной волне смещение частиц тела происходит в направлении распространения волны. Поперечная волна характеризуется смещением частиц в направлениях, перпендикулярных направлению распространения волны. Скорости продольной (vl) и поперечной (vt) волн в неограниченной среде определяются следующими выражениями: 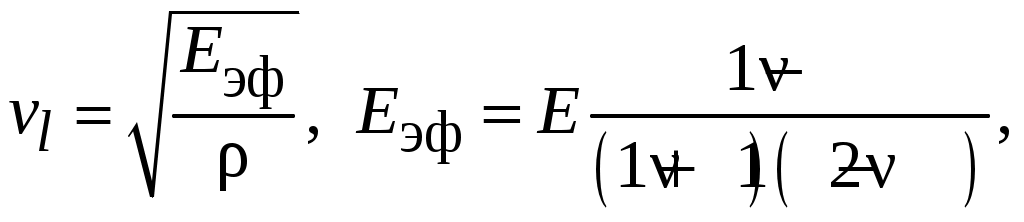 (1.5) (1.5)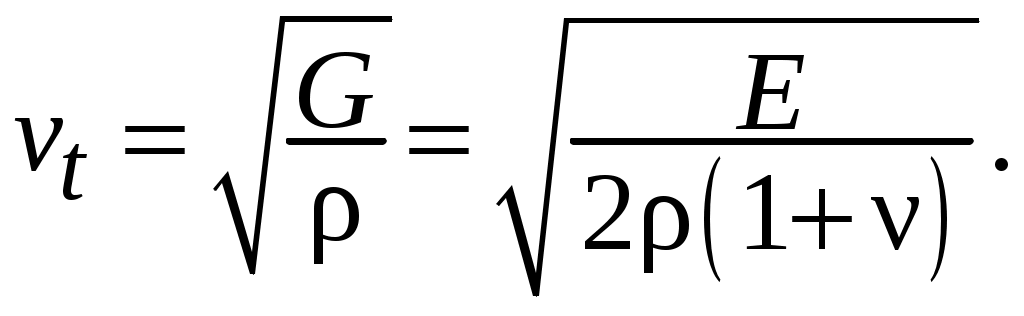 (1.6) (1.6)Скорость продольной волны в неограниченной среде больше скорости продольной волны в стержне, представляющем собой ограниченное тело. Это обстоятельство связано с тем, что в неограниченной среде поперечные (по отношению к направлению распространения волны) линейные деформации отсутствуют, и поэтому материал становится как бы более «жестким» Поперечная волна в неограниченной среде и крутильная волна в стержне представляют собой распространяющуюся деформацию сдвига, поэтому скорости этих волн определяются одинаковыми выражениями. Динамические методы определения модулей упругости можно разделить на методы, использующие непрерывные колебания, и импульсные методы. Среди первых наибольшее распространение получил резонансный метод, основанный на использовании явления резонанса в исследуемом образце, совершающем вынужденные механические колебания. Резонанс возникает при совпадении частоты вынуждающей силы с одной из частот собственных колебаний образца и характеризуется максимальной амплитудой колебаний. Обычно испытанию подвергаются образцы материала в виде тонкого призматического стержня. Рассмотрим суть резонансного метода на примере стержня (рис. 1.5), совершающего под действием внешней осевой переменной силы, приложенной к торцу стержня, продольные колебания по длине. Последние можно представить в виде наложения двух встречных продольных волн, скорость которых определяется (1.4). Из решения уравнения продольных колебаний для стержня со свободными торцами следует, что при резонансе на 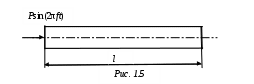 длине стержня укладывается половина длины волны или любое нечетное число полуволн, т. е. где l – длина стержня; λn – длина упругой волны; n = 1, 2, 3, ... – номер гармоники. Учитывая, что λn=vl/fn, где fn – резонансная частота гармоники с номером n,получим выражение для vl: Формулы (1.7) и (1.8) справедливы для стержней со свободными торцами. При испытаниях образец, вообще говоря, этому условию не удовлетворяет. Однако погрешность, связанная с использованием (1.8), будет тем ниже, чем меньше амплитудное значение внешней вынуждающей силы по сравнению с максимальной нормальной силой, возникающей в образце при резонансе. Обычно для измерений используется первый, самый низкочастотный резонанс (n = 1). В этом случае выражение для модуля Юнга, полученное при подстановке (1.8) в (1.4), имеет вид Таким образом, измерив плотность материала ρ, длину образца l и резо-нансную частоту f1, можно определить модуль Юнга материала образца. Аналогично, если возбудить в стержне с круглым поперечным сечением крутильные колебания, можно определить модуль сдвига G по формуле Импульсные методы измерения модулей упругости получили в настоящее время широкое применение при исследованиях физических характеристик различных материалов. Эти методы отличаются высокой точностью. Одним из главных достоинств импульсных методов является малая механическая энергия, излучаемая в исследуемую среду, благодаря чему энергетические характеристики вещества не меняются в процессе измерений. Во всех этих методах искомая скорость упругих волн определяется измерением времени распространения ультразвукового импульса на известном расстоянии. Импульсные методы подразделяются на абсолютные и сравнительные. Абсолютные методы основаны на прямом отсчете времени распространения ультразвукового импульса в образце. Сравнительные методы заключаются в сравнении времени распространения высокочастотного импульса в исследуемом образце и эталоне, скорость упругих волн в котором известна или может быть вычислена. Наиболее совершенной модификацией импульсных методов является импульсно-фазовый метод, в котором время распространения ультразвукового импульса в образце фиксируется не только по его огибающей, но и с учетом фазы его высокочастотного заполнения. Одним из широко распространенных приборов для измерения скорости упругих волн в твердых телах является ультразвуковой измеритель скорости УЗИС ЛЭТИ, в котором реализован импульсно-фазовый сравнительный метод. Измерение скорости упругих волн этим прибором основано на определении времени прямого прохождения ультразвукового импульса в измерительной линии (с образцом и без образца) по известной скорости продольной волны в жидкостной эталонной линии. Измерение скорости продольных и поперечных волн проводится на образцах, диаметр которых много больше длины упругой волны, поэтому распространение упругих волн происходит как в неограниченной среде. В этом случае скорости волн связаны с модулями упругости соотношениями (1.5) и (1.6). Решая (1.5) и (1.6) относительно E и ν получим: 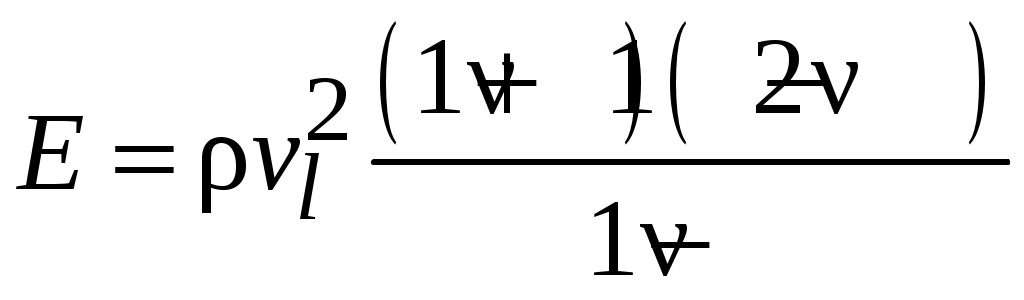 , (1.10) , (1.10)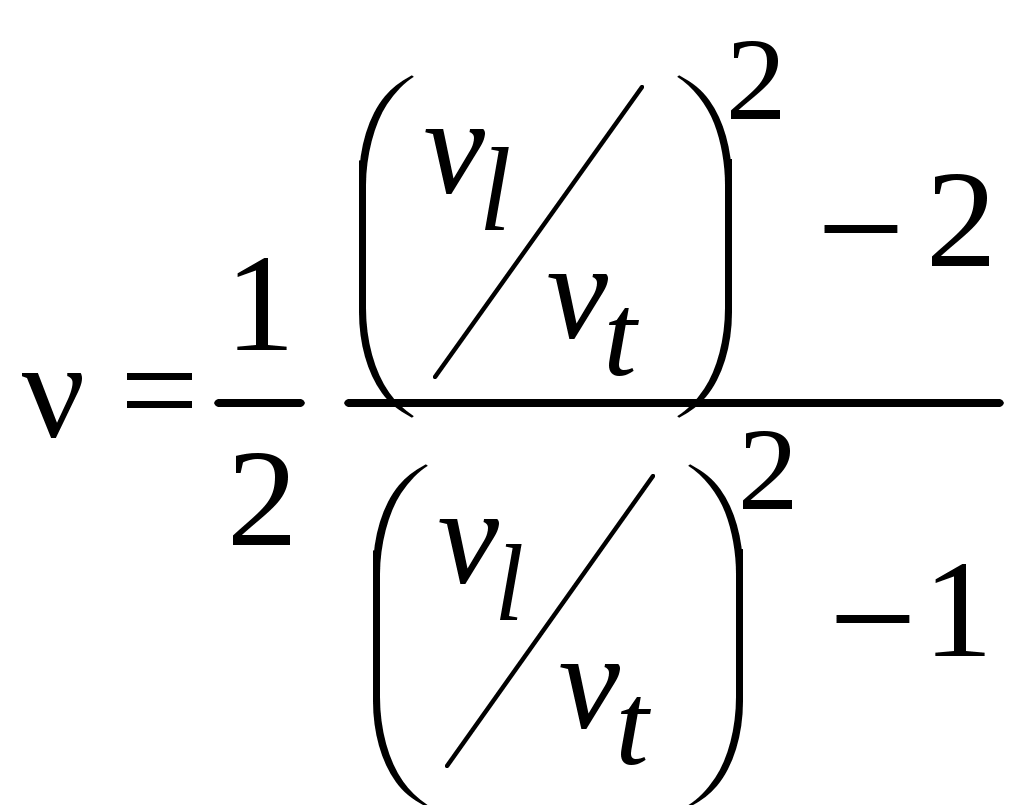 . (1.11) . (1.11)Из (1.8) – (1.11) видно, что точность определения модулей E и ν зависит от точности измерения скоростей vl и vt. Измерение этих скоростей может быть осуществлено с большей точностью, чем измерение перемещений в статических методах. Поэтому точность определения модулей упругости в динамических методах выше, чем в статических (примерно на порядок). Поскольку скорость упругих волн в материале и его физико-механичес-кие характеристики определяются в значительной степени микроструктурой материала, то динамические методы могут быть положены в основу неразрушающих методов контроля физико-механических свойств материалов, например, механической прочности. 1 2 | ||||||||||||||||||||||||||||||||||||||||||