В ряде важнейших областей техники нельзя обойтись без постоянного тока. Основными потребителями постоянного тока являются электролизные установки для получения алюминия, меди, цинка и других технически чистых металлов
 Скачать 5.29 Mb. Скачать 5.29 Mb.
|
|
2. Основные расчетные соотношения для анализа и сравнения выпрямителей и обоснование выбора 12-пульсной схемы выпрямления .1 Теоретическая база для определения основных характеристик, расчета и сравнения многопульсных выпрямителей Основные соотношения для анализа выпрямленного напряжения Выпрямленное напряжение относится пульсирующему типу напряжений и может быть представлено в виде суммы постоянной составляющей и несинусоидальной переменной составляющей, разлагаемой в гармонический ряд. При анализе выпрямленного напряжения, параметры которого напрямую связаны с выбранным схемным решением, при известной пульсности, при холостом ходе выпрямителя, в первую очередь определяются [4, 6]: . Мгновенное значение выпрямленного напряжения без учета падения напряжения на вентилях где КСХ - коэффициент схемы, численное значение которого зависит от схемы выпрямления; . Среднее значение выпрямленного напряжения 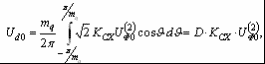 (2.2) (2.2)где D - коэффициент выпрямления, который при В режиме нагрузки среднее значение выпрямленного напряжения снижается в результате различных потерь, в том числе потерь, обусловленных коммутационными процессами, когда переключение вентильных обмоток происходит не мгновенно, а с задержкой, во время действия которой образуется контур со встречными ЭДС вентильных обмоток. В этом случае среднее значение выпрямленного напряжения где kd - коэффициент коммутации для постоянной составляющей выпрямленного напряжения, где В работе [6] отмечено, что в сложных схемах выпрямления коммутация вентильных токов осуществляется внутри отдельных секций (звеньев преобразования) независимо друг от друга. Угол коммутации зависит от схемы выпрямления, и для любой mq - пульсной схемы выпрямления значение угла коммутации определяется по выражению [5]: 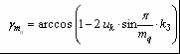 (2.6) (2.6)где Относительную величину переменной составляющей кривой выпрямленного напряжения характеризует коэффициент формы напряжения по действующему значению (волнистость кривой), определяемый по формуле [4]: 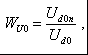 (2.7) (2.7)где Эффективное значение выпрямленного напряжения при холостом ходе выпрямителя где 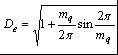 (2.9) (2.9)В режиме нагрузки волнистость кривой выпрямленного напряжения определяется как отношение эффективного значения переменной составляющей выпрямленного напряжения, полученной с учетом индуктивного сопротивления вентильных обмоток трансформатора, к среднему значению выпрямленного напряжения на холостом ходу выпрямителя 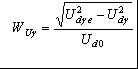 (2.10) (2.10)где где 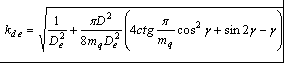 (2.12) (2.12)Таким образом, волнистость кривой выпрямленного напряжения в режиме нагрузки зависит не только от угла коммутации Гармонический анализ выпрямленного напряжения Кривая выпрямленного напряжения в режиме холостого хода выпрямителя за каждый период сетевого напряжения представляет собой 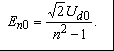 (2.13) (2.13)В режиме нагрузки действующее значение ЭДС гармоники n-го порядка определяется из выражения где 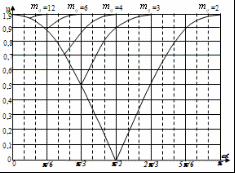 Рисунок 2.1 - Влияние пульсности выпрямителя на форму выпрямленного напряжения Связи токов на входе и выходе ТПЧФ выпрямителя и гармонический анализ сетевых токов С учетом пренебрежения токами холостого хода, что вполне приемлемо при мощном трансформаторном оборудовании, составляются уравнения магнитодвижущих сил (МДС) трансформаторов. Из решения полученных уравнений, при условии равенства нулю суммы сетевых токов и с учетом схемотехнических соотношений между числами витков первичных и вентильных обмоток, устанавливаются соотношения, связывающие токи первичной трехфазной и вторичной многофазной цепей. На интервале проводимости соответствующих вентилей, при С помощью любой подходящей компьютерной программы выполняется гармонический анализ токов первичной трёхфазной сети. Для этого период 2p разбивается на приемлемое число интервалов, достаточное для заданной точности описания кривых сетевых токов. Токи вторичных обмоток трансформаторов, приравненные к току нагрузки, представляются в виде прямоугольных форм с величиной равной 1,0. В соответствии с алгоритмом работы вентильных обмоток ФС ЭДС, эти токи трансформируются в ступенчатые формы токов для каждой сетевой фазы, которые затем разлагаются в ряд Фурье. Ступенчатость сетевых токов выпрямителя говорит о потреблении из сети несинусоидального тока. В результате разложения в ряд Фурье для ступенчатой формы токов каждой фазы находятся множества синусоидальных функций (гармоник), представляющих эту форму. Приближенные к реальным, ступенчатые фазные токи заменяются суммой синусоидальных гармоник со своими фазами в соответствии с выражениями: 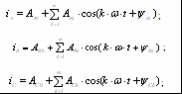 (2.16) (2.16)где Порядок высших гармоник токов питающей трехфазной сети для многопульсных выпрямителей можно определить в соответствии с двумя простыми принципами [10]. 1. Для mq-пульсного выпрямителя на входе присутствуют гармоники с порядковыми номерами где n - ряд целых чисел 1, 2, 3… . Уровень К-й гармоники обратно пропорционален ее порядковому номеру В таблице 2.1 приведены уровни гармоник mq-пульсных выпрямителей. Коэффициент пульсации в этом случае определяется В схемах выпрямления с 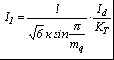 (2.20) (2.20)где Таблица 2.1 - Гармонический состав токов питающей трехфазной сети для многопульсных выпрямителей
|
