истмат. В векторном виде для жидкости они записываются следующим образом
 Скачать 249.97 Kb. Скачать 249.97 Kb.
|
|
Это может показаться удивительным, но на сегодняшний день все еще есть загадки, решить которые не удается даже великим умам. В математике таких загадок семь, и их окрестили как "Задачи тысячелетия". 1. Уравнения Навье-Стокса (1822 год) Как известно, если плыть по воде на лодке, вокруг вас необратимо возникнут волны. А если лететь на самолете, в воздухе будут возникать турбулентные потоки. Оба явления уже описаны уравнениями Навье-Стокса. В векторном виде для жидкости они записываются следующим образом: 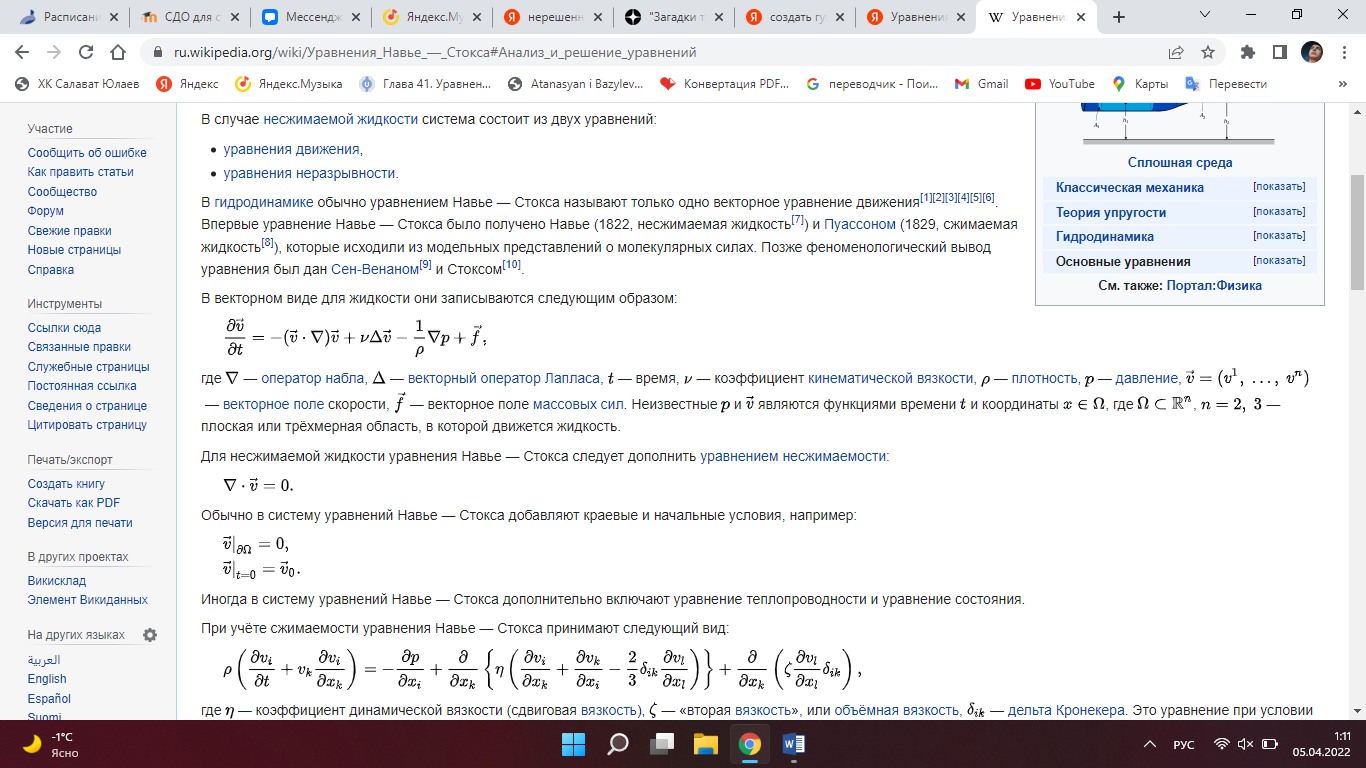 Проблема в том, что никто не знает ни их решения, ни каким образом их можно решить. Суть загадки состоит в том, чтобы доказать, что решение данных уравнений существует и что оно является гладкой функцией. 2. Гипотеза Римана (1859 год) Все мы учили в школе, что такое простые числа. Как известно, они делятся только на себя и на единицу. Например, 2, 3, 5, 7, 11 и т.д. Сколько их среди всех натуральных чисел - неизвестно, так как их распределение не поддается никакой закономерности. Немецкий математик Риман предположил, что можно выявить свойства, на основании которых сложилась последовательность простых чисел. Если это удастся сделать, нас ожидает значительный прогресс в сфере шифрования и безопасности сети Интернет. 3. Гипотеза Пуанкаре На сегодняшний день это единственная решенная задача тысячелетия. Она была сформулирована еще в 1904 году, и ее суть состояла в том, чтобы доказать, что поверхность сферы - односвязна, а поверхность тороида – нет. В классическом изложении эта задача выглядит так: если на яблоко (сфера) попытаться натянуть резиновую ленту, то посредством ее медленного перемещения и без отрыва от поверхности яблока, удастся сжать ее до точки. Если проделать эту же операцию с бубликом (тороид), сжать ленту до точки получится только если разорвать саму ленту или сломать бублик. В этом смысле предполагалось, что поверхность яблока является односвязной, а поверхность бублика - нет. Доказать это в 2002 году удалось российскому математику Григорию Яковлевичу Перельману. (Односвязное. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязна) 4. Гипотеза Ходжа (1941 год) В 20 веке математиками был открыт новый метод исследования формы сложных геометрических объектов, который и по сей день широко применяется на практике. Суть его такова: на основании свойств частей одного целого изучать свойства всего объекта. Гипотеза Ходжа как раз связана со свойствами как составных частей ("кирпичиков"), так и со свойствами целых объектов. На сегодняшний день в алгебраической геометрии это является достаточно серьезной проблемой: отыскать точные методы для анализа сложных предметов и форм на основании анализа его простых частей. 5. Уравнения Янга - Миллса (1954 год) Физики Янг и Миллс описывали мир элементарных частиц и обнаружили, что между геометрией и физикой элементарных частиц существует связь. Эти ученые написали уравнения, применимые в области квантовой физики, из которых следовало объединение теории электромагнитного, слабого и сильного взаимодействий. Таким образом, если на частицу оказывает воздействие сразу несколько полей, их суммарный эффект нельзя разложить на воздействие каждого из полей по отдельности. Происходит это от того, что, согласно теории, не только частицы материи притягиваются друг к другу, но также и силовые линии поля. На сегодняшний день уравнения Янга-Милса были приняты учеными-физиками во всем мире, однако предсказать массы элементарных частиц экспериментальным путем в рамках их теории так и не удалось. 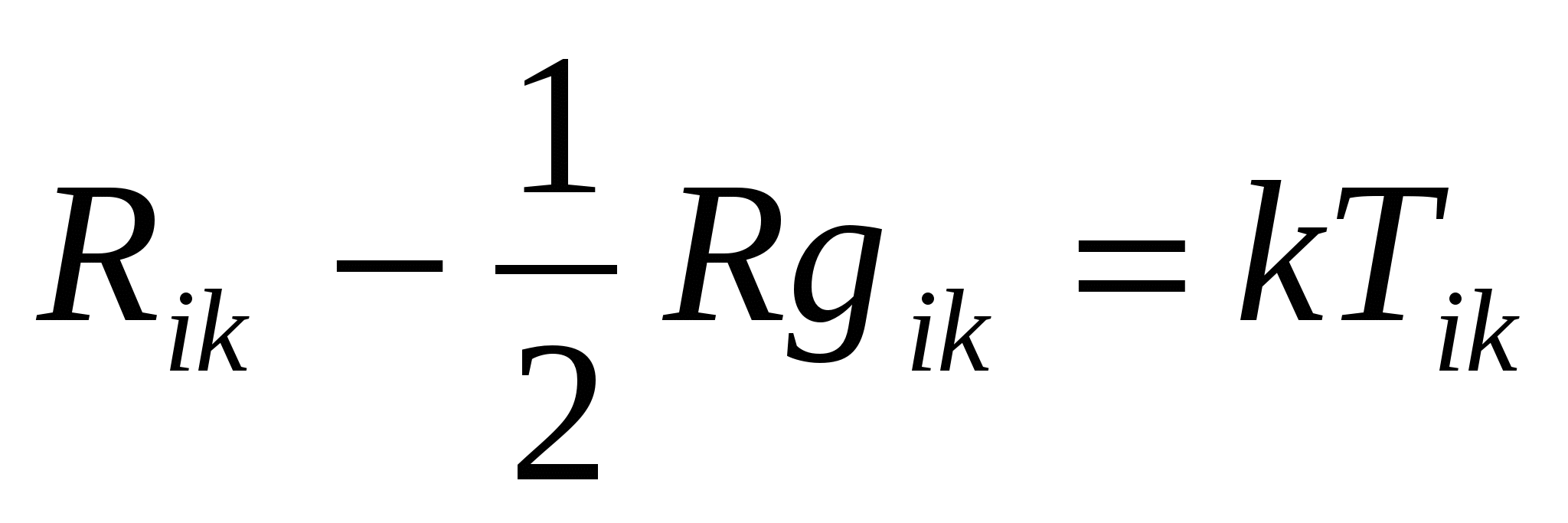 6. Гипотеза Бёрча и Свиннертон-Дайера (1960 год) Эта загадка связана с описанием алгебраических уравнений третьей степени (эллиптических кривых). Пример такого уравнения - x2 + y2 = z2. Полное описание решений этого выражения сделал еще Эвклид. Но найти решения в более сложных уравнениях на данный момент очень затруднительно. Суть задачи состоит в том, чтобы описать все возможные решения алгебраических уравнений с несколькими переменными, где х, у, z - целые числа. 7. Проблема Кука (1971 год) Эта задача также известна как "Равенство классов P и NP". Объясним ее на простом примере: Предположим, вы находитесь в большой компании и хотите найти своего знакомого. Если вам скажут, что он сидит где-то в углу - достаточно просто взглянуть и убедиться, так ли это. Но если вам не дали точного ответа касательно того, где конкретно находится нужный вам человек, вам придется потратить значительно больше времени, чтобы найти его среди остальных гостей. Итак вопрос: Возможно ли, что процесс проверки истинности решения какой-либо задачи будет продолжительнее, чем процесс решения этой самой задачи (независимо от алгоритма проверки)? |
