V011. Кинематика поступательного движения м т
 Скачать 0.86 Mb.
|
|
V031/V033. Импульс системы тел. Закон сохранения импульса. 1. Математическое выражение второго закона Ньютона в импульсной форме – 1)  2)  3)  4)  :3 2. Модуль импульса силы, действующей на горизонтальную плиту при упругом ударе о нее шарика массы m, движущегося вертикально вниз со скоростью V, равен 1)  2)  3)  4) 0:2 3. Приращение импульса шарика массы m, движущегося горизонтально со скоростью V, при упругом ударе о вертикальную стенку, равно 1) 2) 3) 4) 0:2 4. Теннисный мяч летел с импульсом  ( масштаб и направления указаны на рисунке). Теннисист произвел по мячу резкий удар со средней силой F = 80 Н. Изменившийся импульс мяча стал равным . Сила действовала на мяч в течение … с. 1) 0,5 2) 0,2 3) 2 4) 0,05 :4 5. [Импульс тела изменился под действием кратковременного удара и стал равным , как показано на рисунке. В момент удара сила действовала в направлении  1) 4 2) 1 3) 2 4) 3 :4 6. Тело массой m= 2 кг движется вдоль оси ОХ. Его движение описывается уравнением x=2+3t2t2, м. Проекция момента импульса на ось ОХ в момент времени t = 2c равна 1) 30 кг·м/с 2) – 1 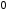 кг·м/с 3) 15 кг·м/с 4) – 5 кг·м/с :2 7. Тело брошено под углом к горизонту. За t = 5c полета модуль изменения импульса тела равен p = 200 кг·м/с. Сопротивление воздуха не учитывать. Масса этого тела равна … кг. Принять g равным 10 м/с2. 1) 2 2) 3 3) 4 4) 5 :3 8. ОШИБОЧНОЕ утверждение о замкнутой системе материальных точек – 1) импульс замкнутой системы материальных точек не изменяется с течением времени 2) механическая система называется замкнутой, если на нее не действуют внешние силы 3) в замкнутой системе сумма всех сил равна нулю 4) импульс замкнутой системы всегда равен нулю :4 9. Система взаимодействующих между собой точек является замкнутой. Для такой системы верными являются утверждения: 1) импульсы отдельных точек могут изменяться со временем 2) суммарный импульс системы может изменяться относительно инерциальной системы отсчета 3) система в целом (центр масс системы) может двигаться прямолинейно и равномерно относительно выбранной инерциальной системы отсчета 4) система в целом ( ее центр масс) может двигаться по криволинейной траектории относительно выбранной инерциальной системы отсчета1 :1,3 10. Система взаимодействующих между собой точек незамкнута, и равнодействующая внешних сил отлична от нуля. Для такой системы верными являются утверждения: 1) на систему действуют внешние силы 2) импульс системы сохраняется относительно выбранной инерциальной системы отсчета 3) импульс системы не сохраняется относительно выбранной инерциальной системы отсчета 4) векторная сумма всех сил, с которыми точки системы взаимодействуют между собой, равна нулю :1,3,4 11. Импульс силы, действующей на шарик массы m, движущийся вертикально вниз со скоростью V, при упругом ударе его о горизонтальную плиту, равен 1) 2) 3) 4) 0:2 1. Фигуристка, вращаясь вокруг вертикальной оси, раздвигает руки. При этом остается неизменным ее 1) модуль момента импульса 2) момент инерции 3) модуль угловой скорости 4) модули линейных скоростей различных точек тела :1 2. Человек, стоящий в центре вращающейся горизонтальной платформы в виде диска, переходит на ее край. При этом: 1) угловая скорость вращения платформы с человеком возрастет 2) угловая скорость вращения платформы с человеком уменьшится 3) угловая скорость вращения платформы с человеком не изменится 4) момент импульса платформы с человеком не изменится :2,4 3. Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест за его середину. Если он повернет шест из вертикального положения в горизонтальное, то частота вращения в конечном состоянии 1) уменьшится 2) не изменится 3) увеличится :1 4. Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках длинный шест, расположенный горизонтально, за его середину. Если он переместит шест вправо от себя, то частота вращения карусели в конечном состоянии 1) увеличится 2) не изменится 3) уменьшится :3 5. Человек, стоящий на краю горизонтальной, вращающейся платформы в виде диска перемещается ближе к центру платформы. Верными являются утверждения: 1) момент импульса платформы с человеком возрастает 2) момент импульса платформы с человеком не меняется 3) момент импульса платформы с человеком уменьшается 4) угловая скорость вращения платформы с человеком меняется :2,4 6. Формула, отражающая связь момента сил, действующих на тело, с моментом импульса этого тела – 1)  2)  3)  4) 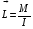 :2 7. На тело действует постоянный вращающий момент. Из перечисленных ниже характеристик вращательного движения по линейному закону изменяются следующие величины: 1) угол поворота 2) угловая скорость 3) угловое ускорение 4) момент импульса :2,4 8. Фигуристка, вращаясь вокруг вертикальной оси, начинает раздвигать руки. При этом уменьшается ее 1) модуль момента импульса 2) момент инерции 3) модуль угловой скорости 4) момент силы тяжести относительно вертикальной оси вращения :3 9. На тело, вращающееся вокруг неподвижной оси, в течение  действует вращающий момент M= 5 Нм. Момент импульса тела за это время изменится на … кгм2/с.:25 10. Материальная точка из состояния покоя движется под действием силы, изменяющейся по закону  . В момент времени  проекция импульса на ось ОХ равна … кгм/с.:20 V041/V043. Динамика вращательного движения. 1. . Момент инерции однородного тела зависит от: 1) момента приложенных к телу сил при заданной оси вращения 2) выбора оси вращения 3) формы тела 4) массы тела 5) углового ускорения :2,3,4 2. . Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО. Для моментов инерции относительно оси ОО справедливо соотношение  1) I1< I2 < I3 2) I1= I2 = I3 3) I1< I2 = I3 4)I1> I2 > I3 :1 3. Тонкостенная трубка и кольцо имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение  1) Iк = IТ 2) Iк > IТ 3) Iк < IТ :1 4. Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы. Массы шариков слева направо: 1 г, 2 г, 3 г, 4 г. Если поменять местами шарики 2 и 3, то то момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы  1) увеличится 2) не изменится 3) уменьшится :2 5. Момент импульса  твердого тела относительно оси вращения рассчитывается по формуле 1)  2) 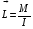 3)  4) :16. Направление момента силы, вызывающего вращение тела, совпадает с направлением вектора 1) силы 2) изменения момента импульса 3) момента импульса тела в начальный момент времени 4) момента импульса тела в конечный момент времени :2 7. Направление изменения момента импульса вращающегося тела всегда совпадает с направлением вектора 1) момента силы 2) угловой скорости 3) момента импульса тела в начальный момент времени 4) момента импульса тела в конечный момент времени :1 1. На рисунке приведена зависимость модуля моментов приложенных к телу сил от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером …  :1 2. Векторная форма основного закона динамики вращательного движения абсолютно твердого тела в импульсном виде – 1) 2)  3)  4) :2 2. Формула, отражающая связь момента сил, действующих на тело, с моментом импульса этого тела – 1) 2) 3) 4)  :2 3. На рисунке приведен график зависимости модуля результирующего момента сил, действующих на вращающееся твердое тело, от времени. Тело вращалось равномерно на интервале времени 1) от 0 до t1 2) от t1 до t2 3) от t2 до t3 4) от t3 до t4  :4 4. На рисунке приведен график зависимости модуля результирующего момента сил, действующих на вращающееся твердое тело, от времени. Тело вращалось с постоянным угловым ускорением на интервале времени 1) от 0 до t1 2) от t1 до t2 3) от t2 до t3 4) от t3 до t4 :2 5. На рисунках стрелками показаны направления вращения дисков и указано, как изменяется угловая скорость со временем. Вращающий момент сил, направленный вниз, приложен к дискам, приведенным под номерами: …  1) 1 и 2 2) 1 и 3 3) 1 и 4 4) 2 и 3 5) 2 и 4 6) 3 и 4 :4 6. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения.  Момент действующих на тело сил был постоянным и не равным нулю на участке … :2 7. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Момент импульса тела убывал на участках: … :4,5 8. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Максимальное по модулю угловое ускорение соответствует участку … :4 9. Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Массы шариков  и радиусы окружностей  указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика …  :4 10. На тело действует постоянный вращающий момент. Из ниже перечисленных характеристик вращательного движения в этом случае изменяется с течением времени пропорциональна квадрату времени следующая величина – 1) угол поворота 2) угловая скорость 3) угловое ускорение 4) момент импульса :1 11. На тело действует постоянный вращающий момент. Из перечисленных ниже величин изменяется со временем по линейному закону величина – 1) момент инерции 2) угловое ускорение 3) угловая скорость 4) кинетическая энергия вращения :3 12. Основное уравнение динамики вращательного движения – 1) 2) 3)  4) :1 13. Формула, выражающая второй закон Ньютона для вращательного движения – 1) 2) 3) 4) :3 14. На рисунке приведены различные виды графиков. Основному закону вращательного движения соответствует график….  :1 15. Верно указано направление момента силы для тела, совершающего равнозамедленное вращение, на рисунке …  :1 Дисциплина: Физика Тема: 060 Механические колебания и волны V061 – П Механические колебания S061 – П Механические колебания (незатухающие, затухающие, вынужденные 30 заданий) 1. [Уд1] (ВО1) Полная механическая энергия пружинного маятника увеличилась в 2 раза. При этом амплитуда колебаний … раз(а). 1) увеличилась в 2 2) увеличилась в 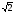 3) уменьшилась в 2 4) уменьшилась в 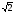:2 2. [Уд1] (ВО1) Материальная точка совершает гармонические колебания по закону 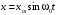 . График, на котором изображена зависимость проекции ускорения  этой точки от времени t – 1) 1  2) 2 3) 3 4) 4 :1 3. [Уд1] (ВО1) Материальная точка совершает колебания по закону  . График, на котором изображена зависимость кинетической энергии материальной точки от времени –  1) 1 2) 2 3) 3 4) 4 :2 4. [Уд1] (ВО1) Материальная точка совершает колебания по закону  . График, на котором изображена зависимость потенциальной энергии материальной точки от времени – 1) 1 2) 2 3) 3 4) 4 :4 5. [Уд1] (ВО1) На рисунке представлены графики гармонических колебаний материальных точек одинаковой массы, А1=2А2. Соотношение амплитудных значений ускорений колеблющихся точек следующее  1) am1 = am2 2) am1 < am2 3) am1 > am2 4) Однозначного ответа нет :2 6. [Уд1] (ВО1) На рисунке представлены графики гармонических колебаний материальных точек одинаковой массы, А1=2А2. Соотношение амплитудных значений скоростей колеблющихся точек следующее 1) Vm1 = Vm2 2) Vm1 < Vm2 3) Vm1 > Vm2 4) Однозначного ответа нет :1 7. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми коэффициентами упругости k. Маятник, имеющий наибольшую массу – … кг. 1)  2)  3)  4)  :4 8. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми коэффициентами упругости k. Маятник, имеющий наименьшую массу – … кг. 1) 2)  3)  4) :2 9. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми массами. Маятник, имеющий наибольший коэффициент упругости k – … Н/м. 1) 2) 3) 4) :2 10. [Уд1] (ВО1) Даны уравнения гармонических колебаний четырёх пружинных маятников с одинаковыми массами. Маятник, имеющий наименьший коэффициент упругости k – … Н/м. 1) 2) 3) 4) :4 11. [Уд1] (ВО1) Даны уравнения гармонических колебаний материальной точки массы m . Коэффициент упругости k наибольший в случае 1) х = 3 sin (2πt + π) м 2) х = 3 cos (4πt + 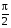 ) м 3) x= 5 cos (15πt – 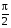) м 4) x= 5 sin (5πt) м :3 12. [Уд1] (ВО1) На рис.1 изображена зависимость проекции скорости материальной точки, совершающей гармонические колебания, от времени. На рис.2 график зависимости от времени проекции ускорения этой точки изображен под номером  1) 1 2) 2 3) 3 4) 4 :2 13. [Уд1] (ВО1) На рис.1 изображена зависимость проекции скорости материальной точки, совершающей гармонические колебания, от времени. На рис.2 график зависимости от времени смещения от положения равновесия этой точки изображен под номером  1) 1 2) 2 3) 3 4) 4 :1 14. [Уд1] (ВО1) Материальная точка массой m = 0,1 кг колеблется так, что проекция ах ускорения зависит от времени в соответствии с уравнением ах= 10 sin  , м/с2. Проекция силы на ось ОХ, действующей на материальную точку в момент времени t=  c равна … Н.1) 0,25 2) 0,5 3) 0,83 4) 1,0 : 2 15. [Уд1] (ВО1) Если в колебательной системе изменяющаяся физическая величина описывается законом  , то частота затухающих колебаний связана с собственной частотой соотношением 1)  2)  3)  4)  :4 16. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид  , где = 6 рад/с, = 8 с-1. Логарифмический декремент затухания колебаний равен 1) 83,7 2) 8,37 3) 0,63 4) 62,8 :2 17. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид , где = 6 рад/с, логарифмический декремент затухания = 8,37 . Коэффициент затухания колебаний равен … с-1.1) 8,0 2) 1,3 3) 0,6 4) 3,0 :1 18. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид  ,м. Если логарифмический декремент затухания колебаний λ = 0,1, то период T затухающих колебаний равен … мс.1) 20 2) 25 3) 40 4) 75 :2 19. [Уд1] (ВО1) Уравнение затухающих колебаний материальной точки имеет вид  ,м. Если логарифмический декремент затухания колебаний λ = 0,02, то частота ω затухающих колебаний равна … рад/с.1) 50 2) 100 3) 200 4) 300 :4 20. [Уд1] (ВО1) На рисунке изображен график затухающих колебаний, где х - колеблющаяся величина, описываемая уравнением х(t) = A0e-βtsin (ωt + φ). Коэффициент затухания β равен  1) 0,5 2) 1 3) 2 4) 2,7 :1 21. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии Wсистемы от времени. Обозначения вертикальных осей не указаны.  Зависимости кинетической энергии системы от времени в неконсервативной системе соответствует график 1) 1 2) 2 3) 3 4) 4 :2 22. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии Wсистемы от времени. Обозначения вертикальных осей не указаны. Зависимости полной энергии Wсистемы от времени в консервативной системе соответствует график 1) 1 2) 2 3) 3 4) 4 :1 23. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии Wсистемы от времени. Обозначения вертикальных осей не указаны. Зависимости смещения х от времени в консервативной системе соответствует график 1) 1 2) 2 3) 3 4) 4 :4 24. [Уд1] (ВО1) Приведены графики механических колебаний. Два графика соответствуют зависимости смещения х, два других – зависимости кинетической Wk и полной энергии Wсистемы от времени. Обозначения вертикальных осей не указаны. Зависимости смещения х от времени в неконсервативной системе соответствует график 1) 1 2) 2 3) 3 4) 4 :3 25. [Уд1] (ВО1) Приведены графики зависимости кинетической Wк и полной механической W энергии от времени t при различных видах механических колебаний. Обозначения осей ординат не указаны.  Зависимость полной энергии W от времени описывается … графиками. 1) 1 и 2 2) 2 и 4 3) 3 и 1 4) 4 и 3 :3 26. [Уд1] (ВО1) Уравнение движения пружинного маятника  является дифференциальным уравнением … колебаний.1) свободных незатухающих 2) затухающих 3) вынужденных 4) апериодических :2 27. [Уд1] (ВО1) Уравнение движения пружинного маятника  является дифференциальным уравнением … колебаний.1) свободных незатухающих 2) затухающих 3) вынужденных 4) апериодических :1 28. [Уд1] (ВО1) Уравнение движения пружинного маятника  является дифференциальным уравнением … колебаний.1) свободных незатухающих 2) затухающих 3) вынужденных 4) апериодических :3 29. [Уд1] (ВО1) Решение дифференциального уравнения  движения пружинного маятника ищется в виде зависимости 1) х = Acos (ω0t +o) 2) х = Aoe-tcos (ωt +o) 3) x = 2A cos 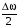 t cosωt 4) х = Ao e-2t cos (ω0t +o) :2 30. [Уд1] (ВО1) На рисунке представлена зависимость амплитуды колебаний груза на пружине с жесткостью k= 10 Н/м от частоты внешней силы. Максимальная энергия в этой системе равна … Дж. 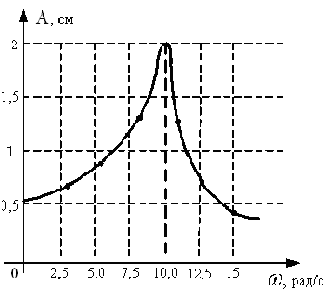 1) 0,002 2) 0,004 3) 20 4) 40 :1 C061 – П Механические колебания (сложение колебаний) – 16 заданий 1. [Уд1] (ВОМ) На рисунке под номерами 1, 2 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 3, 4 – векторные диаграммы сложения гармонических колебаний одного направления и одинаковой частоты (  - векторы амплитуд складываемых колебаний,  - вектор амплитуды результирующего колебания). Амплитуды складываемых колебаний равны для случаев, приведенных под номерами :1,3,4 2. [Уд1] (ВО1) Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями x= 3cost и y= -6cost. Траекторией результирующего движения точки является 1) прямая линия 2) парабола 3) окружность 4) эллипс :1 3. [Уд1] (ВО1) Складываются два гармонических колебания, происходящих в одном направлении. 1)  |