V011. Кинематика поступательного движения м т
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
, м и 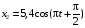 , м. , м.2)  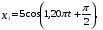 м и м и 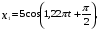 м. м.3) 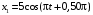 , м и , м и 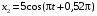 , м. , м. 4) 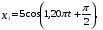 м и м и 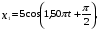 м. м.Результирующее движение называется биением в (во) … случае. 1) 1 2) 2 3) 3 4) 4 :2 4. [Уд1] (ВО1) Складываются два гармонических колебания, происходящих в одном направлении: 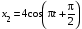 см и см и 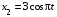 см. Амплитуда результирующего движения равна … см. см. Амплитуда результирующего движения равна … см.1) 7 2) 5 3) 3,5 4) 1 :2 5. [Уд1] (ВО1) Результат сложения двух гармонических колебаний одного направления с одинаковыми амплитудами и близкими частотами описывает уравнение 1) х = Acos (ω0t +o) 2) A2 = A12 +A22 + 2A1A2 cos 3) x = 2A cos 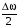 t cosωt t cosωt 4) 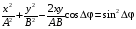 :3 6. [Уд1] (ВО1) Уравнение траектории при сложении двух гармонических колебаний взаимно перпендикулярных направлений с отличающимися амплитудами и одинаковыми частотами – 1) х = Acos (ω0t +o) 2) A2 = A12 +A22 + 2A1A2 cos 3) x = 2A cos 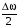 t cosωt t cosωt 4)  :4 7. [Уд1] (ВО1) Точка М одновременно совершает колебания по гармоническому закону вдоль осей координат ОХ и ОУ с одинаковыми амплитудами, разность фаз равна  . При соотношении частот 1:1 траектория точки имеет вид, соответствующий схеме под номером . При соотношении частот 1:1 траектория точки имеет вид, соответствующий схеме под номером  1) 1 2) 2 3) 3 4) 4 :3 8. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с различными амплитудами, но одинаковыми частотами. При разности фаз π траектория точки имеет вид, соответствующий схеме под номером  1) 1 2) 2 3) 3 4) 4 :2 9. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, и одинаковыми частотами. При разности фаз 0 траектория точки имеет вид, соответствующий схеме под номером  1) 1 2) 2 3) 3 4) 4 :4 10. [Уд1] (ВО1) Колебания точки М происходят вдоль осей Ох и Оу по закону синуса с одинаковыми амплитудами, но разными частотами. При разности фаз π/2 траектория точки имеет вид, соответствующий схеме под номером  1) 1 2) 2 3) 3 4) 4 :1 11. [Уд1] (ВО1) Точка М одновременно колеблется по гармоническому закону вдоль оcей координат ОХ и ОУ с одинаковыми амплитудами, разность фаз равна 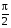 . При соотношении частот 3:2 траектория точки имеет вид на схеме, обозначенной номером . При соотношении частот 3:2 траектория точки имеет вид на схеме, обозначенной номером 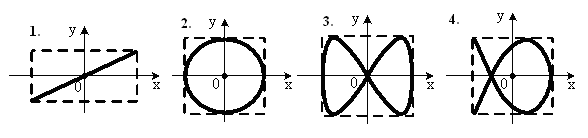 1) 1 2) 2 3) 3 4) 4 :4 12. [Уд1] (ВО1) При сложении двух взаимно-перпендикулярных колебаний одинаковой частоты траектория результирующего движения материальной точки представлена на рисунке. Тогда разность фаз складываемых колебаний равна 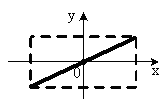 1) π 2) 0 3) 3π 4) π/2 :2 13. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1=4 см и А2=3 см. Амплитуда их результирующего колебания Ар=7 см. Разность фаз складываемых колебаний равна 1) ∆φ = 0 2) ∆φ = 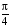 3) ∆φ = 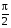 4) ∆φ = π :1 14. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар= 5 см. Разность фаз складываемых колебаний равна 1) ∆φ = 0 2) ∆φ = 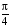 3) ∆φ = 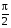 4) ∆φ = π :3 15. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Амплитуда их результирующего колебания Ар= 1 см. Разность фаз складываемых колебаний равна 1) ∆φ = 0 2) ∆φ = 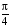 3) ∆φ = 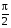 4) ∆φ = π :4 16. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Разность фаз складываемых колебаний равна ∆φ = 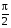 . Амплитуда их результирующего колебания составляет … см. . Амплитуда их результирующего колебания составляет … см.1) 7 2) 5 3) 1 4) 12 :2 Дисциплина: Физика Тема: 110 Физические основы молекулярной физики V114 – П Распределения Максвелла и Больцмана S114 – П Распределение Больцмана (3 задания) 1. [Уд1] (ВО1). На рисунке представлены зависимости давления от высоты для изотермической атмосферы, которые описываются барометрической формулой 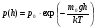 . Температуры связаны между собой соотношением . Температуры связаны между собой соотношением 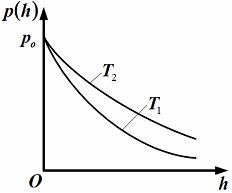 1) T1 = T2 2) T1 > T2 3) T1 < T2 :3 2. [Уд1] (ВО1). Воздух у поверхности Земли находится при нормальных условиях (100 кПа и 00 С) и его температура и ускорение свободного падения g = 9,8 м/с2 не зависит от высоты. Молярная масса равна M = 2910-3 кг/моль. Тогда отношение давления P1 воздуха на высоте 1 км к давлению P2 на дне скважины глубиной 1 км составляет 1) 0,5 2) 0,8 3) 1,2 4) 1,5 :2 3. [Уд1] (ВО1). Если температуру воздуха и ускорение силы тяжести считать не зависящими от высоты(t = 100 С, g = 9,8 м/с2, и M = 2910-3 кг/моль), то плотность воздуха в e раз (e - основание натурального логарифма) меньше по сравнению с его плотностью на уровне моря на высоте … км. 1) 8,3 2) 6,5 3) 1,2 4) 4,7 :1 C114 – П Распределение Максвелла – 13 заданий 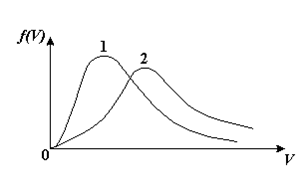 1. [Уд1] (ВОМ). Для распределения Максвелла по модулям скоростей молекул для разных газов при одинаковой температуре верны утверждения: 1) График 1 соответствует газу с большей массой молекул 2) График 2 соответствует газу с большей молярной массой. 3) Площадь под этими кривыми тем больше, чем больше молярная масса газа 4) Площади под этими кривыми одинаковы. :1,4 2. [Уд1] (ВОМ). Верные утверждения: 1) функция распределения Максвелла f(v) зависит от массы молекулы газа 2) функция распределения Максвелла f(v) не зависит от температуры 3) f(v) является величиной размерной 4) f(v) носит экстремальный характер :1,3,4 3. [Уд1] (ВО1). При изменении температуры Т газа средняя квадратичная скорость молекул этого газа увеличилась в 3 раза. Тогда максимальное значение функции распределения Максвелла 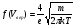 (e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а). (e - основание натурального логарифма, VB - наиболее вероятная скорость молекул) … раз(а).1) увеличится в 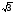 2) уменьшится в 9 3) уменьшится в 3 4) увеличится в 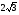 : 3 4. [Уд1] (ВОМ). Правильные утверждения о средней квадратичной скорости ( 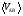 ) частиц системы, подчиняющейся распределению Максвелла: ) частиц системы, подчиняющейся распределению Максвелла:1) При одинаковой температуре 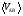 молекул различных идеальных газов одинакова. молекул различных идеальных газов одинакова.2) Средняя квадратичная скорость 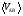 молекул газа при любой температуре меньше наиболее вероятной скорости. молекул газа при любой температуре меньше наиболее вероятной скорости.3) Чем больше масса молекулы газа, тем меньше 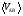 . .4) При возрастании температуры системы в четыре раза средняя квадратичная скорость 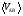 молекул увеличивается в два раза. молекул увеличивается в два раза.:3,4 5. [Уд1] (ВО1). Если средняя квадратичная скорость молекул водорода (M = 210-3 кг/моль) больше наиболее вероятной на V= 400 м/с, то температура газа равна … К. 1) 180 2) 381 3) 230 4) 450 :2 6. [Уд1] (ВО1). Если средняя квадратичная скорость молекул некоторого газа равна 500 м/с, то наиболее вероятная скорость составляет … м/с. 1) 327 2) 250 3) 630 4) 408 :4 7. [Уд1] (ВО1). Если при нагревании некоторого газа наиболее вероятная скорость молекул газа увеличилась в 2 раза, то средняя квадратичная скорость … раз(а). 1) увеличится в 4 2) уменьшится в 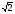 3) уменьшится в 8 4) увеличится в 2 :4 8. [Уд1] (ВО1). Если при нагревании некоторого газа средняя квадратичная скорость молекул газа увеличилась в 4 раза, при этом наиболее вероятная скорость … раз(а). 1) увеличится в 4 2) уменьшится в 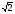 3) уменьшится в 8 4) увеличится в 2 :1 9. [Уд1] (ВО1). Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда значение f(Vвер) функции распределения Максвелла, соответствующее наиболее вероятной скорости молекул,.. 1)одинаково для всех газов 2) максимально для водорода 3) минимально для гелия 4) максимально для кислорода :4 10. [Уд1] (ВО1). Три газа: водород, гелий и кислород находятся при одинаковой температуре T. Тогда наиболее вероятная скорость Vвер… 1) у всех газов одинакова 2) у кислорода наибольшая 3) у гелия наименьшая 4) у водорода наибольшая : 4 11. [Уд1] (ВО1). В статистике Максвелла функция распределения имеет вид 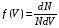 . НЕВЕРНОЕ утверждение о функции Максвелла – . НЕВЕРНОЕ утверждение о функции Максвелла – 1) f(V) - вероятность того, что скорость данной молекулы находится в единичном интервале скоростей вблизи заданной скорости V. 2) f(V)dV- вероятность того, что скорость данной молекулы заключена в интервале скоростей от V до V+dV. 3) f(V) - относительное число молекул, скорости которых заключены в интервале скоростей от V до V+dV. 4) f(V)NdV - абсолютное число молекул, скорости которых заключены в интервале скоростей от V до V+dV. :4 или 3?????? 12. [Уд1] (ВОМ). Правильные утверждения о наиболее вероятной скорости Vвер частиц системы, подчиняющейся распределению Максвелла: 1) Наиболее вероятная скорость Vвер зависит от температуры и молярной массы идеального газа. 2) Скорость Vвер можно найти, приравняв нулю производную функции распределения Максвелла по скоростям: 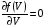 . .3) Чем больше молярная масса газа, тем меньше при данной температуре значение Vвер. 4) Vвер линейно возрастает с увеличением температуры. :1,2,3 13. [Уд1] (ВО1). На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 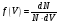 - доля молекул, скорости которых заключены в интервале от - доля молекул, скорости которых заключены в интервале от 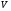 до до 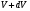 в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с большеймолярной массой и таким же числом молекул, то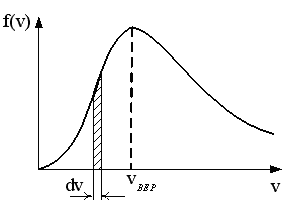 1) величина максимума уменьшится 2) площадь под кривой увеличится 3) максимум кривой сместится влево, в сторону меньших скоростей 4) максимум кривой сместится вправо, в сторону больших скоростей :3 S115 – М Распределение Больцмана -5 заданий 1. [Уд1] (ВОМ). Распределение Больцмана характеризует: 1) равновесное распределение частиц по координатам в стационарном потенциальном поле. 2) системы, состоящие как электронейтральных, так и заряженных классических частиц. 3) системы частиц со скоростями близкими к скорости света. :1,2 2. [Уд1] (ВОМ). Формула 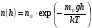 описывает распределение одинаковых молекул массой описывает распределение одинаковых молекул массой 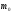 по высоте в изотермической атмосфере; здесь по высоте в изотермической атмосфере; здесь 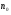 – концентрация молекул при – концентрация молекул при 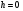 , n – их концентрация на высоте h. Для этой зависимости справедливы следующие утверждения: , n – их концентрация на высоте h. Для этой зависимости справедливы следующие утверждения:1) приведенные на рисунке кривые соответствуют распределениям для одного и того же газа при T2 > T1 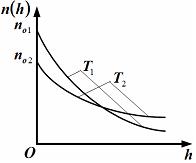 2) приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем m1 > m2 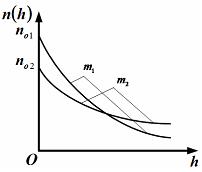 3) приведенные на рисунке кривые соответствуют распределениям для одного и того же газа, причем T2 < T1 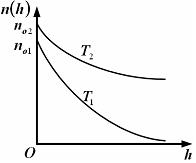 4) приведенные на рисунке кривые соответствуют распределениям для двух разных газов при одинаковой температуре, причем массы молекул удовлетворяют соотношению m1 < m2  :1,2 3. [Уд1] (ВО1). Отношение концентрации 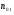 молекул водорода (M1 = 210-3 кг/моль) к концентрации молекул водорода (M1 = 210-3 кг/моль) к концентрации 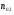 молекул азота (M2 = 2810-3 кг/моль) равно 0, а на высоте h соответствующее составляет h. Если температура Т = 380 Ки ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, а отношение составляет молекул азота (M2 = 2810-3 кг/моль) равно 0, а на высоте h соответствующее составляет h. Если температура Т = 380 Ки ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, а отношение составляет 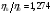 , то высота h равна … км. , то высота h равна … км.1) 3 2) 6 3) 4,5 4) 8,7 :1 4. [Уд1] (ВО1). Отношение концентрации 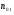 молекул водорода (M1 = 210-3 кг/моль) к концентрации молекул водорода (M1 = 210-3 кг/моль) к концентрации 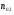 молекул азота (M2 = 2810-3 кг/моль) равно 0, а на высоте h = 3000 м соответствующее составляет h. Если температура Т и ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, а отношение составляет молекул азота (M2 = 2810-3 кг/моль) равно 0, а на высоте h = 3000 м соответствующее составляет h. Если температура Т и ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, а отношение составляет 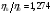 , то температура равна … К. , то температура равна … К.1) 380 2) 250 3) 540 4) 410 :1 5. [Уд1] (ВО1). Плотность водорода h на высоте h на 10% меньше его плотности 0 на уровне моря. Если температура Т = 273 Ки ускорение свободного падения g = 9,8 м/с2 не зависят от высоты, то высота h равна … км. 1) 6,8 2) 9,4 3) 12,2 4) 15,7 :3 C115 – М Распределение Максвелла – 13 заданий 1. [Уд1] (ВО1). Функция распределения Максвелла для молекул газа имеет вид 1) 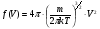 2) 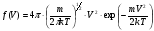 3) 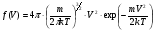 4) 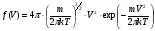 :3 2. [Уд1] (ВО1). Если давление и плотность молекул газа соответственно составляют Р = 40 кПа и = 0,35 кг/м3, то наиболее вероятная скорость равна … м/с. 1) 478 2) 630 3) 250 4) 346 :1 3. [Уд1] (ВО1). Если плотность газа = 0,35 кг/м3, наиболее вероятная скорость его молекул 630 м/с, то давление равно … кПа. 1) 23,4 2) 69,5 3) 47,8 4) 53,6 :2 4. [Уд1] (ВО1). При нагревании некоторого газа средняя арифметическая скорость молекул этого газа увеличилась в 2 раза. При этом наиболее вероятная скорость … раз(а). 1) увеличилась в 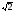 2) увеличилась в 4 3) уменьшилась в 8 4) увеличилась в 2 :4 5. [Уд1] (ВО1). В сосуде находятся одинаковые количества азота N2 и водорода H2. Распределение скоростей молекул газа в сосуде будет описываться кривыми, изображенными на рисунке под номером 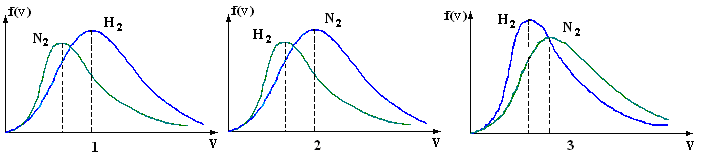 1) 1 2) 2 3) 3 4) правильного рисунка нет :4 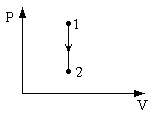 6. [Уд1] (ВО1). На (Р,V) – диаграмме показан процесс, производимый идеальным газом в изолированной сосуде. Начальное и конечное состояния будут соответствовать распределениям скоростей, изображенным на рисунке 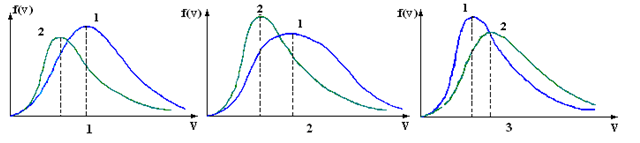 1) 1 2) 2 3) 3 :2 7. [Уд1] (ВО1). В трех одинаковых сосудах находится одинаковое количество газа при разных температурах. Распределение скоростей молекул в сосуде с максимальной температурой будет описывать кривая, обозначенная номером 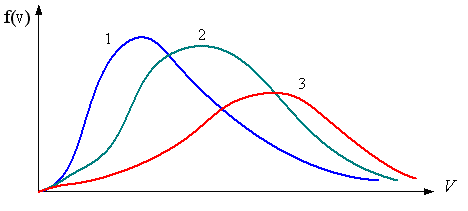 1) 1 2) 2 3) 3 :3 8. [Уд1] (ВО1). Максимальное значение функции распределения Максвелла при данной температуре Т равно 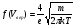 (e - основание натурального логарифма, VB - наиболее вероятная скорость). Если при изменении температуры газа f(VB) уменьшится в 2 раза, то средняя квадратичная скорость молекул газа … раза. (e - основание натурального логарифма, VB - наиболее вероятная скорость). Если при изменении температуры газа f(VB) уменьшится в 2 раза, то средняя квадратичная скорость молекул газа … раза.1) увеличится в 4 2) уменьшится в 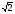 3) уменьшится в 2 4) увеличится в 2 :4 9. [Уд1] (ВОМ). Правильные утверждения, относящиеся к функциям распределения Максвелла и Больцмана: 1) Функция распределения Максвелла позволяет найти распределение молекул по значениям потенциальной энергии. 2) Распределение Больцмана справедливо только в потенциальном поле силы тяжести. 3) Распределение молекул в пространстве устанавливается в результате совместного действия теплового движения и потенциального поля. 4) Распределение Больцмана характеризует распределение частиц классической системы по координатам после установления в системе равновесия. :3,4 10. [Уд1] (ВО1). Если молярные массы азота и кислорода соответственно равны M1= 2810-3 кг/мольи M2= 3210-3 кг/моль, а наиболее вероятные скорости молекул азота и кислорода будут отличаться друг от друга на V = 30 м/c, то температура смеси газов равна … К. 1) 180 2) 256 3) 363 4) 450 :3 11. [Уд1] (ВО1). При некоторой температуре распределение молекул газа по модулям скоростей оказалось таким, что скоростям V1 = 200 м/с и V2 = 800 м/с соответствует одинаковое значение функции распределения Максвелла f(v). Тогда наиболее вероятная скорость молекул этого газа равна … м/с. 1) 250 2) 346 3) 465 4) 630 :3 12. [Уд1] (ВО1). При скорости V1= 800 м/с значения функции распределения Максвелла по модулям скоростей f(V) одинаковы для кислорода и азота (см. рисунок). Молярные массы газов равны, соответственно, M1 = 3210-3 кг/моль и M2 = 2810-3 кг/моль. Тогда смесь газов находится при температуре … К. 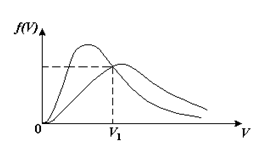 1) 258 2) 471 3) 650 4) 769 :4 13. [Уд1] (ВО1). На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 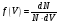 - доля молекул, скорости которых заключены в интервале от - доля молекул, скорости которых заключены в интервале от 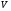 до до 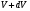 в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с меньшеймолярной массой и таким же числом молекул, то в расчете на единицу этого интервала. Если, не меняя температуры, взять другой газ с меньшеймолярной массой и таким же числом молекул, то 1) высота максимума увеличится 2) площадь под кривой уменьшится 3) максимум кривой сместится вправо, в сторону больших скоростей 4) максимум кривой сместится влево, в сторону меньших скоростей :4 S116 – МУО+КЗ Распределение Больцмана – 4 задания 1. [Уд1] (ВО1). Распределение Больцмана описывает распределение частиц по 1) координатам 2) кинетическим энергиям 3) импульсам 4) скоростям :1 2. [Уд1] (ВОМ). Распределение Больцмана можно использовать, если справедливы утверждения: 1) температура в разных частях системы одинакова 2) температура в разных частях системы неодинакова 3) импульсы всех молекул системы одинаковы 4) система находится в состоянии равновесия :1,4 3. [Уд1] (ВО1). Установленная вертикально закрытая с обоих концов труба наполнена газообразным кислородом M = 3210-3 кг/моль. Высота трубы h = 200 м, ускорение силы тяжести g = 9,8 м/с2. Стенки трубы имеют всюду одинаковую температуру Т = 293 К. Давление газа внутри трубы вблизи ее основания равно Р0 = 105 Па. Давление Рh в трубе вблизи верхнего его конца равно … кПа. 1) 87 2) 110 3) 97 4) 100 :3 4. [Уд1] (ВО1). На взлетной площадке барометр показывает давление P0 = 100 кПа, а в кабине вертолета барометр показывает давление P = 90 кПа. Если температура воздуха (Т = 293 К) и ускорение силы тяжести (g = 9,8 м/с2) не изменяются с высотой и, молярная масса воздуха равна M = 2910-3 кг/моль, то высота h, на которой летит вертолет, равна … м. 1) 800 2) 900 3) 1000 4) 750 :2 C116 – МУО+КЗ Распределение Максвелла – 4 задания 1. [Уд1] (ВОМ) Абсолютное число dN молекул идеального газа, скорости которых при данной температуре T заключены в интервале от V до V + dV, зависит от: 1) температуры газа 2) от общего числа N молекул этого газа 3) от объема, занимаемого газом 4) от значения скорости V, в окрестности которой выбран рассматриваемый интервал dV :1,2,4 2. Абсолютное число dN молекул идеального газа, скорости которых при данной температуре T заключены в интервале от V до V + dV, НЕ зависит от: 1) температуры газа 2) общего числа N молекул этого газа 3) объема, занимаемого газом 4) значения скорости V, в окрестности которой выбран рассматриваемый интервал dV :3 2. [Уд1] (ВО1). Функция распределения Максвелла 1) не имеет экстремальный вид 2) является величиной безразмерной 3) может быть величиной отрицательной 4) при заданной температуре может соответствовать двум различным скоростям молекул газа :4 3. [Уд1] (ВОМ). В статистике Максвелла функция распределения имеет вид 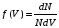 . Верные утверждения: . Верные утверждения:1) f(V) - относительное число молекул, скорости которых лежат в единичном интервале скоростей вблизи заданного значения скорости V. 2) f(V)dV - относительное число молекул, скорости которых заключены в интервале скоростей от V до V+dV. 3) f(V)NdV - число молекул, скорости которых заключены в интервале скоростей отV до V+dV. 4) 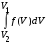 - абсолютное число молекул, скорости которых заключены в интервале от скорости V1 до скорости V2. - абсолютное число молекул, скорости которых заключены в интервале от скорости V1 до скорости V2.:1,2,3 4. [Уд1] (ВОМ). На рисунке изображен график функции распределения Максвелла молекул идеального газа по модулю скоростей. Тогда площадь заштрихованной полоски есть: 1) относительное число молекул 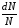 , скорости которых заключены в интервале от V до V + dV. , скорости которых заключены в интервале от V до V + dV.2) вероятность того, что скорость данной молекулы имеет значение, заключенное в интервале от V до V + dV. 3) доля молекул, скорости которых заключены в интервале от V до V + dV.  4) число частиц, скорости которых заключены в интервале от V до V + dV. :1,2,3 |
