Моделирование социально-экономических процессов. Вариант 1 Какие задачи линейного программирования называются транспортными

• Название: Вариант 1 Какие задачи линейного программирования называются транспортными
• Дата: 29.04.2023
• Размер: 136 Kb.
• Имя файла: Моделирование социально-экономических процессов.doc
• Тип: Задача; #1096967

Практическое задание 2

Задания: Определить оптимальный план перевозок с минимальными затратами для исходных данных, приведенных ниже.

Вариант 1
Какие задачи линейного программирования называются транспортными?

Транспортная задача (ТЗ) является важнейшей частной задачей линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта. Она выделяется в линейном программировании определённостью экономической характеристики, особенностями математической модели, наличием специфических методов решения.

К ЗЛП транспортного типа приходят при рассмотрении различных практических ситуаций, связанных с составлением наиболее экономичного плана перевозок продукции, управления запасами, назначением персонала на рабочие места, оборотом наличного капитала и многими другими.

На транспорте наиболее часто встречаются следующие задачи, относящиеся к транспортным:

- прикрепление потребителей ресурса к производителям;

- привязка пунктов отправления к пунктам назначения;

- взаимная привязка грузопотоков прямого и обратного направлений;

- отдельные задачи оптимальной загрузки промышленного оборудования;

- оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.

Каковы особенности математической модели транспортной задачи?

Особенности экономико-математической модели транспортной задачи:

• система ограничений есть система уравнений (т.е. транспортная задача задана в канонической форме);

• коэффициенты при переменных системы ограничений равны единице или нулю;

• каждая переменная входит в систему ограничений два раза.

Для математической формулировки транспортной задачи в общей постановке обозначим через cij коэффициенты затрат, через Мi — мощности поставщиков, через Nj — мощности потребителей, где
i= 1, 2, ..., m; j = 1, 2, ..., n; m — число поставщиков, n — число потребителей.

Какие транспортные задачи называются открытыми и закрытыми?

Начнем с определения транспортной задачи. Условно говоря, у вас есть товар, расположенный на нескольких складах. Необходимо доставить товар нескольким потребителям – это могут быть магазины, ларьки на рынке и т.д. – при этом у вас есть выбор из нескольких маршрутов. Каждый потребитель имеет свою потребность в товаре, кому-то нужно получить, к примеру, 10 тонн груза, а кому-то хватит и 5 тонн товара.

Ясно, что стоимость перевозки будет различаться в зависимости от количества перевозимого груза и дальности пути. Минимизировать нужно суммарные затраты на перевозку груза. Введем нужные обозначения, пусть n

– количество складов, а m – количество точек назначения (потребителей). Через С(i,j)=cij обозначим стоимость перевозки одной единицы груза из i-го склада к j

-му потребителю.

При этом a(i)=ai

означает запас груза у i-го склада, а b(j)=bj – потребность соответствующего потребителя. Ясно, что общая стоимость перевозки вычисляется как сумма всех затрат на перевозку товара от каждого склада к каждому потребителю. Пусть вас не пугает такая общая постановка задачи, если из какого-то склада нельзя перевезти товар, например из-за невыгодного расположения, то соответствующий b

можно установить равным нулю.

Теперь можно перейти к математической формулировке задачи. На языке формул задача примет следующий вид:

∑i=1m∑j=1ncijxij→min

при следующих ограничениях:

∑nj=1xij=ai,∑mi=1xij=bj,xij≥0,cij≥0,ai≥0,bj≥0,i=1,2,...,m;j=1,2,...,n.

В такой постановке все ясно и дальнейших пояснений не требуется. Остается только решить транспортную задачу.

Существует две разновидности транспортной задачи – открытая и закрытая. Закрытая задача характеризуется тем, что суммарная потребность всех потребителей равна суммарным запасам всех складов. То есть, весь товар на всех складах будет реализован полностью. Математически это пишется как

∑i=1mai=∑j=1nbj.

В открытой задаче суммарная потребность и суммарные запасы не совпадают. Например, какой-то склад не реализуется товар полностью, появляются остатки продукции. В этом случае процесс решения транспортной задачи немного усложняется, потребуется ввести фиктивного поставщика или потребителя с нулевыми стоимостями перевозки.

Могут ли объемы перевозок быть отрицательными?

объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения, так как модель сбалансирована, то вся продукция должна быть вывезена от производителя, а потребности всех центров распределения должны быть полностью удовлетворены.

В чем особенность целевой функции транспортной задачи?

Целевая функция выражается линейной формой. Матрица целевой функции — это матрица-строка, элементами которой могут быть расстояния, время или стоимость перевозки.

Ввиду особенностей математической формы и постановки транспортной задачи линейного программирования « для решения ее разработаны специальные методы, позволяющие из бесчисленного множества возможных решений найти оптимальное. Одним из таких методов является распределительный, имеющий несколько разновидностей, которые отличаются в основном способом выявления оптимального решения.

Практическое задание 1
Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам.

Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Важным и нетривиальным этапом построения регрессионной модели является выбор уравнения регрессии. Этот выбор основывается на теоретических данных об изучаемом явлении и предварительном анализе имеющихся статистических данных.

Уравнение парной линейной регрессии имеет вид:

,

где - теоретические значения результативного признака, полученные по уравнению регрессии; - коэффициенты (параметры) уравнения регрессии.

Модель регрессии строится на основании статистических данных, причем могут использоваться как индивидуальные значения признака, так и сгруппированные данные. Для выявления связи между признаками по достаточно большому числу наблюдений статистические данные предварительно группируют по обоим признакам и строят корреляционную таблицу. При помощи корреляционной таблицы отображается только парная корреляционная связь, т.е. связь результативного признака с одним фактором. Оценка параметров уравнения регрессии осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и требование минимальности суммы квадратов отклонений эмпирических данных от выровненных значений результативного фактора :
.

Для линейного уравнения регрессии имеем:



Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений: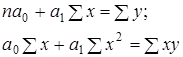



где - объем исследуемой совокупности (число единиц наблюдения).

Решение системы нормальных уравнений позволяет найти параметры уравнения регрессии .

Коэффициент парной линейной регрессии является средним значением в точке , поэтому его экономическая интерпретация затруднена. Смысл этого коэффициента можно трактовать как усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов. Коэффициент показывает, на сколько в среднем изменяется значение результативного признака при изменении факторного признака на единицу.

После получения уравнения регрессии необходимо проверить его адекватность, то есть соответствие фактическим статистическим данным. С этой целью производится проверка значимости коэффициентов регрессии: выясняется, насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом случайного стечения обстоятельств.


В чем суть метода наименьших квадратов?

Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

Приведите примеры нелинейных моделей по объясняющей переменной x.

Хотя во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат, однако ограничиться рассмотрением лишь линейных регрессионных моделей невозможно. Так, близость линейного коэффициента корреляции к нулю еще не значит, что связь между соответствующими экономическими переменными отсутствует. При слабой линейной связи может быть очень тесной, например, не линейная связь. Поэтому необходимо рассмотреть и нелинейные регрессии, построение и анализ которых имеют свою специфику.

В случае, когда между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных эконометрических моделей.

Различают две группы нелинейных регрессионных моделей:

­- модели, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

­ - модели нелинейные по оцениваемым параметрам.

К первой группе относятся, например, следующие виды функций:
- полином 2-й степени;

- полином 3-й степени;

- гипербола.

Ко второй группе относятся:

- степенная;

- показательная;

- экспоненциальная и др. виды функций.

Классическим примером функций, относящихся к первой группе, являются кривые Филипса и Энгеля:

и , соответственно.

Первая функция характеризует нелинейные соотношения между нормой безработицы x и процентом прироста заработной платы у. Из данной зависимости следует, что с ростом уровня безработицы темпы роста заработной платы в пределе стремится к нулю.

Вторая функция устанавливает закономерность – с ростом дохода доля расходов на продовольствие - уменьшается. Здесь у, обозначает - долю расходов на непродовольственные товары; х – доходы.

Первая группа нелинейных функций легко может быть линеаризована (приведены к линейному виду). Например, для полинома к-го порядка

производя замену:

, , ,…,

получим линейную модель вида

.

Аналогично могут быть линеаризованы и другие виды нелинейных функций 1-й группы, производя соответствующие замены.

Для оценки параметров нелинейных функций первой группы можно использовать, обычный МНК, аналогично, как и в случае линейных функций.

Иначе обстоит дело с группой регрессионных, нелинейных функций по оцениваемым параметрам. Данную группу функций можно разбить на две подгруппы: ­нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные.
Рассмотрим степенную функцию . Она нелинейна относительно параметров и b. Однако ее можно считать внутренне линейной, так как, прологарифмировав ее можно привести к линейному виду:

.

Следовательно, ее параметры могут быть найдены обычным МНК.

Если модель представить в виде:

, то модель становится внутренне нелинейной, т.к. ее невозможно преобразовать в линейный вид.

Внутренне нелинейной будет и модель вида



В эконометрических исследованиях, часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые легко преобразуются в линейный вид, относятся к группе линейных моделей. Например, к линейным относят модель:

, так как

.

Если, модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные методы, успешность которых зависит от вида функции и особенностей применяемого итеративного подхода.

МНК в случае нелинейных функций, рассмотрим на примере оценки параметров степенной функции .

Прологарифмировав данную функцию, получим:

или, производя обозначения:

, где

; ; ; .

Применив МНК к полученному уравнению: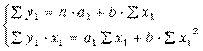

, или



Параметр b определяется непосредственно из системы, а параметр а – косвенным путем:

Оценка корреляции для нелинейной регрессии

Оценка тесноты корреляционной зависимости в случае нелинейной регрессии производится с помощью индекса корреляции (R):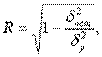



где , , ,

значения результативного признака, рассчитанные по уравнению регрессии.

Величина данного показателя находится в границах: , чем она ближе к единице, тем теснее связь рассматриваемых признаков, тем надежнее найденное уравнение регрессии.

Следует помнить, что если для линейной зависимости имеет место равенство: , то при криволинейной зависимости не равен .Величина R² называется индексом детерминации.

Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера: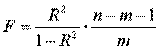

,

где R² - индекс детерминации;

n - число наблюдений;

m - число параметров при переменных х.

Индекс детерминации можно сравнивать с коэффициентом детерминации для обоснования возможности применения линейной функции.

Если величина 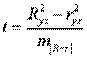не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия между и r²_yx, вычисленных по одним и тем же исходным данным, через t - критерий Стьюдента:

,

где ,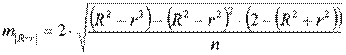

Если , то различия между и существенны и замена нелинейной регрессии линейной - невозможна. Практически, если , то различия между и несущественны, и, следовательно, возможно применение линейной регрессии.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. 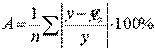и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Чтобы иметь общее представление о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:



Существует и другая формула определения средней ошибки аппроксимации: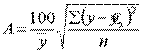

, где .

Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.

Возможность построения нелинейных моделей, как с помощью их приведения к линейному виду, так и путем использования нелинейной регрессии, значительно повышает универсальность регрессионного анализа, но и усложняет задачу исследователя.

Возникает вопрос: с чего начать - с линейной зависимости или с нелинейной, и если с последней, то, какого типа.

Если ограничиться парной регрессией, то можно построить график наблюдений у и х и принять решение. Однако очень часто несколько разных нелинейных функций приблизительно соответствуют наблюдениям, если они лежат на некоторой кривой. А в случае множественной регрессии невозможно даже построить график.

При рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной процедура выбора достаточно проста. Наиболее разумным является оценивание регрессии на основе всех вероятных функций, и выбор функции, в наибольшей степени объясняющей изменения зависимой переменной. Если для одной модели коэффициент R² значительно больше, чем для другой, то вы сможете сделать оправданный выбор без особых раздумий, однако, если значения R² для двух моделей приблизительно равны, то проблема выбора существенно усложняется.

В этом случае следует использовать стандартную процедуру, известную под названием теста Бокса – Кокса.

Если необходимо сравнить модели с использованием у и lny в качестве зависимой переменной, то можно использовать вариант теста, разработанный Полом Зарембкой. Процедура включает следующие шаги:

1) Вычисляется среднее геометрическое значений у в выборке, (оно совпадает с экспонентой среднего арифметического lny):



2) Пересчитываются наблюдения у, т.е. они делятся на это значение, то есть



3) Оценивается регрессия для линейной модели с использованием у^*_i вместе y_i и для логарифмической модели с использованием ln(y^*_i) вместо ln(y_i). Теперь значения суммы квадратов отклонений для двух регрессий сравнимы, и, следовательно, модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие.