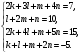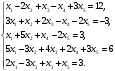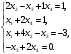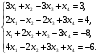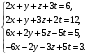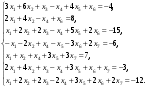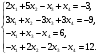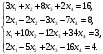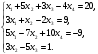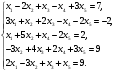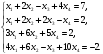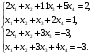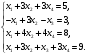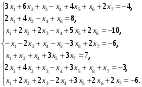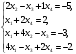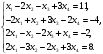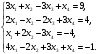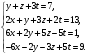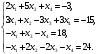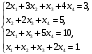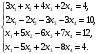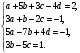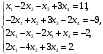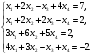лабораторная матлаб. Отчет. Вариант 1 Параметры векторов и матриц
 Скачать 456.79 Kb. Скачать 456.79 Kb.
|
|
Вариант 1 1. Параметры векторов и матриц Задаться вектором V и матрицей M. 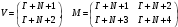 - чётные варианты - чётные варианты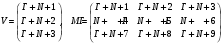 - нечётные варианты - нечётные вариантыГ – последняя цифра текущего года, N – номер обучающегося в списке группы. Г и N не закладывать как переменные. Взять конкретные значения для каждой из позиции (допустимо объединить значения знаками операций, допустимо так же записывать заранее вычисленный результат).  %Задаем Матрицы V=[2020+1+1;2020+1+2;2020+1+3]; M=[2020+1+1 2020+1+2 2020+1+3; 2020+1+4 2020+1+5 2020+1+5; 2020+1+7 2020+1+8 2020+1+9]; Г=2020; N=1 Листинг в Matlab Для вектора и матрицы применить следующие функции: disp(V); 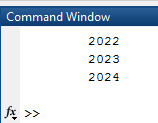 Выводится вектор V disp(V(1)); 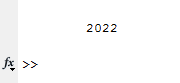 Выводится 1 элемент вектора V length(V); 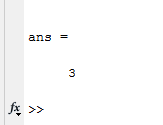 Выводится длина вектора V size(V); 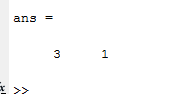 Выводится размерность вектора V как матрицы (3 строки и 1 столбец) disp(M); 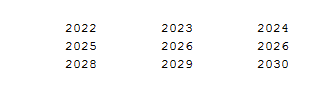 Выводится матрица М disp(M(1)); Выводится первый элемент матрицы М disp(M(1,1)); 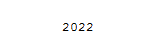 Выводится элемент строки 1 и столбца 1 матрицы М length(M); 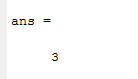 Выводится длина матрицы М как вектора size(M). 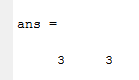 Выводится размерность матрица М как матрицы 2. Работа с переменными в матрице 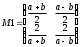 - чётные варианты - чётные варианты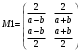 - нечётные варианты - нечётные вариантыГде a = Г * N, b = Г + N, Г – последняя цифра текущего года, N – номер варианта обучающегося в списке группы. Вывести каждое значение в матрице через соответствующие индексы элементов. Листинг в Matlab  clc; a=2020*1; b=2020+1; M1=[2./(a-b) 2./(a+b); (a-b)./2 (a+b)./2]; disp('Элемент 1,1'); disp(M1(1,1)); disp('Элемент 1,2'); disp(M1(1,2)); disp('Элемент 2,1'); disp(M1(2,1)); disp('Элемент 2,2'); disp(M1(2,2)); Результат 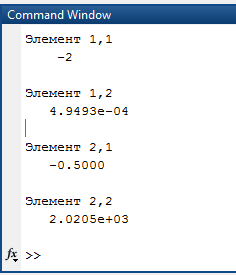 3. Работа с матрицей через индексацию Заполнить матрицу M2 теми же элементами, что содержатся в M и в том же порядке, но заполнение значениями матрицы выполнить через соответствующие индексы. Например, 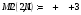 . . Листинг в Matlab  clc; a=2020*1; b=2020+1; M1=[2./(a-b) 2./(a+b); (a-b)./2 (a+b)./2]; M2(1,1)=M1(1,1); M2(1,2)=M1(1,2); M2(2,1)=M1(2,1); M2(2,2)=M1(2,2); 4. Обособление столбца матрицы Создать вектор 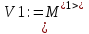 - (первый столбец M) нечётные варианты, - (первый столбец M) нечётные варианты, 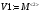 - (второй столбец M) чётные варианты. - (второй столбец M) чётные варианты.Прокомментировать какими именно элементами из M он заполнился. Создать вектор 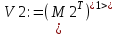 - (первый столбец из транспонированной M2) нечётные варианты, - (первый столбец из транспонированной M2) нечётные варианты, 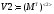 - (второй столбец из транспонированной M2) чётные варианты. - (второй столбец из транспонированной M2) чётные варианты. Прокомментировать, какими именно элементами из М или М2 он заполнился. Вывести на лист содержимое 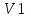 и и 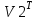 для нечётных вариантов; для нечётных вариантов; 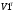 и и 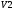 - для чётных вариантов. - для чётных вариантов.Листинг в Matlab  clc; a=2020*1; b=2020+1; M1=[2./(a-b) 2./(a+b); (a-b)./2 (a+b)./2]; disp('Элемент 1,1'); disp(M1(1,1)); disp('Элемент 1,2'); disp(M1(1,2)); disp('Элемент 2,1'); disp(M1(2,1)); disp('Элемент 2,2'); disp(M1(2,2)); Результат 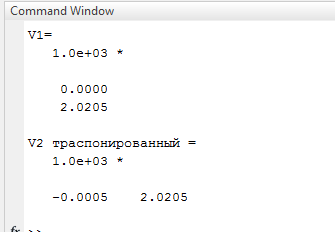 Вектор V1 заполнился элементами 2 столбца матрицы, вектор V2 – элементами 2 строки. 5. Запись матрицы в файл Индексы i2 и j2 распределены по диапазону [1..8], i3 – по диапазону [1..4]. Создать матрицу по следующему правилу 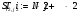 - чётные варианты; - чётные варианты; 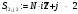 - нечётные варианты. - нечётные варианты.Создать вектор по следующему правилу 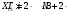 Создать вектор по следующему правилу 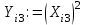 Получить матрицу А, первый столбец которой – Х, второй столбец – Y. Внимание! Необходимо именно получить по имеющимся данным, а не ввести с клавиатуры заново. Записать матрицу А в файл по формату: "ВАРИАНТ_ФАМИЛИЯ_СТУДЕНТА0" Матрицу S записать в файл по формату: "ВАРИАНТ_ФАМИЛИЯ_СТУДЕНТА1" Матрица R содержит квадраты элементов матрицы S. Матрицу R записать в файл по формату: "ВАРИАНТ_ФАМИЛИЯ_СТУДЕНТА2" Листинг в Matlab  clc; clear all; for i2=1:8 for j2=1:8 S(i2,j2)=1*i2+2020*j2 end end; for i3=1:4 X(i3,1)=2*2020+2*1; Y(i3,1)=X(i3).^2; end; A=[X Y]; fid = fopen('1_АвдеевА0.txt', 'wt'); % открыли файл для записи for j=1:2 for i=1:4 fprintf(fid,' %d', A(i,j)); end; fprintf(fid, '\n'); end; fclose(fid); fid = fopen('1_АвдеевА1.txt', 'wt'); % открыли файл для записи for j=1:8 for i=1:8 fprintf(fid,' %d', S(i,j)); end; fprintf(fid, '\n'); end; fclose(fid); fid = fopen('1_АвдеевА2.txt', 'wt'); % открыли файл для записи for j=1:8 for i=1:8 R(i,j)=S(i,j).^2; fprintf(fid,' %d', R(i,j)); end; fprintf(fid, '\n'); end; fclose(fid); Результат Файл 1_АвдеевА0.txt 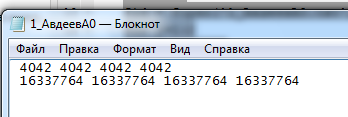 Файл 1_АвдеевА1.txt 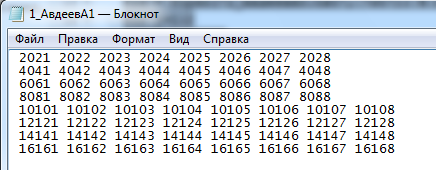 Файл 1_АвдеевА2.txt 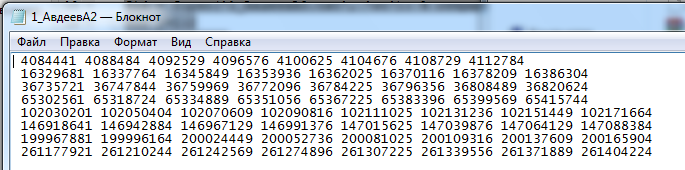 6. Чтение матрицы из файла Выполнить чтение данных из файла по формату: "ВАРИАНТ_ФАМИЛИЯ_СТУДЕНТА3" Файл создать вручную и заполнить произвольными значениями. Листинг в Matlab  clc; clear all; fid = fopen('1_АвдеевА3.txt', 'r'); % открыли файл для чтения formatSpec = '%d %f'; sizeA = [3 Inf]; A = fscanf(fid,formatSpec,sizeA); fclose(fid); disp(A); Файл 1_АвдеевА3.txt 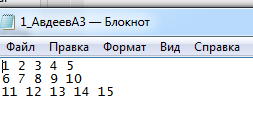 Результат 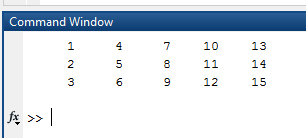 7. Арифметика с матрицами а) Сложение матриц Пусть 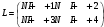 и и 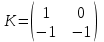 для нечётных вариантов; для нечётных вариантов;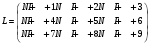 и и 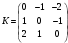 для чётных вариантов. для чётных вариантов.Вывести результаты: 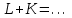 и и 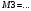 , если известно, что , если известно, что 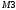 задана через индексированные элементы задана через индексированные элементы 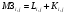 . .Листинг в Matlab  clc; clear all; L=[2020+1+1 2020+1+2 2020+1+3; 2020+1+4 2020+1+5 2020+1+5; 2020+1+7 2020+1+8 2020+1+9]; K=[0 -1 -2; 1 0 -1; 2 1 0]; %Сложение матриц disp('L+K='); disp(L+K); for i=1:3 for j=1:3 M3(i,j)=L(i,j)+K(i,j); end end; disp('M3='); disp(M3); Результат 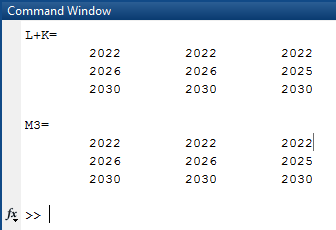 б) Вычитание матриц Пусть 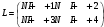 и и 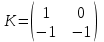 для нечётных вариантов; для нечётных вариантов;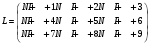 и и 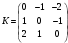 для чётных вариантов. для чётных вариантов.Вывести результаты: 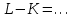 и и 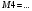 , если известно, что , если известно, что 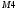 задана через индексированные элементы задана через индексированные элементы 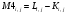 . .Листинг в Matlab  %Вычитание матриц disp('L-K='); disp(L-K); for i=1:3 for j=1:3 M4(i,j)=L(i,j)-K(i,j); end end; disp('M4='); disp(M4); Результат 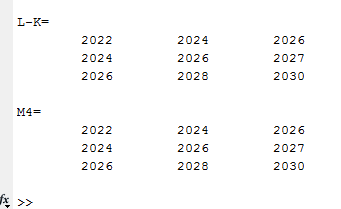 в) Сложение матрицы с константой Пусть 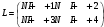 для нечётных вариантов; для нечётных вариантов;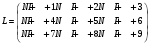 для чётных вариантов. для чётных вариантов.Вывести результаты: 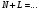 и и 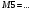 , если известно, что , если известно, что 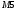 задана через индексированные элементы задана через индексированные элементы 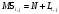 , где N – номер варианта обучающегося. , где N – номер варианта обучающегося.Листинг в Matlab  %Сложение матрицы с константой disp('1+L='); disp(1+L); for i=1:3 for j=1:3 M5(i,j)=1+L(i,j); end end; disp('M5='); disp(M5); Результат 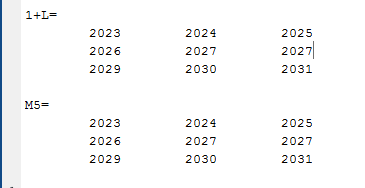 г) Перемножение матриц Пусть 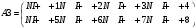 и и 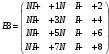 - для чётных вариантов; - для чётных вариантов;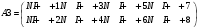 и и 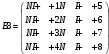 - для нечётных вариантов. - для нечётных вариантов. Выполнить умножение 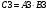 . . Получить тот же результат поэлементно с использованием соответствующих операторов. Листинг в Matlab  %Перемножение матриц A3=[1+2020+1 1+2020+3 1+2020+5 1+2020+7; 1+2020+2 1+2020+4 1+2020+6 1+2020+8]; B3=[1+2020+1 1+2020+5; 1+2020+2 1+2020+6 1+2020+3 1+2020+7 1+2020+4 1+2020+8]; disp('A3*B3='); disp(A3*B3); for i=1:2 for j=1:2 S=0; for k=1:4 S=S+A3(i,k)*B3(k,j); end; M5_1(i,j)=S; end end; disp('M5_1='); disp(M5_1); Результат  д) Умножение матрицы на константу Вывести -L. Пояснить уместность данного примера для рассмотрения умножения матрицы на константу. Получить матрицу 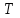 эквивалентную эквивалентную 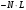 поэлементно. поэлементно.Листинг в Matlab  %Умножение матрицы на константу disp('-L='); disp(-1*L); for i=1:3 for j=1:3 T(i,j)=-1*L(i,j); end end; disp('T='); disp(T); Результат 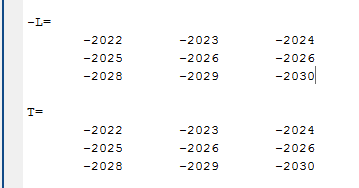 е) Определитель матрицы Вычислить определители (det) всех ранее созданных массивов, подходящих под условие расчёта определителя. Прокомментировать невозможность вычисления определителя для остальных массивов. Листинг в Matlab  %Определитель матрицы disp('Определитель L='); disp(det(L)); disp('Определитель K='); disp(det(K)); disp('Определитель M3='); disp(det(M3)); disp('Определитель M4='); disp(det(M4)); disp('Определитель M5='); disp(det(M5)); disp('Определитель M5_1='); disp(det(M5_1)); disp('Определитель T='); disp(det(T)); Результат 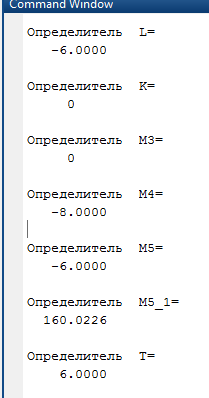 Остальные матрицы не квадратные, определитель для них не существует ж) Скалярное произведение векторов Пусть 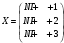 и и 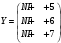 - для чётных вариантов; - для чётных вариантов;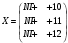 и и 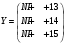 - для нечётных вариантов. - для нечётных вариантов.Перемножить скалярно 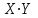 . . Вывести результат скалярного произведения. Проверить результат скалярного произведения поэлементно: 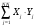 . .Где N – номер варианта обучающегося, NN – размерность вектора, Г – последняя цифра текущего года. Листинг в Matlab  % Скалярное произведение векторов X=[1+2020+10; 1+2020+11; 1+2020+12]; Y=[1+2020+13; 1+2020+14; 1+2020+15]; disp('(X,Y)='); disp(dot(X,Y)); S=0; for i=1:3 S=S+X(i)*Y(i); end disp('S='); disp(S); Результат 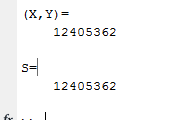 з) Векторное произведение векторов Пусть 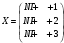 и и 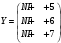 - для чётных вариантов; - для чётных вариантов;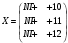 и и 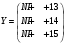 - для нечётных вариантов. - для нечётных вариантов.Получить векторное произведение векторов 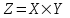 . Использовать cross. . Использовать cross.Формула для векторного произведения следующая: 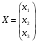 , , 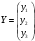 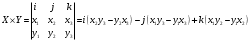 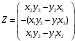 Проверить соотношения: 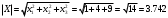 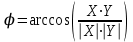 ; ; 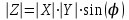 . .Рассчитать 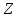 поэлементно. поэлементно.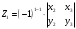 , , 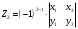 , , 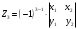 . . Листинг в Matlab  % Векторное произведение векторов disp('X x Y='); disp(cross(X,Y)); Z(1,1)=((-1).^(1-1))*det([X(2) X(3); Y(2) Y(3)]); Z(2,1)=((-1).^(2-1))*det([X(1) X(3); Y(1) Y(3)]); Z(3,1)=((-1).^(3-1))*det([X(1) X(2); Y(1) Y(2)]); disp('Z='); disp(Z); % Проверяем соотношения fi=acos(dot(X,Y)./(norm(X).*norm(Y))); disp('модуль Z='); disp(norm(Z)); disp('модуль Z по формуле='); disp(norm(X).*norm(Y).*sin(fi)); Результат  и) Суммирование элементов вектора Использовать функцию sum для нахождения суммы элементов векторов X и Y. Проверить результат суммированием элементов вектора через их индексы. Листинг в Matlab  % Суммирование элементов вектора disp('sum(X)='); disp(sum(X)); disp('sum(Y)='); disp(sum(Y)); Sx=0;Sy=0; for i=1:3 Sx=Sx+X(i); Sy=Sy+Y(i); end; disp('Сумма Х по элементно'); disp(Sx); disp('Сумма Y по элементно'); disp(Sy); Результат  к) След матрицы (сумма элементов на главной диагонали) Использовать функцию trace. Получить тот же результат с использованием операции суммирования. Листинг в Matlab  % След матрицы (сумма элементов на главной диагонали) disp('trace(L)='); disp(trace(L)); trL=0; for i=1:3 trL=trL+L(i,i); end; disp('След матрицы с использованием операции суммирования'); disp(trL); Результат  л) Векторизация Пусть 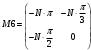 - для нечётных вариантов; - для нечётных вариантов;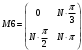 - для чётных вариантов. - для чётных вариантов. Векторизовать sin(M6). Прокомментировать полученный результат. Посчитать результат векторизации символьно и векторно. Листинг в Matlab  % Векторизация M6=[0 1*pi./3; 1*pi/3 1*pi]; disp('Векторизация sin(M6)='); disp(sin(M6)); for i=1:2 for j=1:2 V1_1(i,j)=sin(M6(i,j)); end end; disp('Векторизация по элементно'); disp(V1_1); disp('Векторизация векторно'); disp([sin(M6(:,1)) sin(M6(:,2))]); Результат  м) Обратная матрица Пусть 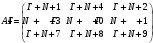 - для чётных вариантов, - для чётных вариантов,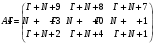 - для нечётных вариантов. - для нечётных вариантов. Вывести обратную к ней матрицу. Посчитать определитель матрицы. Листинг в Matlab  % Обратная матрица A4=[2020+1+9 2020+1+8 2020+1+7; 2020+1+3 2020+1+0 2020+1+1; 2020+1+2 2020+1+4 2020+1+1]; disp('Обратная матрица'); disp(inv(A4)); disp('Определитель обр матрица'); disp(det(inv(A4))); Результат  н) Единичная матрица Получить единичную матрицу 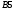 размерностью размерностью 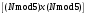 . .eye(Nmod 5) Проверить другие способы получения единичной матрицы: 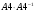 , , 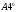 . .xmody – результат деления значения x на значение y. Листинг в Matlab  % Единичная матрица disp('Единичная матрица'); B5=eye(5,5); disp(B5); disp('Единичная матрица- другие способы получения '); A4_1=inv(A4); disp(A4*A4_1); disp(A4^0); Результат 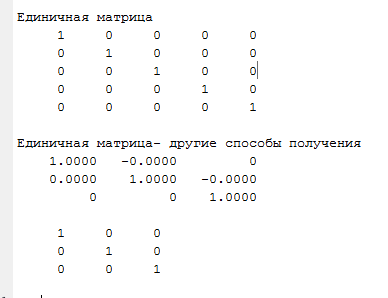 о) Трансформирование вектора в диагональную матрицу Пусть 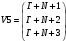 . . Получить в диагональную квадратную матрицу 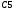 как результат выполнения функции: как результат выполнения функции: 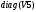 . .Листинг в Matlab  % Трансформирование вектора в диагональную матрицу V5=[2020+1+1;2020+1+2;2020+1+3]; disp('Диагональная матрица'); C5=diag(V5); disp(C5); Результат  п) Фрагментированные матрицы Выполнить фрагментацию матрицы 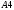 и получить матрицу и получить матрицу 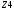 , в которой фигурируют 2-3 строки и 2-3 столбцы матрицы , в которой фигурируют 2-3 строки и 2-3 столбцы матрицы 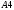 . .Выполнить фрагментацию матрицы 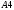 и получить матрицу и получить матрицу 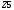 , в которой фигурируют 3 строка и 2-3 столбцы матрицы , в которой фигурируют 3 строка и 2-3 столбцы матрицы 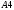 . .Выполнить фрагментацию матрицы 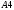 и получить матрицу и получить матрицу 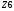 , в которой фигурируют 1-3 строки и 2 столбец матрицы , в которой фигурируют 1-3 строки и 2 столбец матрицы 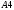 . .Z = A4([диапазон_строк], [диапазон_столбцов]) Листинг в Matlab  % Фрагментированные матрицы disp('Фрагментированные матрицы'); Z4=A4(2:3,2:3); disp('Z4='); disp(Z4); Z5=A4(3:3,2:3); disp('Z5='); disp(Z5); Z6=A4(1:3,2:2); disp('Z6='); disp(Z5); Результат  р) Склейка матриц по горизонтали Получить матрицу 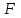 посредством склейки матриц посредством склейки матриц 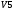 , , 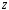 и и 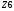 по горизонтали (horzcat). по горизонтали (horzcat).Листинг в Matlab  % Склейка матриц по горизонтали F=horzcat(V5,Z,Z6); disp('F='); disp(F); Результат  с) Склейка по вертикали Получить матрицу 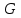 посредством склейки матриц посредством склейки матриц 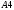 и и 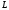 по вертикали (vertcat). по вертикали (vertcat).Листинг в Matlab  % Склейка матриц по вертикали G=vertcat(A4,L); disp('G='); disp(G); Результат 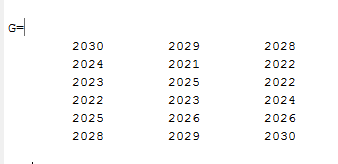 т) Сортировка по столбцу Для нечётных вариантов выполнить сортировку полученной матрицы 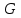 по элементам указанного 3-го столбца. по элементам указанного 3-го столбца.Для чётных вариантов выполнить сортировку полученной матрицы 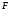 по элементам указанного 2-го столбца. по элементам указанного 2-го столбца. Листинг в Matlab  % Сортировка по столбцу disp('Сортировка по 3 столбцу'); disp(sortrows(G,3)); Результат  у) Сортировка по строке Для нечётных вариантов выполнить сортировку полученной матрицы 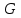 по элементам указанной 6-й строки. по элементам указанной 6-й строки. Для чётных вариантов выполнить сортировку полученной матрицы 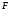 по элементам указанной 3-й строки. по элементам указанной 3-й строки. Листинг в Matlab  % Сортировка по строке disp('Сортировка по 6 строке'); G1=sortrows(G',6); disp(G1'); Результат 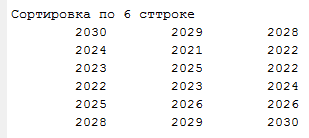 ф) Обычная сортировка элементов вектора Пусть 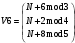 . . Выполнить обычную сортировку 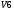 с использованием функции с использованием функции 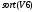 . xmody – результат деления значения x на значение y. . xmody – результат деления значения x на значение y.Листинг в Matlab  % Обычная сортировка элементов вектора V6=[1+mod(6,3);1+mod(2,4);1+mod(8,5)]; disp('Обычная сортировка'); disp(sort(V6)); Результат  х) Инверсия элементов вектора Пусть 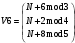 . . Инвертировать матрицу  . xmody – результат деления значения x на значение y. Применить fliplr и flipud, выполнив предварительно необходимые преобразования. . xmody – результат деления значения x на значение y. Применить fliplr и flipud, выполнив предварительно необходимые преобразования.Листинг в Matlab  % Инверсия элементов вектора disp('Инверсия элементов вектора слева направо'); disp(fliplr(V6')); disp('Инверсия элементов вектора сверху вниз'); disp(flipud(V6)); Результат  8. Решение СЛАУ Решить СЛАУ через матрицы: - методом Крамера; - методом обратной матрицы. Решить СЛАУ через символику. Применив к расчётам функции «sym» и «syms». 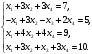 Листинг в Matlab  clc; clear all; A=[1 3 0 3; -1 3 -1 2; 1 4 0 4; 1 3 1 3]; b=[7;5;9;10]; % Решение методом Крамера A1=A;A2=A;A3=A;A4=A; A1(:,1)=b; A2(:,2)=b; A3(:,3)=b; A4(:,4)=b; x1(1,1)=det(A1)./det(A); x1(2,1)=det(A2)./det(A); x1(3,1)=det(A3)./det(A); x1(4,1)=det(A4)./det(A); disp('Решение методом Крамера'); disp(x1); disp('Решение методом обратной матрицы'); x2=inv(A)*b; disp(x2); % Решить СЛАУ через символику syms x1 x2 x3 x4; X=[x1;x2;x3;x4]; E=A*X-b; X=solve(E); disp('Решение СЛАУ через символику'); disp(double(X)); Результат 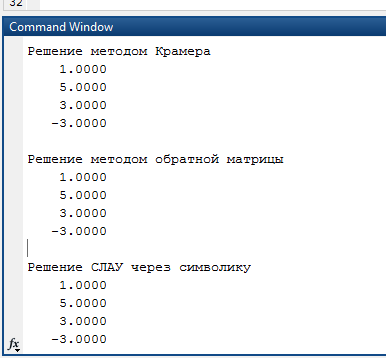 Варианты задания (согласно номеру обучающегося в списке учебной группы):
|