Вариант №12 профильного ЕГЭ по математике 2023. Вариант 12 - 2023. Вариант 12 2023 в треугольнике угол равен 90, высота, угол равен 60. Найдите. 2
 Скачать 414.88 Kb. Скачать 414.88 Kb.
|
|
Вариант №12 − 2023 1 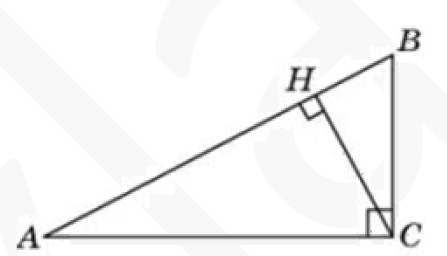 . В треугольнике . В треугольнике 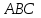 угол угол 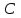 равен 90°, равен 90°, 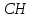 − высота, угол − высота, угол  равен 60°, равен 60°, 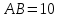 . Найдите . Найдите 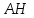 . .2 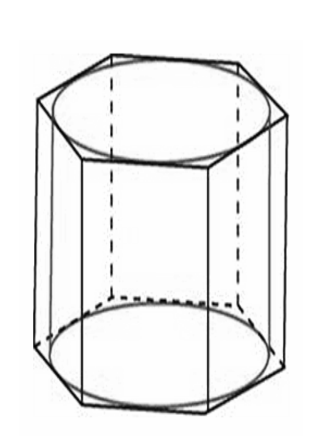 . Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен . Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен 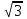 , если известно, что высота призмы равна 6. , если известно, что высота призмы равна 6.3. У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей. 4.Вероятность того, что батарейка бракованная, равна 0,04. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными. 5. Решите уравнение 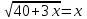 . Если уравнение имеет более одного корня, укажите меньший из них. . Если уравнение имеет более одного корня, укажите меньший из них.6. Найдите значение выражения 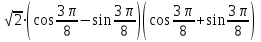 . .7 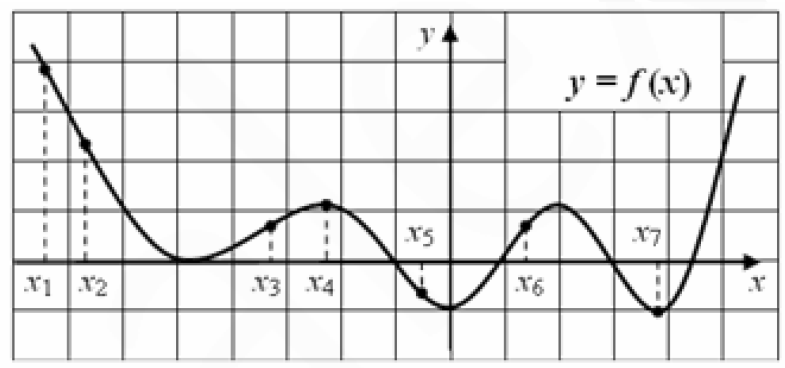 . На графике дифференцируемой функции . На графике дифференцируемой функции 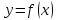 отмечены семь точек: отмечены семь точек: 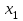 , , 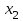 , ..., , ..., 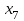 . Найдите все отмеченные точки, в которых производная функции . Найдите все отмеченные точки, в которых производная функции 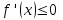 . В ответе укажите количество этих точек. . В ответе укажите количество этих точек.8 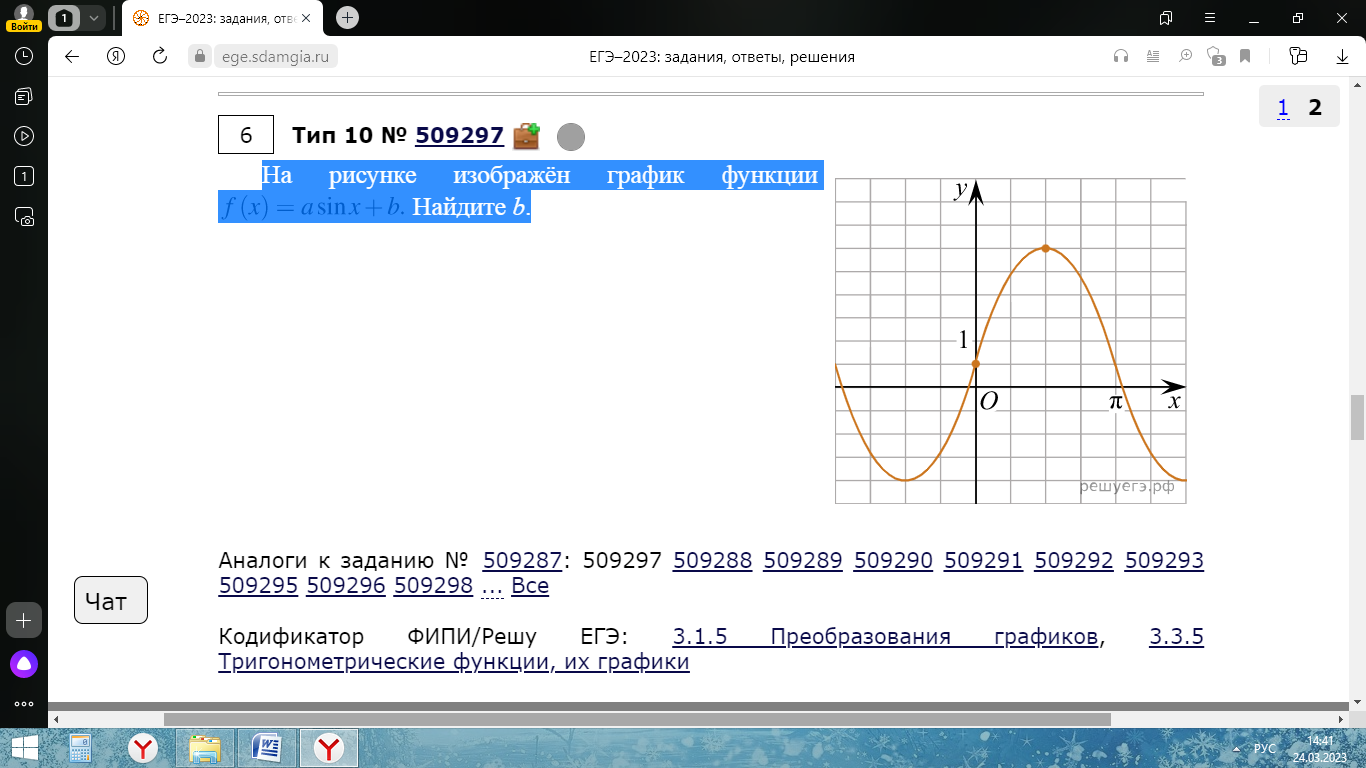 . Высота над землёй подброшенного вверх мяча меняется по закону . Высота над землёй подброшенного вверх мяча меняется по закону 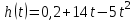 , где , где 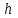 − высота в метрах, − высота в метрах, 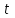 − время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 метров? − время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 метров? 9. Имеется два сплава. Первый сплав содержит 5% меди, второй − 95% меди. Масса второго сплава меньше массы первого на 90 кг. Из этих двух сплавов получили третий сплав, содержащий 45% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. 10. На рисунке изображён график функции 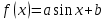 . Найдите . Найдите 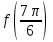 . .11. Найдите точку минимума функции 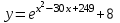 . .=============================== 12. а) Решите уравнение 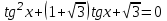 . .б) Найдите все корни этого уравнения, принадлежащие отрезку 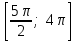 . .13. В правильной шестиугольной призме 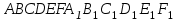 все рёбра равны 1. все рёбра равны 1.а) Докажите, что плоскости 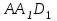 и и 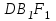 перпендикулярны. перпендикулярны.б) Найдите тангенс угла между плоскостями 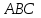 и и 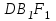 . .14. Решите неравенство 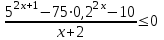 . .15.15-го декабря 2018 года Саша и Паша взяли в банке одинаковые суммы в кредит на 12 месяцев. Банк предложил им похожие схемы погашения долга. Условия возврата кредита у Саши оказались следующие: - 1-го числа каждого месяца долг возрастает на 10% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число месяца необходимо выплачивать одним платежом часть долга; - на 15-е числа каждого следующего месяца долг должен быть на одну и туже сумму меньше долга, чем на 15-е число предыдущего месяца. У Паши условия возврата кредита были таковы: - 1-го числа каждого месяца долг возрастает на 10% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число месяца необходимо выплачивать одним платежом часть долга; - на 15-е число каждого месяца с января по ноябрь включительно долг должен уменьшаться на 50 тыс. рублей; - в декабре 2019 года весь оставшийся на тот момент долг должен быть полностью погашен. Когда в декабре 2019 года Саша и Паша рассчитались со своими кредитами, выяснилось, что один из них выплатил за год банку на 429 тыс. рублей больше, нежели другой. Определите, какая сумма была взята в кредит каждым из них. 16. Медиана 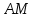 треугольника треугольника 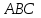 продолжена за точку продолжена за точку 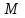 на расстояние на расстояние 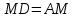 . .а) Докажите, что 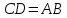 . .б) Найдите площадь треугольника 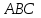 , если , если 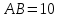 , , 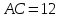 , , 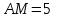 . .17. Найдите все значения 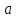 , при каждом из которых система уравнений , при каждом из которых система уравнений 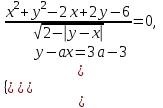 имеет ровно одно решение. имеет ровно одно решение.18. По кругу в некотором порядке по одному разу написаны натуральные числа от 9 до 18. Для каждой из десяти пар соседних чисел нашли их наибольший общий делитель. а) Могло ли получиться так, что все наибольшие общие делители равны 1? б) Могло ли получиться так, что все наибольшие общие делители попарно различны? в) Какое наибольшее количество попарно различных наибольших общих делителей могло при этом получиться? |
