Вариант 2 +. Вариант 2 Задача 1
 Скачать 54.11 Kb. Скачать 54.11 Kb.
|
|
Вариант №2 Задача №1 На основании следующих данных произведите группировку по годовому товарообороту, разделив всю совокупность магазинов на три группы. По каждой группе рассчитайте среднесписочную численность работников в среднем на один магазин. Сведите данные в таблицу и сделайте соответствующие выводы.
Решение: Произведем группировку по годовому товарообороту. Определим величину интервала по формуле h = Xmax – Xmin/n 2912-700/3 = 737 1 группа – 700 - 1437 – 9 магазинов 2 группа – 1437 – 2174 – 6 магазинов 3 группа – 2174 – 2912 – 15 магазинов
Вывод: Как видно из таблицы самой многочисленной является третья группа, следовательно в ней самый большой товарооборот и самое больше число сотрудников в среднем на 1 магазин. Самой малочисленной является вторая группа, однако среднесписочное число сотрудников и годовой товарооборот в ней выше чем в первой группе. Задача №2 Добыча нефти и угля во 2 квартале 2016 года характеризуется следующими данными:
Теплота сгорания нефти45,0 мДж/кг, угля-26,8 мДж/кг. Сделайте пересчёт в условное топливо (29,3 Мдж/кг) и проведите анализ изменения совокупной добычи этих ресурсов. Решение Имеем теплоту сгорания : Нефти- 45 мдж/кг; угля – 26,8 мДж/кг. Определим коэффициенты пересчёта в условное топливо: Для нефти - = 1,5358 Для угля - = 0,9146 С учётом пересчёта:
По исходным данным: Добыча нефти за три месяца:23,8+25+24,2=73 Добыча угля 23,2+20,0+18,7=62,1 х 100% = 117,55% Угля добыто на 55% больше, чем нефти. Совокупная добыча нефти в перерасчёте на условное топливо за три месяца: 36,55+38,40+17,10= 112,12 Угля : 21,22+18,47+17,10=56,8 После перерасчёта на условное топливо ,при сравнении двух совокупностей ресурсов превышение добычи нефти составило 97, 39% Задача №3 Денежные доходы населения в регионе по месяцам в ценах 2018 г. (в расчете на душу населения, руб.) составили:
Постройте радиальную диаграмму денежных доходов населения 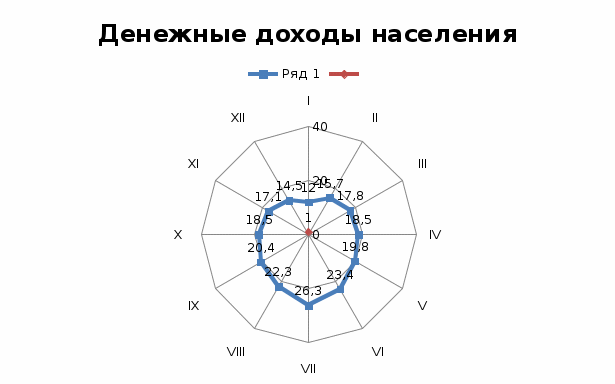 Задача №4 В прошлом году объём грузооборота по грузовому автотранспортному предприятию составил 341 млн. т/км. Планом текущего года было предусмотрено довести объём грузооборота до 352 млн. т/км. Фактический объём грузооборота в текущем году составил 362 млн. т/км. Определить: относительную величину планового задания по росту грузооборота; относительную величину динамики грузооборота; относительную величину выполнения плана по грузообороту. Решение: У0 = 341 млн. т/км. Упл. = 352 млн. т/км. У1 = 362 млн. т/км. 1) ОВПЗ = Упл./У0 = 352/341 = 1,03 или 103,0% Следовательно по плану предусмотрено увеличение грузооборота на 3% (103-100) 2) ОВД = У1/У0 = 362/341 = 1,06 или 106,0% Следовательно, фактически по сравнению с прошлым годом грузооборот повысился на 6% (106-100) 3) ОВВП = У1/Упл = 362/352 =1,02 или 102,0% Т.е. план по размеру грузооборота превышен на 4% (106-102) Задача№ 5 Дан ряд чисел:18; 15;22; 14; 12; 14;15; 14. Найдите размах, среднее арифметическое, медиану и моду этого ряда. Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел 22-12=10 Среднее арифметическое данного ряда находим по формуле средней арифметической простой: 18+15+22+14+12+14+15+14/8 = 15,5 Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12;14;14;14;15;15;18;22 Медиана четного ряда чисел находится путем вычисления средней арифметической двух цифр, стоящих посередине ряда: Ме = (14+15)/2 = 14,5 Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других Мо=14 Задача №6. По данным обследования получено следующее распределение студентов-заочников по возрасту на разных факультетах.
Рассчитайте на юридическом факультете: ♦ средний возраст студента-заочника; ♦ модальное значение; ♦ медиану. Решение: В данном ряду варианты усредняемого признака (возраст студента) представлены не одним числом, а в виде интервала «от – до». Причём последний – интервал открытый. В таких рядах условно принимается, величина интервала последней группы равна величине интервала предыдущей. Таким образом, возраст студента в последней группе равен 45-49 Исчисление средней по сгруппированным данным производится по формуле средней арифметической взвешенной: 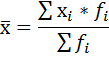 Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала. 20+25/2 = 22,5 26+30/2 = 28 31+35/2 = 33 36+40/2 = 38 45+49/2 = 47
Дальнейший расчёт производится обычным методом определения средней арифметической взвешенной: Х= Σxf\Σf 61235/2055 = 29,7 Средний возраст студента-заочника на факультете естествознания равен 29,7 годам. Модальное значение В интервальных рядах распределения с равными интервалами мода определяется по формуле: 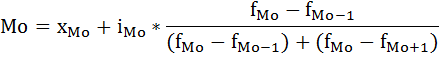 xMo – начальное значение интервала, содержащего моду; iMo – величина модального интервала, fMo – частота модального интервала, f(Mo-1)– частота интервала, предшествующего модальному, f(Mo+1) – частота интервала, следующего за модальным. Сначала определим модальный интервал: Наибольшее число студентов 850, возраст студентов 31-35. Следовательно, этот интервал является модальным интервалом ряда распределения. xMo – 31 iMo – 4 fMo – 850 f(Mo-1) - 800 f(Mo+1) - 100 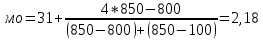 ♦ медиана Медиана интервального вариационного ряда распределения определяется по формуле: 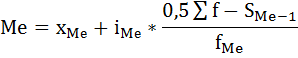 где xMе– начальное значение интервала, содержащего медиану; iMе – величина медианного интервала; Σf – сумма частот ряда; S(Me-1)– сумма накопленных частот, предшествующих медианному интервалу; fMe– частота медианного интервала. Определим, прежде всего, медианный интервал. Сумма накопленных частот, превышающая половину всех значений (720), соответствует интервалу 31-35. Это и есть медианный интервал, в котором находится медиана. xMе – 31 iMе – 4 Σf – 2055 S(Me-1) - 1100 fMe - 850 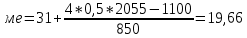 Задача №7 Цена и выручка от реализации по трем коммерческим магазинам.
Логическая формула средней: 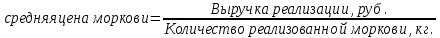 нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови. Искомая средняя определяется по средней гармонической взвешенной: 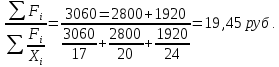 Теоретический вопрос: Какие Вы знаете основные программно-методологические вопросы статистического наблюдения? Цель статистического наблюдения определяется исходя из общих задач, поставленных перед статистическим изучением явлений. Объект статистического наблюдения - это та совокупность, о которой должны быть собраны нужные сведения. Единица наблюдения - это элемент объекта наблюдения, который является носителем признаков, подлежащих регистрации. Программа статистического наблюдения - это перечень признаков, регистрируемых в процессе наблюдения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
