Тер Мех. Вариант 25++. Вариант 25. К125

• Название: Вариант 25. К125
• Анкор: Тер Мех
• Дата: 10.02.2022
• Размер: 0.59 Mb.
• Имя файла: Вариант 25++.doc
• Тип: Решение; #357556

Вариант 25.

К1-25

По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t= t₁(с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Уравнения движения точки М

x= 2cos(p t² /3) - 2,см y= - 2 sin(p t² /3) + 3, см t₁=1c ( Рис.1)

Решение.

1. Для определения уравнения движения траектории точки, исключим из

заданных уравнений движения точки – время t . Из условия известно, что координаты движения точки задаются уравнениями

x= 2cos(p t² /3) - 2,см y= - 2 sin(p t² /3) + 3,

(1)

Преобразуем зависимости /1/ следующим образом

cos(p t² /3)= ; sin(p t² /3) = ;

cos²(p t² /3)=( )² ; sin²(p t² /3) =( )² ;

cos²(p t² /3) + sin²(p t² /3) =( )² +( )² =1;

(x+2) ² + (y-3)²=2²;
Т.е. уравнение движения (2)

(x+2) ² + (y-3)²=2²;Окружность с центром в т.О(-2;3),радиус R=2см.
2.Скорость точки найдем по ее проекциям на координатные оси:

[ 2cos(p t² /3) - 2]'_t = (3)

[- 2 sin(p t² /3) + 3]'_t = (4)
Общая скорость определяется по формуле

(5)
Определим V_X и V_Y из /3/ и /4/ при t₁ =1 c
V_X = -3.63 см/с (6)

V_Y = -2.09 см/с

Из (5) имеем

3. Аналогично найдем ускорение точки:

a_x = [ ]'_t =

[ ]'_t = ( 7 )

Общее ускорение определяется по формуле

(8)

Определим a_X и a_Y из / 7 / при t₁ =1 c
a_X = -8.00 см/с² ; (9)

a_Y = 7.59 см/с² ;

Из ( 8 ) имеем

(10)

4. 
   Касательное ускорение найдем, дифференцируя по времени равенство
   

получим



или

( 11)

Числовые значения всех величин входящих в правую часть выражений (10), определены

и даются равенствами ( 6 ) и ( 9 ). Подставив в (11) эти числа, определим, что при t₁ = 1 c
(12)

4. 
   Нормальное ускорение точки
   

(13)

Подставляя в формулу (13) найденные числовые значения (10) и (12)

a и a , получим, что при t₁ = 1 c

4. 
   Радиус кривизны траектории определяем из формулы
   

Подставляем сюда числовые значения V и a_n , найдем, что при t₁ = 1 c


Ответ: Итак, движение точки начинается из т.Мо (x= 0 см; y= 3 см), при

t = 1с точка займет положение в т.М₁ (x= - 1 см; y= 1.27 см).

Координаты, см		Скорость, см/с			Ускорение, см/с2					Радиус кривизны, см
x	y	Vx	Vy	V	ax	ay	a	a	an
-1	1.27	-3.63	-2.09	4.19	-8.00	7.59	11.03	3.14	10.57	1.66

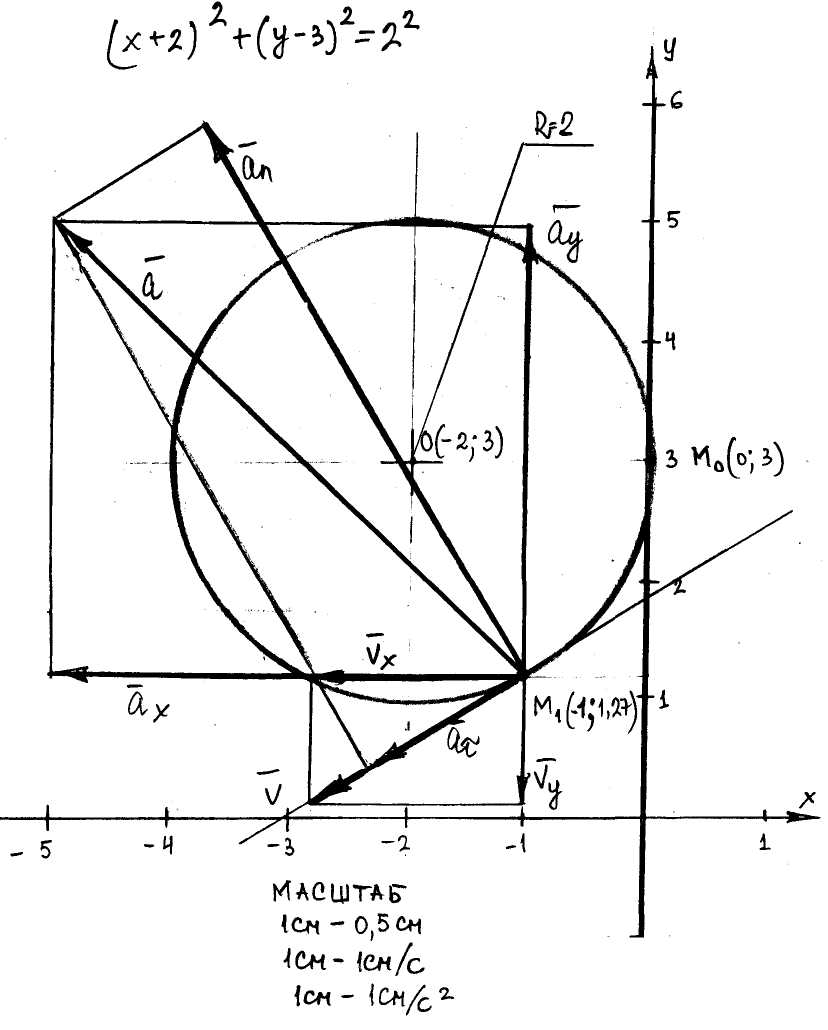рисунок 1

K2-25

Требуется для заданного положения механизма определить скорости и ускорения точек В и С, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат. Необходимые для расчета исходные данные приведены в таблице 1, схема механизма на рис.1.

№ вар.	Размеры в см				wOA, с-1	wI, с-1	eOA, с-1	nA, см/с	aA, см/с2
	OA	r	AB	AC
25	20	-	50	15	4	-	6	-	-

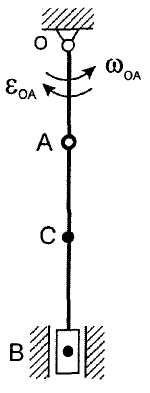Рисунок 1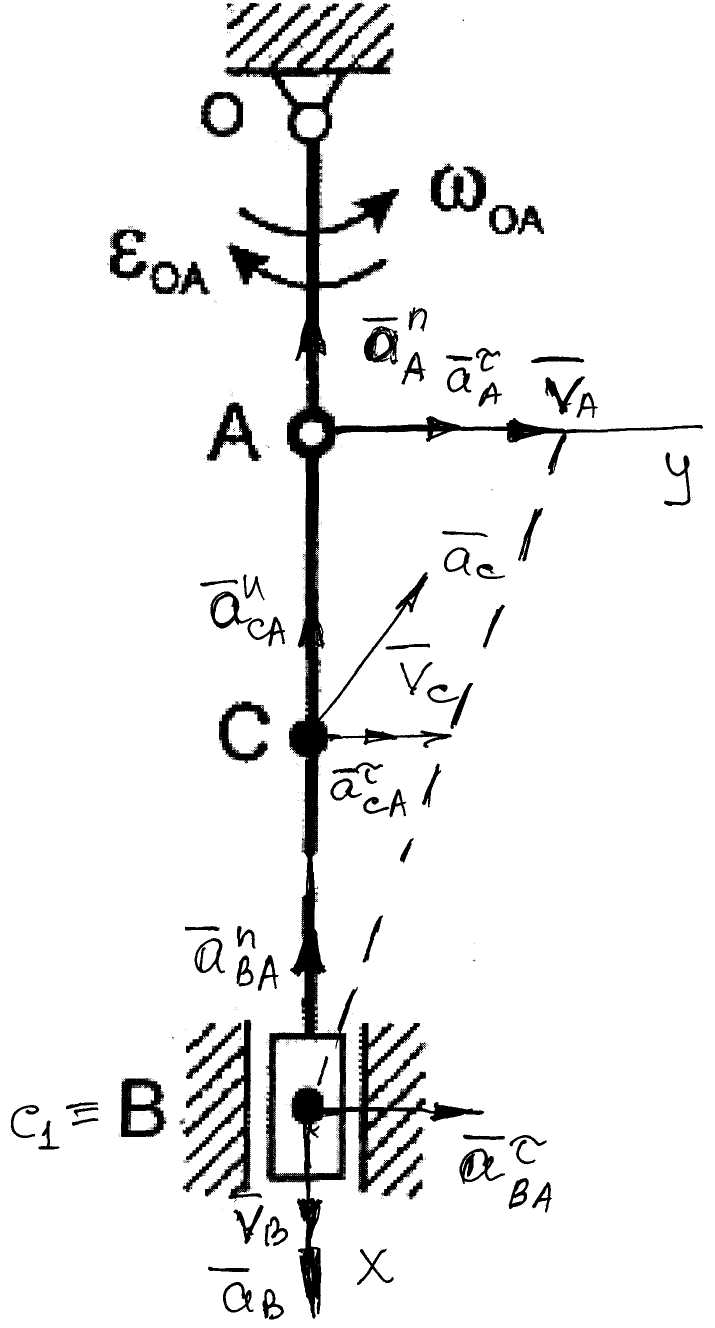



Рисунок 2


Решение.

Механизм совершает плоскопараллельное движение (рисунок 2).Найдем МЦС (мгновенный центр скоростей) стержня АВ. Для этого восстановим перпендикуляры из точек Аи В ( ).

Точка С₁есть МЦС. Поскольку , то точка С₁ совпадает с точкой В. МЦС стержня АВ есть точка В.

Поскольку , а точка С1ºВ МЦС, то по теореме о равенстве проекций скоростей точек А и В на стержень АВ, получим



Определим



Точка В есть МЦС стержня АВ.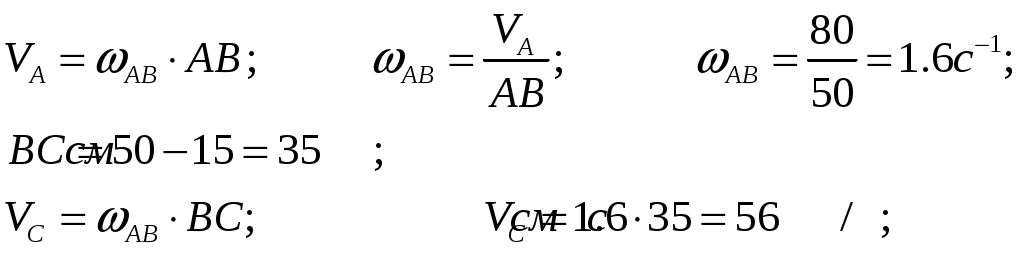



Определим ускорение точки В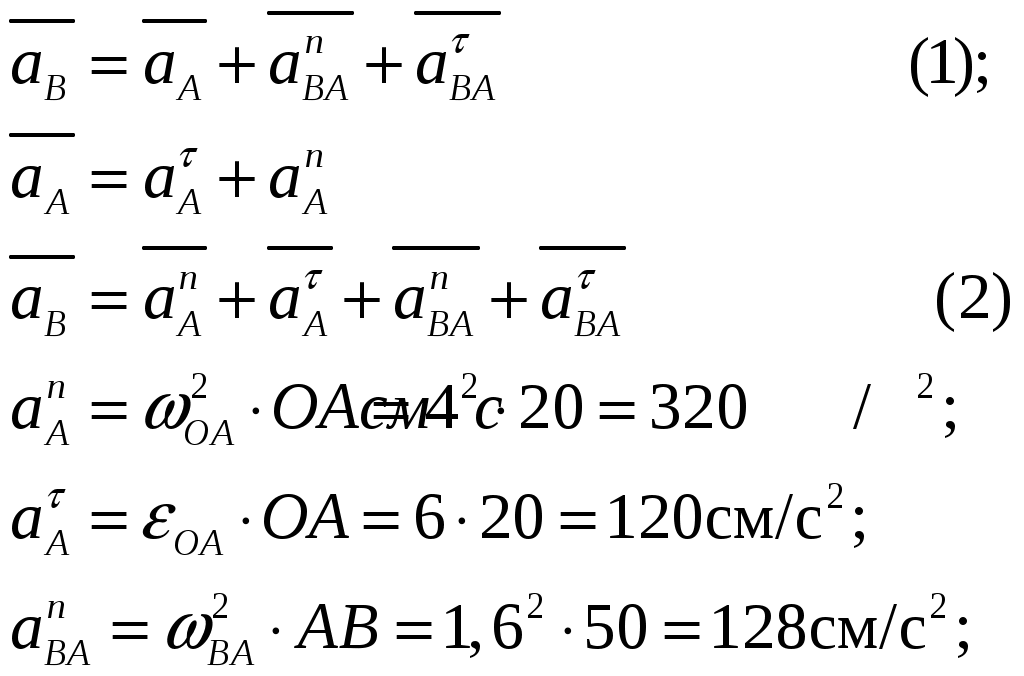



Введем систему координат ХВУ.

Спроецируем векторное равенство (2) на ось Х.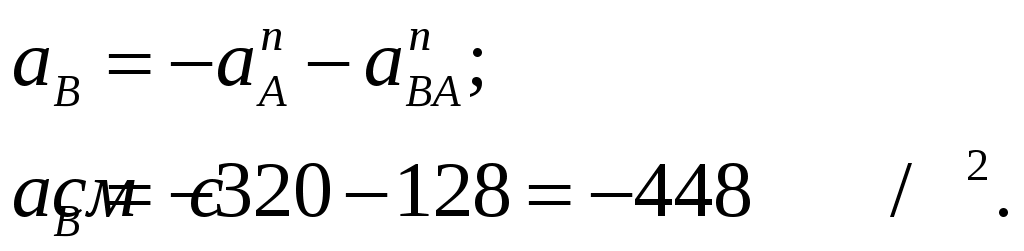



Спроецируем векторное равенство (2) на ось У.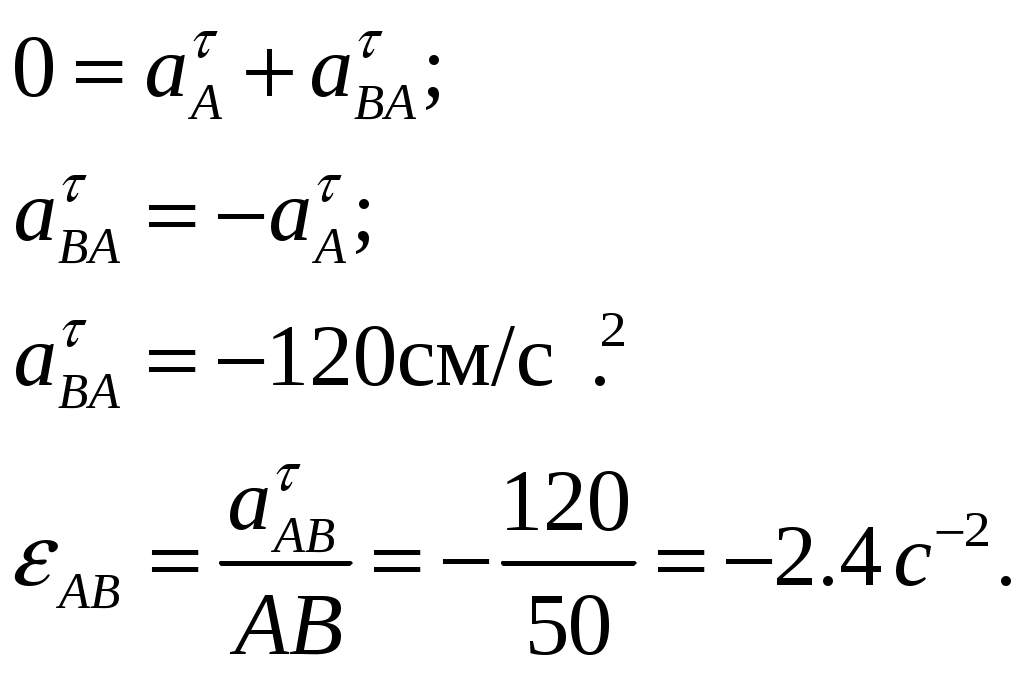



Определим ускорение точки С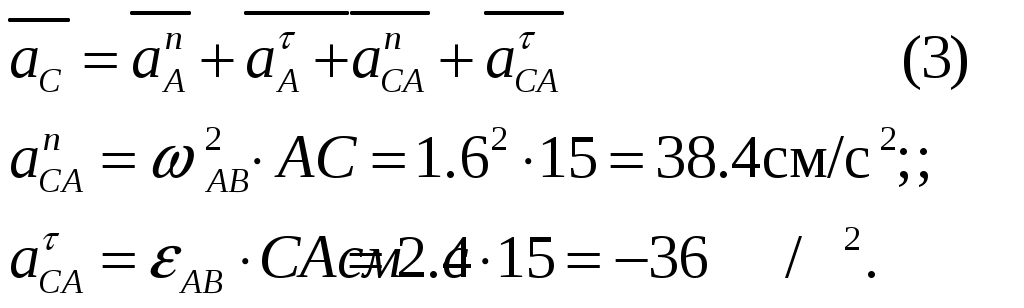



Спроецируем векторное равенство (3) на ось Х.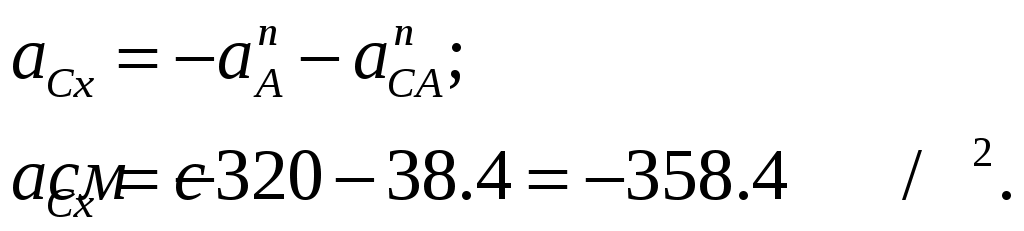



Спроецируем векторное равенство (3) на ось У.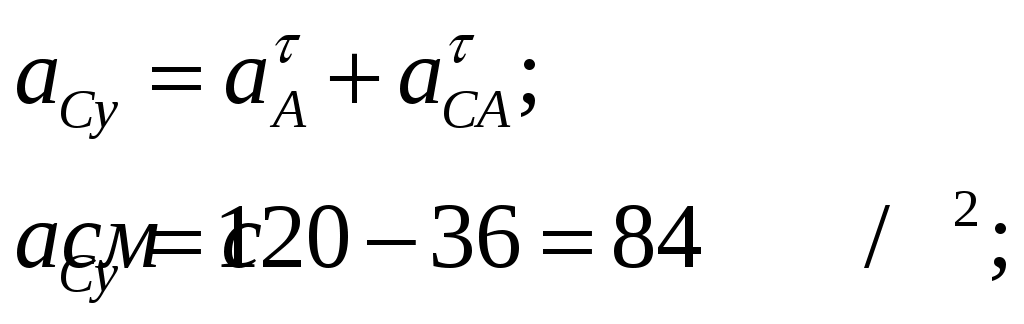




Ответ: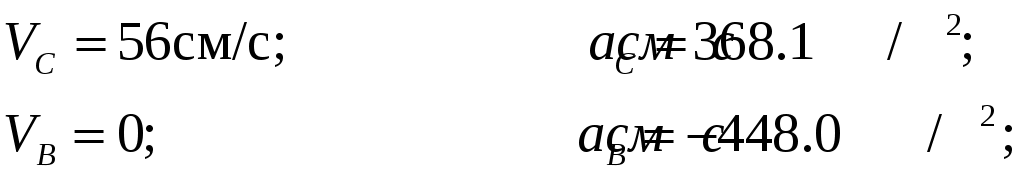


K3-25
Прямоугольная пластинка вращается вокруг неподвижной оси О₁О₂по закону =f(t), ось О₁О₂перпендикулярна плоскости чертежа. Положительное направление отсчета угла показано стрелкой. По пластинке движется точка М с законом движения OM = f₁(t). В момент времени t= 1 с определить абсолютную скорость (v_a) и абсолютное ускорение (а_а ) точки М. Данные для решения задачи приведены в таблице 1 и на рис.1.

№ вар	 = f(t), рад	S=OM=f1(t),м	b, м	R, м
25			0.2	-

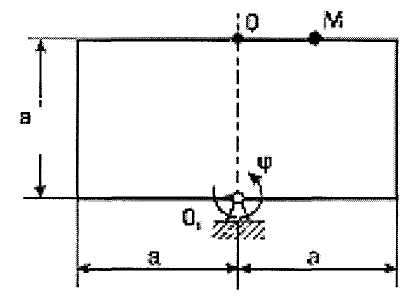Рисунок 1.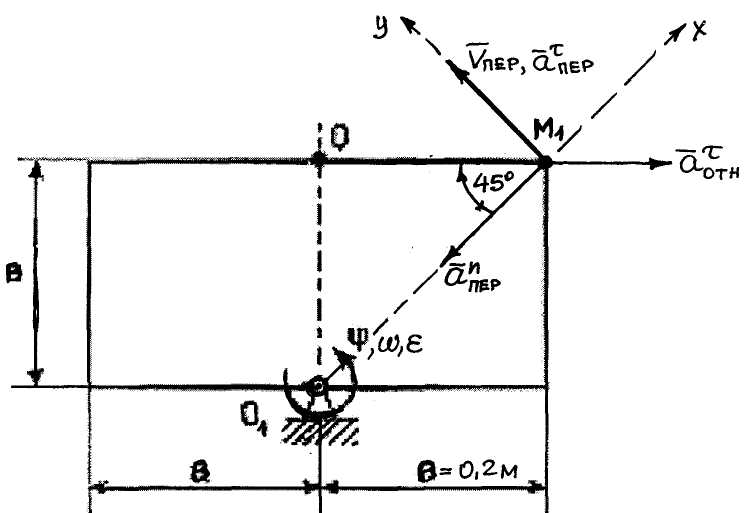







Рисунок 2

Решение. Точка М совершает сложное движение. Движется относительно прямоугольной пластинки и вместе с ней вращается вокруг оси О₁О₂. Тогда

движение точки относительно пластинки будет относительным, движение вместе с ней - переносным. Будем считать, что в заданный момент времени плоскость чертежа совпадает с плоскостью прямоугольной пластинки. Положение точки М на пластинке определяется расстоянием s_r = ОМ.

Абсолютную скорость точки М найдем как геометрическую сумму относительной и переносной скоростей

;

Абсолютное ускорение точки М

, где

; (1)

Определим все характеристики относительного и переносного движения

1. Относительное движение. Это движение происходит по закону

(2)

Сначала установим, где будет находиться точка М на момент времени

t₁ = 1 c .

Полагая в уравнении (2) t₁ = 1 c , получим

м

Изображаем на рис.1 точку в положении, определяемым этим числом

/ точка М /.

Находим числовые значения при t₁ = 1 c .







радиус кривизны относительно траектории точки М в момент времени t₁ = 1c.

Здесь _ОТН=


м/с²



; ; ;

При t=1c

c^-1; ;

2. Переносное движение. Это движение / вращение / происходит по закону

; ;
Для определения V_ПЕР и а_ПЕР найдем расстояние h до точки М₁ от оси вращения О₁О₂ .

тогда в момент времени t₁= 1 c , учитывая равенство /4/
V_ПЕР = | ω | ·h =0,4·0,28=0,113 м/с
а^τ _ПЕР = ε · h =1,2+0,28=0,339 м/с²;
аⁿ _ПЕР = ω² · h =0,4² ·0,28 =0,045м/с²;

Изображаем на рис.1 вектор V_ПЕР с учетом направления ω и вектор аⁿ _ПЕР

/ направлен к оси вращения /.
3. Кориолисово ускорение. Так как относительная траектория – плоская кривая и перемещается все время в своей плоскости, в этом при t₁ = 1c

а_КОР = 2·| ω V_ОТН | ·sin ;

Поскольку а_КОР = ω V_ОТН есть векторное произведение, то направление а_КОР можно найти, повернув вектор относительной скорости на 90⁰ в сторону переносного вращения
а_КОР = 2·0,4·0=0;
4. Определение . Так как ,определим V_АБС

V_АБС = 0+0,113=0,113м/с

5. Определение а_АБС . По теореме сложения ускорений, так как


Для определения проведем координатные оси М₁ХУ / рис.1 /

и вычислим проекции вектора на эти оси.

Учтем при этом, что вектор а_КОР лежит на проведенной оси Х , а векторы а^τ_{ОТН ,} V_ОТН расположены на проведенной оси У. С учетом этих равенств /3/,/5/,/6/
а_АБСx = м/с²
а_АБСy = м/с²

Отсюда находим значение а_АБС в момент времени t₁ = 1 c



Ответ: V_АБС = 0,113м/с; а_АБС =1,691м/с²;


C1-25
Дано: конструкция, состоящая из двух частей соединенных в точке Eшарниром (рис. 1.), удерживается двумя неподвижными шарнирными опорами в точках А и C.

Конструкция нагружена сосредоточенной силой F= 3 кН, парой сил с моментом М =8 кНм и равномерно распределенной нагрузкой мощностью

q = 7 кН/м; α = 30°. Определить реакции опор А и C, а также шарнира E.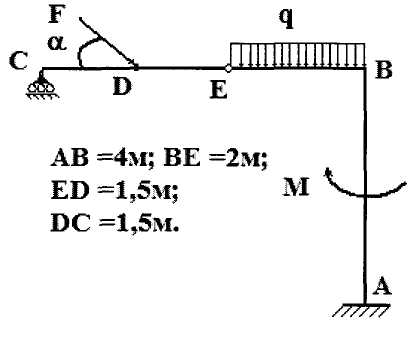







рисунок 1
Решение.

Освобождаем конструкцию от связей, т.е. убираем опоры, заменяя их действие неизвестными силами в точках А и C(рис. 2).

Для упрощения вычисления момента силы F разложим ее на вертикальную F_y и горизонтальную составляющие F_x (рис. 2 и 3):

F_X = F'= F·cos 30º . F_Y= F''= - F·sin 30º
Для всей конструкции (рисунок 2)

Σ_iA =0

- M_A – M – Y_C·5 + F·sin 30º ·3.5 + Q ·1 =0 (1)

После подстановки данных и вычислений уравнение (1) примет вид

- M_A -8 – Y_C·5 + 3 ·sin 30º ·3.5+ 7·2·1 =0

- М_А + Y_C·5 + 15.09 =0

М_А = 15.09 - Y_C·5 (2)
Рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира E(рис. 3, a)

Σ M =0; -Y_С·3 + F·sin30º ·1.5 = 0 (3)

Y_С = 1.3 кН
ΣY_i=0; Y_C +Y_E – F·sin 30º =0 (4)
Y_E = - Y_C + F·sin 30º = - 1.3 +3 · sin 30 º = 1.3 кН
Из (2) М_A= 15.09 – Y_C ·5 = 15.09 – 1.3·5 = 8.59 кНм

Для правой части конструкции (рисунок 3,б)
ΣY_i=0; Y_A – Y_E – Q =0 (5)

Y_A = Y_E + Q = 1,3 +7·2 =15,3кН
ΣM_iE=0; Y_A ·2 + X_A·4 – M_A – M – Q·1 = 0 (6)


X_A = = =0
ΣX_i =0 X_A – X_E=0 (7)
X_E = X_A =0
Модули реакций опор А,С и шарнира E
R_A= = = 15.3 кН

R_E = = = 1.3 кН

R_C = Y_C=1.3 кН

Результаты расчетов сведем в таблицу 1.

Силы, кН. Момент ,кНм
XA	YA	RA	MA	YC	RC	XE	YE	RE
0	15.3	15.3	8.59	1.3	1.3	0	1.3

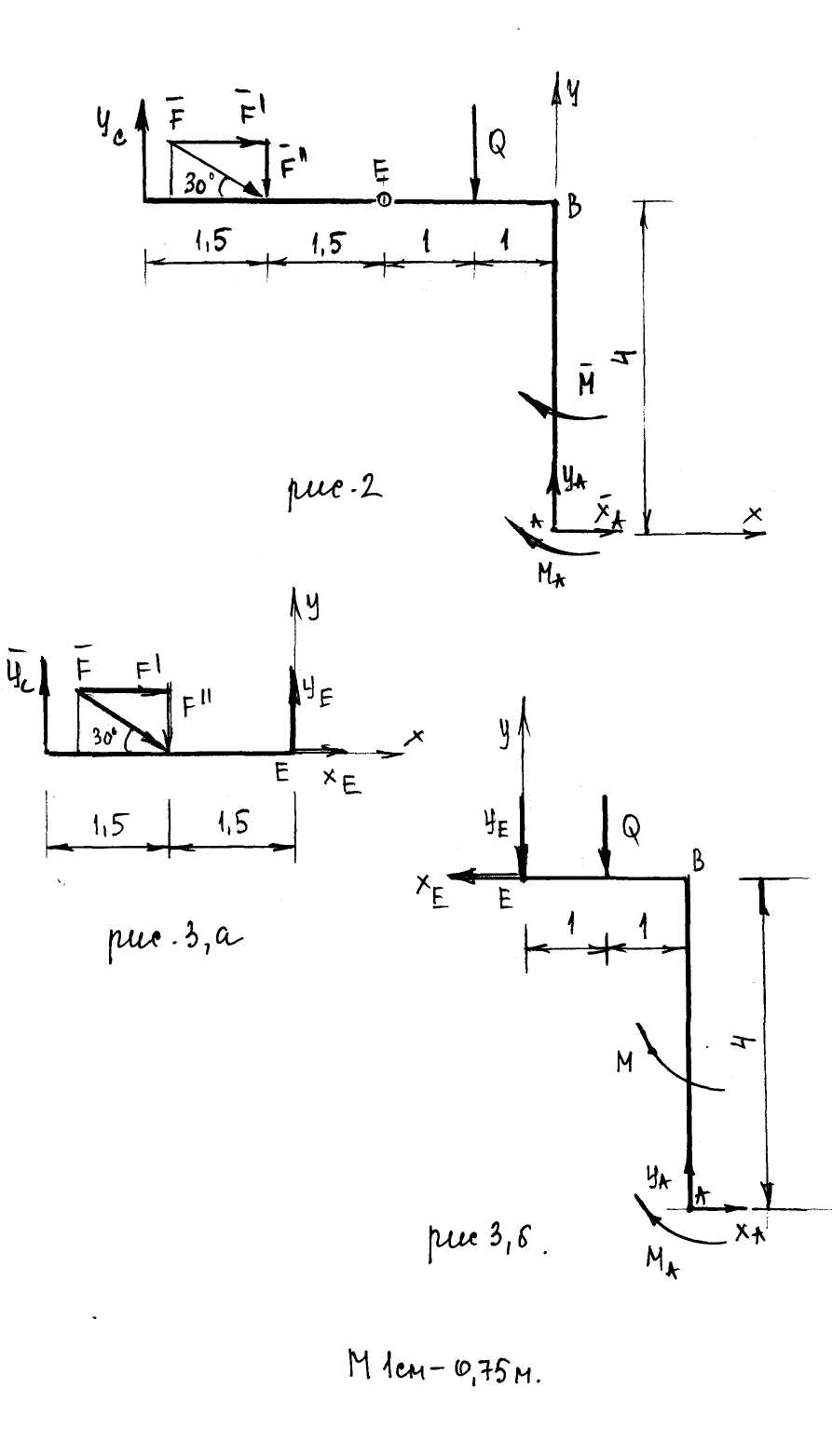C2-25

На вал с барабаном весом Qнамотана веревка, удерживающая груз весом Р, и насажено колесо радиусом rи весом G. Определить реакции подшипников А и В и момент М, приложенный к валу, в случае равновесия конструкции. Коэффициент трения f = 0,3

Схема конструкции приведена на рисунке 1. Числовые значения величин приведены в таблице 1.

P	G	Q	r	D		k	b	c	d
кН	кН	кН	м	м	град	м	м	м	М
12	0.085	0.75	0.45	0.22	-	0.4	0.65	0.3	0.6

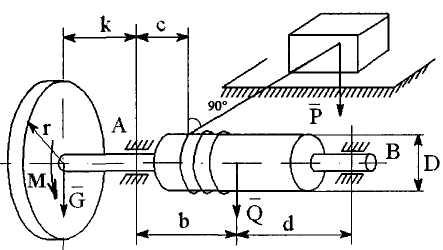рисунок 1.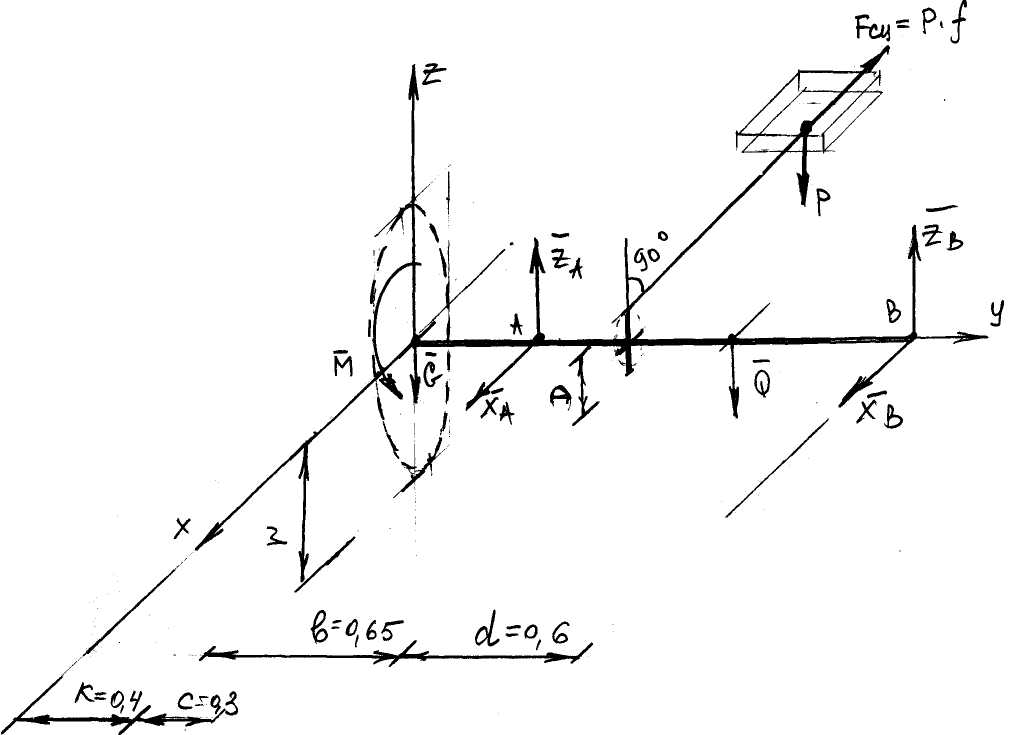





рисунок 2.

Решение. В рассматриваемой задаче при равномерном вращении вала действующие на него силы удовлетворяют условиям равновесия. Проведем координатные оси (рис. 2) и изобразим действующие на вал силы: натяжение веревки P, составляющие X_AZ_A X_BZ_B реакций подшипников, момент М, приложенный к валу, скольжение вала отсутствует. Коэффициент трения f=0,3.

Составляем уравнения равновесия.

ΣF_kX = 0; X_A +X_B - P·f =0 (1)

ΣF_kY=0; 0=0 (2)

ΣF_kZ=0; Z_A+ Z_B – G– Q -P = 0 (3)

Σ_X(F_k)=0; Z_A·k + Z_B(k+b+d) - Q(k+b) - P(k+c) =0 (4)

Σ_Y(F_k)=0; M – P · =0 (5)

Σ_Z(F_k)=0; -X_A·k – X_B(k+b+d) + P·f(k+c)=0 (6)

Подставим в уравнения все известные значения, уравнения примут вид:

X_A +X_B -12·0.3 =0 (1)

Z_A+ Z_B – 0.085– 0.75 -12 = 0 (3)

Z_A·0.4 + Z_B(0.4+0.65+0.6) – 0.75(0.4+0.65) - 12(0.4+0.3) =0 (4)

M – 12 · =0 (5)

-X_A·0.4 – X_B(0.4+0.65+0.6) + 12·0.3(0.4+0.3)=0 (6)

Из (5) M = 12· = 1.32 кНм

Из (1) X_A = - X_B + 12·0.3= -X_B+3.6

Из (6) – (-X_B+3.6)·0.4 – X_B(0.4+0.65+0.6) + 12·0.3(0.4+0.3)=0

Отсюда X_B = = 0,86кН; X_A = - 0,86 +3.6 = 2,74 кН

Из (3) Z_A = - Z_B + 12.84

Из (4)

(- Z_B +12.84)·0.4 + Z_B(0.4+0.65+0.6) – 0.75·(0.4+0.65 ) -12(0.4+0.3)=0

Отсюда Z_B= = 3.24 кН; Z_A = - 3.24 + 12.84 = 9.6 кН

X_A=2.74 кН; Z_A=9.6 кН; X_B=0.86 кН; Z_B=3.24 кН ; M=1.32 кНм